Погрешность или шумы квантования

При представлении аналового сигнала в квантованном виде возникают некоторые погрешности в представлении сигнала, который называют погрешностями.

Погрешности возникают по двум причинам.

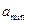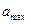1. Если у нас есть сигнал, то часто нам приходится отбрасывать самые малые значения от до и самые большие от 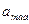до .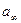

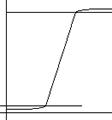Эти погрешности называют погрешностями ограничения сигнала.

Если сигнал изменяется случайно и может быть представлен плотностью вероятности

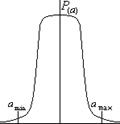
То погрешности 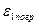может быть представлен как интеграл: 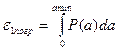(Первая граничная погрешность)

И 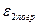будет представлен как интеграл: 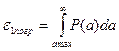(Вторая граничная погрешность)

И сумма погрешностей будет представлена из этих двух 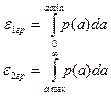как:

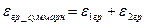
2. Эта погрешность возникает внутри диапазона квантования (шумы квантования).

Рассмотрим некий интеграл интервал квантования:

Мы наш сигнал величиной 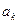должны представить неким уровнем 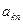– т.е. перевести на уровень квантования.

Погрешность у нас и будет той самой разницей между 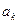и 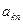; и величина 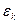тоже

Можно ввести меру отличия 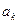от его квантованного значения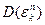

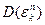тоже имеет вероятностное распределение и будет зависеть от плотности распределения вероятности самого сигнала - .

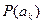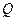- это точность представления.

Суммарная точность представления в этом интервале будет представляться как:

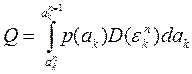
Суммарная погрешность будет равна: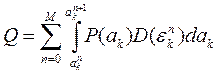

После преобразований можно получить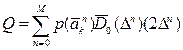

где 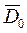- это средняя величина погрешности для каждого интервала квантования.

а 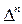- это ширина интервала квантования.

Погрешность квантования зависит от ширины интеграла квантования.

При квантовании систем нам необходимо выбрать интервал квантования.

Выбор интервала кантования по нескольким параметрам

1. Пороговый подход заключается в том что

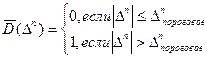
Выбранный критерий точности можно назвать критерием незаметности ошибки квантования т.е. при таком значении 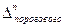нет перескока из одного интервала в другой.

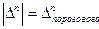(оптимизация решения задачи квантования) Ошибка будет незаметна.

Ширина n-го интервала квантования должна быть равна .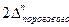

Представителем этого интервала квантования является величина 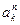, находящаяся в центре этого интервала квантования.

Если 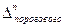не зависит от величины n, то получаем равномерную шкалу квантования ; при этом число уровней, т.е. интервалов квантования определяется соотношением:

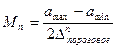где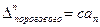

Для нас важно значение абсолютности ошибки, а не относительной.

Величина ошибки должна быть равномерна по логарифмическому закону.

Необходимо подвергать равномерному квантованию не саму величину а , её логарифмическое отношение: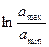

А число уровней квантования должно быть равно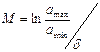

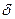- это визуальный порог восприятия человеческого глаза.

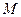- это число уровней квантования.

Визуальный порог восприятия человеческого глаза 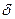должен быть равен 0,02.

т.е. если 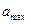=100

a 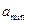=1, что соответствует 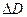= 2,0.

(По формуле 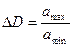). Отсюда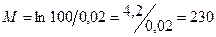

Отсюда мы имеем 230 уровней квантования. Это нужно, чтобы мы не видели погрешностей квантования, чтобы глаз не увидел шумов сигнала.

В соответствии с рассмотренным, мы получаем необходимое число уровней квантования для того, чтобы не различать дискретность квантования и воспринимать сигнал адекватный аналоговому необходимо иметь 230 уровней квантования. В технических системах , готовящих сигнал для визуального восприятия принято, что число таких уровней квантования должно быть не менее 256. 256 =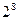

256 уровней являют собой промышленный стандарт.

Если наш стандарт меньше, то число градации и уровней квантования будет тоже восприниматься как аналоговый.