Кинетическая энергия одной частицы вращающего тела равна

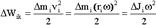Суммируя энергию частиц, получаем выражение для кинетической энергии вращающегося тела

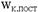Если тело одновременно участвует в поступательном и вращательном движении, то его кинетическая энергия равна сумме и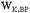

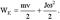 Момент инерции тела равен:
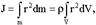где ρ - плотность тела. Тонкий однородный стержень длиной L (ось вращения на конце стержня): m1 = m 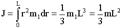L − масса на единицу длины,.

Тонкий однородный стержень длиной L (ось в центре): .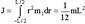

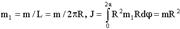Обруч (ось в центре):.

Пластина (ось в центре): m2 = m / ab,

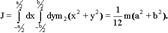
Кольцо (ось в центре): 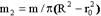− масса на единицу площади,

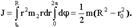
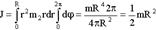Диск (ось в центре):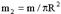

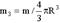Шар(ось в центре):,

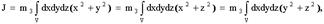
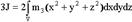сложив эти интегралы, получаем:, в сферической системе координат

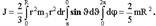
19. Колебания. Гармонический осциллятор.это колеб-я, движ-я (изменения состояния), обладающие той или иной степенью повторяемости. Свободные кол-я – к-я, кот-е происходят без внешнего воздействия, то есть был сообщён толчок, потом внешних сил нет (маятник). Вынужденные – в процессе кот-х воздействуют внешние период-ки изменяющиеся силы (люди по мсоту “в ногу”). Автокол-я – как вынужденные, но система сама управляет внешним воздествием (часы, в кот-х маятник поучает энергию за счёт поднятой гири). При параметрических кол-ях за счёт внешнего возде-я происходит период-е изм-е какого-либо парам-а системы (например: длина нити маятника). Осциллятор (качаюсь) – физ-я система, совершающая кол-я. Термин О. – мех система, совершающая колебания около положения устойчивого равновесия. В положении равновесия потенциальная энергия U системы имеет минимум. Если отклонения х от этого положения малы, то в разложении U (x) по степеням х можно считать U (x) = kx ²/2 (k — постоянный коэффициент); при этом квазиупругая сила F =- ∂U/∂x= -kx . Такие О. Наз-cя гармоническими, их движ-е опис-ся лин-ым ур-м , реш-е кот-го имеет вид х = A sin (wt + φ), где m — масса О., w=k/m – частота, А – амплитуда кол-й, φ — начальная фаза, t — время. Полная эн-я гарм-го О. Е = mw²А²/2 — это сумма период-ки меняющихся в противофазе кин-ой Т и пот-й U энергий; Е = Т + U не зависит от времени. Когда отклонение х нельзя считать малым, в разложении U (x) необх-м учёт членов более высокого порядка – ур-е движ-я становится нелинейным, а О. называется ангармоническим.

20. Мат-й маятник. Его период. М.м. – материал-я точка, совершающая под действием силы тяж-и кол-я вдоль дуги окр-ти, расположе-ой в верт-й плоскости. М.м: груз нерастяж-й нити, его размеры малы по сравнению с длиной нити, масса нити мала по сравн-ю с массой груза. Если отклонения М.м. малы, он совер-т кол-я, близкие к гарм-им, с периодом: T=2π*√(l/g).

21. Физич-й маятник. Его период.Если колеблющееся тело нельзя рассматривать как материальную точку, то М. называется физическим. Движение такого М. вполне аналогично движению кругового математического М. При малых углах отклонения j М. также совершает колебания, близкие к гармоническим, с периодом T=2π*√(l_пр/g), где l_пр =I/ml – приведённая длина – это длина физ-го маятника, преиод кол-й котого совпадает с периодом кол-й данного физ-го мая-ка, где I — момент инерции М. относительно оси подвеса, l — рассто-е от оси подвеса O до центра тяжести C, M — масса М.

22. Затухающие кол-я. Логарифмический декремент затухания.Затух-е кол-я – кол-я, у кот-х умен-ся интенсивность кол-й с теч-м времени, обусловленное потерей эн-ии колеб-ой системой (потеря эн-ии = превращение её в тепло вследствие трения в мех-х системах и сопрот-я в электр-х системах). Главным явл-ся случай, когда З. к. обусловлено уменьшением эн-ии, пропорц-ым квадрату скорости движ-я в мех-й системе (квадрату силы тока в электрической системе); это справедливо для линейных систем. Тогда З. к. имеет экспоненциальный характер, т. е. размахи кол-й убывают по зак. геом-ой прогрессии . Потери эн-ии в системе, вызывая З. к., нарушают их периодичность, значит затухающие кол-я не явл-ся период-м процессом (к ним неприменимо понятие периода или частоты). Но когда затухание мало, состояния в системе приблиз-о повтор-ся и можно пользоваться понятием периода как промежутка времени между двумя последующими прохождениями колеблющейся физической величины (тока, напряжения, размаха колебаний маятника) в одну и ту же сторону через макс-е знач-е. Оценку относительного уменьшения амплитуды колебаний за период даёт логарифмический декремент затухания – количеств-я характ-ка быстроты затухания кол-й. Д. з. δ равен натуральному логарифму отнош-я 2-х последующих макс-ых отклонений х колеблющейся величины в одну и ту же сторону: δ=ln(x₁/ x₂). Д. з. – величина, обратная числу кол-й, по истечении кот-х амплитуда убывает в е раз. Например, если δ = 0,01, то амплитуда умен-ся в е раз после 100 колебаний. Д. з. характеризует число периодов, в теч-е кот-х происходит затух-е кол-й, а не время такого затух-я. Полное время затухания определяется отношением Т/δ.

23.Вынужденные колебания. Зависимость амплитуды колебаний от частоты внешней силы. Резонанс. Резонансная частота.Колебания, совершающиеся под действием внешней периодической силы, называются вынужденными. Внешняя сила обеспечивает приток энергии к системе и не дает колебаниям затухать, несмотря на действие сил трения.

Особый интерес представляет случай, когда внешняя сила, изменяющаяся по гармоническому закону с частотой ω, воздействует на колебательную систему, способную совершать собственные колебания на некоторой частоте ω₀. Если собственные колебания происходят на частоте ω₀, которая определяется параметрами системы, то установившиеся вынужденные колебания всегда происходят на частоте ω внешней силы. После начала воздействия внешней силы на колебательную систему необходимо некоторое время Δt для установления вынужденных колебаний. Время установления по порядку величины равно времени затухания τ свободных колебаний в колебательной системе. Примером колебательной системы, способной совершать вынужденные колебания, может служить груз на пружине, свободный конец которой перемещается по гармоническому закону y=y₀cosωt. Если смещение груза от положения равновесия обозначить через х, то удлинение пружины Δl=x-y=x-y₀cosωt

Упругая сила F, действующая на груз, есть F=-k Δl=-kx+ky₀cosωt

Здесь k - коэффициент жесткости пружины. 2-ой закон Ньютона запишется в виде

x+ω₀²x=(ky₀cosωt)/m=ω₀²y0cosωt. Это уравнение называют уравнением вынужденных колебаний. Величина ω₀ есть собственная частота колебаний, ω - частота внешней силы.

Амплитуда x₀ вынужденных колебаний зависит от соотношения частот ω₀ и ω и от амплитуды вынуждающей силы ky₀. Если частота ω внешней силы приближается к собственной частоте колебаний ω₀, возникает резкое возрастание амплитуды вынужденных колебаний. Это явление называется резонансом. Зависимость амплитуды x₀ вынужденных колебаний от частоты ω вынуждающей силы называется резонансной характеристикой.

В отсутствие затухания амплитуда вынужденных колебаний при приближении к резонансу бесконечно растет. Однако в любой колебательной системе неизбежно присутствуют силы трения. Чем меньше трение в колебательной системе, тем сильнее возрастает амплитуда вынужденных колебаний при резонансе.