Отношение правдоподобия. Алгоритм обработки

Принятый одиночный сигнал можно рассматривать как функцию времени с известным законом модуляции, но неизвестными параметрами - временем запаздывания t_r, доплеровским сдвигом частоты F_дс , амплитудой E_с и фазой φ_c. Неопределённость относительно времени запаздывания и доплеровского сдвига частоты заставляет просматривать (одновременно или последовательно) все элементы разрешения по t_r и F_дс и принимать решения по каждому из них. Амплитуду и фазу принятого сигнала следует считать случайными, но постоянными на интервале, равном длительности сигнала T₀ , поскольку длительность одиночного сигнала, как правило, значительно мень­ше времени корреляции амплитудных и фазовых флуктуации принятого сигнала (T₀ << τ_с).

Представим одиночный сигнал в следующем виде:

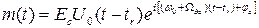
Помеху будем считать стационарным нормальным случайным процессом с комплексной огибающей N(t)

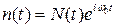
с нулевым средним значением

.

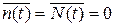Учитывая особенность задачи, обработки одиночных сигналов как задачи внутрипериодной обработки, можно воспользоваться единым представлением шумов и мешающих отражений, так как внутрипериодная структура мешающих отражений аналогична структуре шума: ширина спектра внутрипериодной структуры мешающих отражений опреде­ляется шириной спектра модуляции зондирующего сигнала. Поэтому в первом приближении и шум, и мешающие отражения в рассматриваемой задаче можно считать белым шумом со спектральной плотностью соответственно:

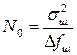- для шума,

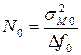- для мешающих отражений.

Значения сигнала и помехи в дискретные моменты времени t_g = g·Δt представить в виде:

,

.

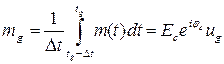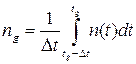При этом корреляционные свойства дискретных значений помехи, мешающей обнаружению одиночного сигнала, описываются символом Кронекера:

, .

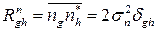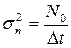Найдем отношение правдоподобия, определяющее структуру уст­ройства оптимальной обработки одиночного сигнала. Многомерная плотность вероятности дискретных значений входного сигнала f_g в отсутствие полезного сигнала (f_g = n_g) определяется выражением

,

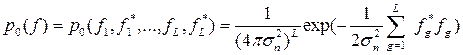где L = T₀/Δt - число дискретных значений за длительность одиночного сигнала.

При наличии полезного сигнала дискретные значения входного сигнала f(t) равны: f_g = m_g + n_g.

Учитывая, что полезный сигнал за время, равное его длительности, является известной функцией времени с постоянной амплитудой и фазой, можно утверждать, что наличие сигнала приводит лишь к смещению распределения величин f_g по сравнению со случаем, когда действует одна помеха, поскольку в этом случае n_g = f_g - m_g

.

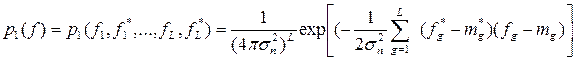Отношение правдоподобия принимает следующий вид:

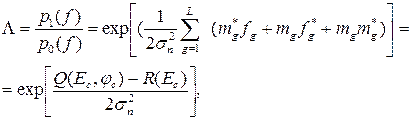
где

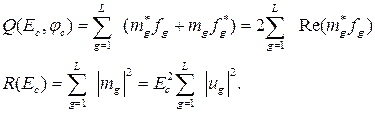
Величина R(E_c) от входного сигнала, т.е. от входной после­довательности f_g не зависит. Поэтому решение о наличии или отсутствии полезного сигнала можно принимать по величине Q(E_c, φ_c) зависящей от входного сигнала и монотонно связанной с отношением правдоподобия:

.

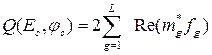Последнее выражение может служить алгоритмом обработки одиночного сигнала известной формы на фоне белого шума, из которого следует, что такая обработка в своей существенной части сводится к линейной обработке - весовому суммированию дискретных значений входного сигнала f_g, причем весовые коэффициенты m_g = m(t_g) определяются прообразом ожидаемого сигнала в анализируемом элемен­те разрешения - его формой или законом модуляции U₀(t), несущей частотой ω, временем запаздывания t_r, доплеровским сдвигом частоты F_дс, амплитудой E_с и начальной фазой φ_c. Ниже рассматриваются схемы корреляционных обнаружителей одиночного сигнала с различной степенью известности его параметров.