Виробництво роботи. корисна робота. максимальна робота. максимальна корисна робота

Якщо робоче тіло знаходиться в стані, відмінному від того, котрий воно має при параметрах навколишнього середовища (тобто система не знаходиться в рівновазі), то в принципі це робоче тіло може зробити роботу.

Ізольована система може зробити роботу тільки в тому випадку, коли вона не знаходиться в цілком рівноважному стані. Щоб ізольована система, єдиним видом роботи якої може бути робота розширення, могла зробити роботу, необхідно, щоб тиски або температури різних тіл, які входять у цю систему, не були абсолютно однакові.

У системі, яка складається з тіл з різними тисками, відсутня механічна рівновага. Якщо в системі маються тіла з різними температурами, то у ній відсутня термічна рівновага (теплова рівновага).

По мірі виробництва роботи, ізольована система буде наближатися до рівноважного стану. Допустимо, що ізольована система складається з навколишнього середовища, температура і тиск якої практично залишаються незмінними, і стиснутого повітря, що має ту ж температуру, що й навколишнє середовище, але більш високий тиск, тобто в наявності механічно нерівноважний і термічно рівноважний стани. Подібна система може робити роботу, наприклад, переміщаючи поршень у циліндрі доти, поки тиск повітря не знизиться до тиску навколишнього середовища, тобто поки система не прийде в механічну рівновагу.

Якщо в системі маються два джерела теплоти, які мають різні температури, і робоче тіло, початковий стан якого значення не має, то ми маємо справу з термодинамічною нерівноважною системою, що може зробити роботу, наприклад, шляхом кількаразового повторення робочим тілом циклу Карно. У результаті здійснення циклу Карно не тільки виявляється зроблена відома робота, але також цілком визначена кількість теплоти передається від джерела з більш високою температурою до джерела з більш низкою. Але в результаті такого переходу теплоти, температура гарячого джерела буде знижуватися, а холодного – підвищуватися. З часом температури джерел теплоти зробляться однаковим, система досягне термодинамічної рівноваги, і подальше виробництво роботи стане неможливим.

Таким чином, виробництво роботи ізольованою системою можливо тільки в процесі переходу системи з нерівноважного стану в рівноважний. Зроблена робота залежить, як відомо, від характеру процесу переходу системи до рівноважного стану. Отже, для добутку роботи далеко не байдуже яким шляхом система переходить з нерівноважного стану в рівноважний.

Допустимо знову, що в нашому розпорядженні мається термічно нерівноважна система, яка складається з двох джерел теплоти, що мають різні температури і робочі тіла. Теплота передається безпосередньо від гарячого джерела до холодного, минаючи робоче тіло. У результаті такого процесу, температури усіх тіл системи стануть однаковими, система виявиться в стані термічної рівноваги, а ніякої роботи узагалі не буде зроблено. Подібний процес теплообміну, (який приводить до вирівнювання температур) без виробництва роботи обов'язково повинний відбуватися при кінцевій різниці температур, тобто необоротньо.

Навпаки, максимальна робота при переході системи від термічно нерівноважного стану в рівноважний може бути отримана в результаті кількаразового здійснення робочим тілом циклу Карно, у якому найбільша температура робочого тіла дорівнює температурі гарячого джерела, а найменша температура – температурі холодного джерела, тобто в результаті здійснення тільки цілком оборотних процесів.

Якщо ізольована система механічно нерівноважна, то в цьому випадку найбільша робота, яку можна одержати при переході з механічно нерівноважного стану в рівноважний, може бути отримана в результаті здійснення цілком оборотних процесів. Представимо, що робота виробляється за допомогою поршневої повітряної машини. Ясно, що найбільша робота буде отримана у випадку відсутності тертя між поршнем і стінками циліндра машини. Але тертя являє собою типовий необоротний процес.

Таким чином, ми прийшли до двох дуже важливих висновків:

1. Ізольована система здатна до виробництва роботи тільки у випадку, коли вона знаходиться в нерівноважному стані. Після досягнення рівноважного стану працездатність системи виявляється вичерпаною.

2. Для одержання найбільшої можливої роботи при переході системи з нерівноважного стану в рівноважний, потрібно, щоб усі процеси, які протікають у системі, були цілком оборотні.

Визначимо тепер більш чітко поняття корисної роботи, максимальної роботи і максимальної корисної роботи, яка може бути зроблена розглянутою системою. Спробуємо чисельно визначити максимальну корисну роботу, яку може зробити система, чи, як іноді говорять, визначимо працездатність системи. У нашому розпорядженні мається ізольована система, яка складається з навколишнього середовища і деякого тіла або сукупності тіл, які мають відмінні від середовища тиск р і температуру Т (чи один з цих параметрів). Таке тіло або групу тіл будемо називати надалі джерелом роботи.

У нерівноважній ізольованій системі робота виробляється при зміні стану джерела роботи в процесі встановлення рівноваги в цій системі. Позначимо цю роботу L. Частина цієї роботи буде затрачатися на стиснення навколишнього середовища. Так як система ізольована, то її об’єм є постійним, тому збільшення його (розширення) на величину 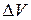у процесі встановлення рівноваги в системі може відбуватися тільки за рахунок зменшення на ту ж величину 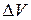об’єму навколишнього середовища.

Роботу, витрачену на стиснення навколишнього середовища (проти сил тиску середовища р₀), позначимо L₀.

Оскільки частина роботи, виробленої в процесі встановлення рівноваги в ізольованій системі, завжди буде затрачатися на стиснення навколишнього середовища, то, отже, використовувати за своїм розсудом ми можемо не всю зроблену роботу L, а тільки ту її частину, що залишається за винятком L₀. Цю частину зробленої роботи умовимося називати корисною роботою. L_кор = L – L_0, (7.1)

Як уже відзначалося, якщо перехід системи з нерівноважного стану в рівноважний здійснюється за допомогою оборотних процесів, то в цьому випадку система зробить найбільшу можливу в даних умовах роботу (тобто зроблена робота буде максимальною). Так як усі реальні процеси виявляються в більшому чи в меншому ступені необоротними, то максимальна робота системи є недосяжною межею. Однак для порівняння ступеня досконалості процесів одержання роботи, поняття про подібну межу виявляється корисним. Максимальну роботу системи позначимо L_макс.Максимальна кориснаробота – 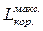, що може зробити система (працездатність системи) – це, за аналогією з рівнянням (7.1), частина максимальної роботи, за винятком роботи, затрачуваної на стиск навколишнього середовища: 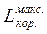= L_макс – L₀, (7.2)

Визначимо 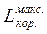. Допустимо, що температура Т₀ і тиск р₀ навколишнього середовища незмінні. Початкові параметри джерела роботи: p, V, T, U, S, Н. Кінцеві параметри джерела роботи: p_к, V_к, T_к, U_к, S_к, Н_к. Кінцеві параметри навколишнього середовища: p_0к, V_0к, T_0к, U_0к, S_0к, Н_0к. Причому р_к = р₀ і Т_к = Т₀.

Сумарна внутрішня енергія системи в початковому, нерівноважному стані:

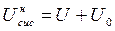, (7.3)

Сумарна внутрішня енергія системи в кінцевому рівноважному стані

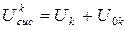, (7.4)

Так як розглянута система по визначенню є ізольованою ( 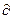q_сис.=0), то з рівняння 1-го закону ТТД випливає, що робота може бути зроблена системою тільки за рахунок зменшення її внутрішньої енергії: 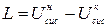, (7.5)

З обліком (7.3) і (7.4) одержуємо: L = (U + U₀) – (U_k + U_0k) = (U – U_k) + (U₀ – U_0k), (7.6)

Але між джерелом роботи і навколишнім середовищем може існувати теплообмін, крім того, джерело роботи може робити роботу над середовищем (проти тиску середовища). Позначимо Q₂ - теплоту, передану джерелом роботи середовищу, а L₀ – роботу, зроблену джерелом роботи над середовищем. Відповідно до 1-го закону ТТД: U_0k – U₀=Q₂+L₀ , (7.7)

Так як тиск середовища р₀ за умовою незмінний, то: L₀ = p₀ (V_к – V) , (7.8)

Оскільки розглянута система є ізольованою, її сумарний об’єм постійний і, отже, зміна об’єму однієї частини цієї системи-середовища дорівнює по величині (і протилежно за знаком) зміні об’єму іншої її частини – джерела роботи. Тому в рівнянні (7.8) для L₀ – робота стиснення навколишнього середовища – фігурує зміна об’єму джерела роботи V_к – V, а не навколишнього середовища V₀ – V_к.

Тоді, змінюючи знак у (7.7) і підставляючи L₀ з (7.8), отримаємо:

U₀ – U_0к = - Q₂ – p₀ (V_к – V) , (7.9)

Підставляючи значення U₀ – U_0к з рівняння (7.9) у (7.6), отримаємо:

L = (U – U_к) – Q₂ – p₀ (V_к – V) , (7.10)

Теплота, передана від джерела роботи навколишньому середовищу, дорівнює, очевидно, добутку незмінної температури середовища Т₀ і збільшенню ентропії середовища (S_0к – S₀), тобто: Q₂ = T₀ (S_0k – S₀), (7.11)

Підставляючи значення Q₂ з рівняння (7.11) у рівняння (7.10), отримаємо:

L = (U – Uк) – Т₀ (S_0k – S₀) – p₀ (V_к – V), (7.12)

Рівняння (7.12) дає значення корисної роботи, яка зроблена ізольованою системою при переході з нерівноважного стану в рівноважний. Тому що з усієї зробленої роботи віднімається частина її p₀(Vk – V), яка витрачена на стиск навколишнього середовища і, отже, не може бути використана по нашому розсуді.

Для того, щоб знайти максимальну корисну роботу (працездатність) ізольованої системи, необхідно скористатися положенням про те, що в результаті протікання оборотних процесів ентропія ізольованої системи не змінюється. Звідси випливає, з обліком адитивності ентропії, що якщо ентропія джерела роботи зменшувалася на S – Sк, то ентропія середовища повинна зрости на те ж значення, тобто для оборотних процесів: S_0к – S₀ = S – S_к , (7.13)

Підставляючи (7.13) у (7.12) одержимо вираження для максимальної корисної роботи ізольованої системи: 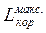= (U – U_к) – T₀ (S – S_к) – p₀ (V_к – V), (7.14)

Як видно з (7.14), максимальна корисна робота системи однозначно визначається початковими параметрами джерела роботи і параметрами навколишнього середовища.

7.2. Поняття про ексергію. Рівняння Гюі-Стодоли

Термін «ексергія» у 1956р. увів югославський учений З.Рант і утворений він із грецьких коренів «екс» - зовнішній і «ерг» - робота, дія.

Максимальну корисну роботу (працездатність) у сучасної ТТД прийнято називати ексергією. У даному випадку величина 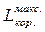- це ексергія джерела роботи, що знаходиться в об’ємі V і позначається Е_V.

У таким чином: Е_V = (U – Uк) – T₀ (S – Sк) – p₀ (Vк – V), (7.15)

Звідси випливає, що якщо параметри навколишнього середовища задані, то ексергію можна розглядати як функцію стану робочого тіла.

За аналогією з поняттям про максимальну корисну роботу ізольованої системи (працездатності) вводиться поняття про працездатність теплоти.

Якщо в ізольованій системі, яка складається з двох джерел теплоти з температурою Т₁ і Т₂ (Т₁>T₂) і робочого тіла, гаряче джерело віддає q₁ теплоти, то максимальна робота, яка може бути отримана від цієї теплоти, являє собою роботу оборотного циклу Карно, здійснюваного в інтервалі температурТ₁ – Т₂. На практиці намагаються забезпечить рівність Т₂ = Т₀.

Отже, під працездатністю теплоти, яка зветься ексергією теплоти е_q розуміється максимальна корисна робота, яку можливо отримати від теплоти q₁ при температурі гарячого джерела Т₁ за умови, що холодне джерело теплоти знаходиться в термічній рівновазі з навколишнім середовищем, Т = Т₀, тобто:

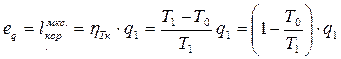, (7.16)

де 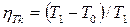- термічний ККД циклу Карно.

Підкреслимо ще раз, що ексергія це – максимальна можлива корисна робота, яку може зробити ізольована система, якщо процеси, що ведуть до встановлення рівноваги в цій системі, будуть протікати оборотньо (працездатність системи). А L_кор – це робота, яку може зробити та ж система у випадку необоротності процесів, що протікають у ній. Різниця цих величин являє собою втрату ексергії (працездатності) системи внаслідок необоротності процесів, що протікають у ній.

L_кор – 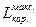= (U₂ – U₁) –T₀ (S_0к– S₀) – p₀ (V–V_к) – (U₂– U₁) + T₀(S – S_к) + p₀ (V – V_к) =

= T₀ (S – S_к) – (S_0к – S₀) = 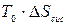, де 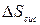- зміна ентропії системи.

Як відомо: 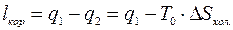, (7.17)

Ентропія гарячого джерела теплоти зменшується, тому що це джерело теплоту віддає, а ентропія холодного джерела збільшується. Так як при оборотності всіх процесів, що протікають в ізольованій системі, сумарна ентропія цієї системи не змінюється, то збільшення ентропії холодного джерела теплоти ∆S_хол повинно дорівнювати зменшенню ентропії гарячого джерела ∆S_{гар .}

Оскільки оборотність усіх процесів, які протікають в ізольованій системі, відповідає випадку одержання 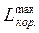- ексергії теплоти е_q, то для цього випадку з обліком ∆S_гор= ∆S_хол., одержуємо з (7.17): 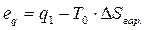, (7.18)

З рівняння (7.18) і (7.17) випливає: 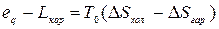, (7.19)

Оскільки, як уже відзначалося, ентропія робочого тіла в циклі не змінюється, то очевидно, що різниця величин 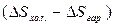являє собою зміну ентропії всієї розглянутої ізольованої системи. 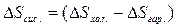, (7.20)

З урахуванням цього співвідношення одержуємо з (7.17) рівняння для втрати ексергії теплоти внаслідок необоротності процесів, що протікають у розглянутій ізольованій системі в наступному виді: 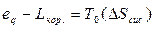, (7.21)

Це рівняння зветься рівнянням Гюі-Стодоли по імені французького фізика М. Гюі, який уперше вивів це рівняння в 1889 році, і словацького теплотехніка А. Стодоли, який вперше застосував це рівняння для рішення технічних задач. Це рівняння знаходить широке застосування при аналізі ефективності роботи теплових установок.

Рівняння Гюі-Стодоли розкриває фізичний зміст ентропії. Виявляється, що необоротні процеси переходу теплоти з більш високого на більш низький температурний рівень супроводжуються втратою працездатності, тобто деградацією енергії тієї системи, у якій вони відбуваються, а відповідне зростання ентропії пропорційно цій утраті працездатності.

Утрату ексергії позначають D – дисипація – розсіювання енергії, тобто:

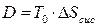, (7.22)

Таким чином, ентропію можна розглядати як параметр стану замкнутої системи, збільшення якого є кількісною мірою втрати працездатності системи, що має місце при протіканні в ній необоротних процесів.

ЛЕКЦІЯ 9