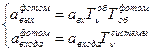Фурье-преобразование непериодической функции

Непериодическая функция не может быть представлена в ряде Фурье, однако она допускает анализ-Фурье с использованием интеграла Фурье. Также непериодическая функция допускает разложение по Фурье – т. е. с представлением в виде с синусоидальным преобразованием; но это разложение проводиться в виде интеграла.

Для одномерной непериодической функции интеграл Фурье будет иметь следующий вид:

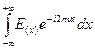; причем выражение может быть записано в виде функции 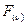; т. е.: . И тогда наше выражениеи можно записать как .

Для четной функции мы можем представить выражение более просто:

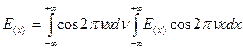
Или в упрощенной форме:

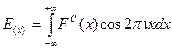
Фурье-преобразование для непериодической функции уже не имеет дискретного спектра. Этот спектр уже имеет сплошную функцию типа:

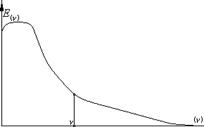
Функция также представляется суммой синусоидальных составляющих, бесконечно близких по частоте и их спектральная плотность амплитуд – это амплитуда, отнесенная к единице полосы пространственных частот.

Рассмотрим пример преобразования непериодической функции. В качестве преобразования Фурье возьмем П-образный сигнал.

Отсюда берем интеграл:

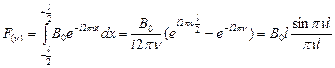
Вид этой функции будет иметь вид:

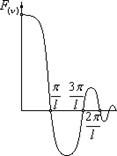
Эта функция будет иметь название SINC.

Для дельта-функции спектр будет равен единице при любой частоте.

Функция передачи модуляции системы.

Возьмем объект, имеющий синусоидальное распределение интенсивности; то есть, синусоиду (в случае, когда как на картинке – косинусоида):

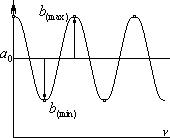
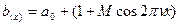
Модуляция 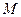- это отношение:

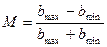
Или по такой формуле:

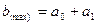
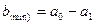
Подставляя это все в формулу модуляции, получаем:

Отсюда имеем:

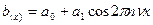
А теперь рассмотрим нашу решетку в системе светорассеяния; то есть в системе функции размытия линии.

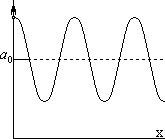
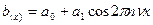
Возьмем интеграл свертки: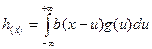

И подставляем в него выражение .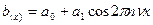

Получаем: .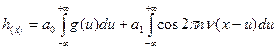

А используя выражение 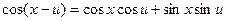, получаем:

.

Принимаем интеграл функции размытия линии за единицу и получаем:

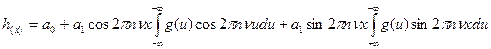
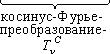
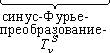
Отсюда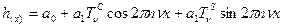

Исходя из геометрии:

имеем:

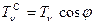
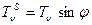
или

отсюда выражение 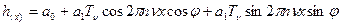переходит в

.

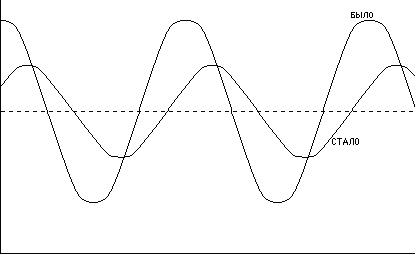
Было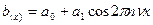

Стало .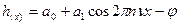

1.Функция осталась синусоидальной; осталась постоянная и та же частота. Изменилось амплитуда решетки, и появился угол 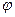, который называется углом фазового сдвига.

Итак, у нас изменяется амплитуда и появляется угол фазового сдвига 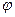. Поэтому у функции 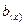, представляющей собой синусоидальную решетку уменьшается амплитуда и появляется сдвиг; но только в том случае, если .

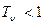Совокупность характеристик 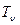и называются частотной характеристикой системы, т. е. характеристикой системы по ее размытию, выраженной в частотном пространстве. При этом 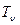– это Фурье-преобразование функции размытия линии. Если функция размытия является симметричной – у нее отсутствует фазовый сдвиг; то она называется амплитудной частотной характеристикой.

Фазово-частотная характеристика – это зависимость угла сдвига фазы называется от пространственной частоты.

Если увеличивается пространственная частота, то амплитудно-частотная характеристика уменьшается, а фазовая частотная характеристика – наоборот – возрастает.

Если система имеет симметричную зону размытия, то есть, четная функция, то фазово-частотная характеристика отсутствует, а остается амплитудно-частотная модуляция.

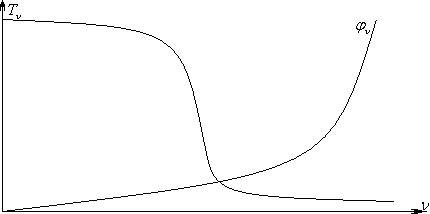
Функция передачи модуляции характеризует систему с точки зрения размытия узких пучков и является эквивалентной функции размытия линии или краевой функции; прямо с ними связана путем Фурье-преобразования. Т. е. ФПМ есть косинус Фурье-преобразование функции размытия линии. Отличие только в том, что

Переведена в частотное пространство.

Сама функция передачи модуляции – это зависимость передачи коэффициента передачи модуляции от пространственной частоты.

Т. е.

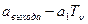
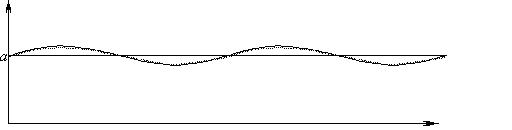
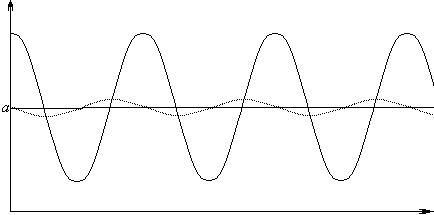
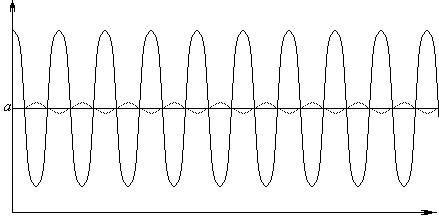
Функция передачи модуляции является фильтром пространственных частот, так как низкие частоты она пропускает, а высокие частоты – нет.

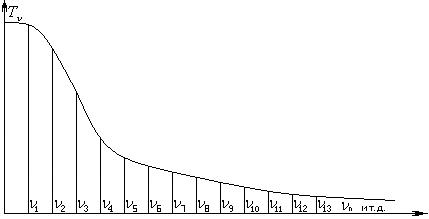
При низкой пространственной частоте амплитуда сигнала существенно не изменяется, но при ее увеличении амплитуда уменьшается, приближаясь к нулю(равномерное распределение освещенности), то есть, решетка исчезает.

Неудобство ФРТ и ФРЛ состоит в том, что их трудно измерить. Другое неудобство состоит в том, что нужно каждый раз решать интеграл свертки.

Краевая функция (knife age)

Функцию передачи модуляции можно оценивать путем отношения амплитуды сигнала на выходе к амплитуде сигнала на входе или амплитуды изображения к амплитуде объекта:

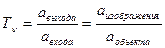
Для измерения этой функции передачи модуляции нужно взять несколько решеток с разной пространственной частотой. И по ним находим дискретные точки.

Можно сделать так: берем все амплитуды, при чем 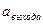самой широкой амплитуды приравниваем к единице; а остальные подгоняем под нее.

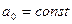
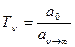
Все эти измерения ФПМ можно перевести в одномерную форму. А именно – методом сканирования наше пространственное изображение мы переводим в серию электрических сигналов; а затем, измеряя эти сигналы на вольтметре, получая пиковые значения амплитуд, считаем их.

Радиальная мира (несинусоидальная).

Преимущества использования функции передачи модуляции.

1. Может разлагаться в ряд Фурье.
2. При перемещении от периферии к центру будет меняться пространственная частота.
3. Если система у нас состоит из нескольких звеньев и все эти звенья линейные, то ФПМ можно найти простым перемножением отдельных звеньев ФПМ.

Например, если у нас имеется фотоаппарат и мы знаем 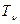объектива и 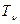пленки; то систему мы получим:

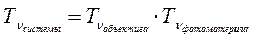
А именно: 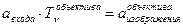. Затем: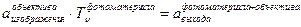

Или так: