Общее (временное) ур-ние Шредингера

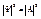
Явный вид Y-ф-ции для микрочастицы:

Y-ф-ция, описывающая движение микрочастиц в различных уровнях, будет иметь явный вид.

Любой волновой процесс описывается с помощью уравнения:

(1) ...

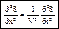
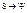
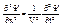- НЕВОЗМОЖНО!

Для нахождения Y-ф-ции взять простое волновое ур-ние и заменить в нём S на Y нельзя, т.к.:

1) Y-ф-ция из (1) не удовлетворяет принципу суперпозиции;

2) решение ур-ния (1) соответствует реальным процессам, в которых комплексная часть отбрасывается.

В 1926 Шредингер записал полностью удовлетворяющее всем св-вам ур-ние:

(2) ...

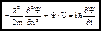
общее временное уравнение Шредингера для одномерного случая движения частицы с массой m. 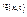. U(x,t) - силовая потенциальная функция. Зависит от координаты и времени. Для трёхмерного случая (2) переходит в:

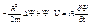... (2’)

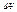- оператор Лапласса.

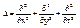
С помощью (2) и (2’) можно описать вероятность перехода эл-на на новые стационарные орбиты.

Знание Y-ф-ции позволяет находить квадрат модуля Y-ф-ции - интенсивность волны де Бройля.

Условия решения (2) и (2’):

1) Должна быть известна U(t)

2) Должна быть известна Y(x,0) или Y(x,y,z,0)

3) Граничные условия - знание поведения микрочастицы на границе: Y(0,t);Y(l,t)

4) Решением (2) и (2’) является Y-ф-ция, для которой справедливыстандартные условия:

a) НЕПРЕРЫВНА;

б) ОДНОЗНАЧНА;

в) КОНЕЧНА.

Непрерывна - потому чтовероятность нахождения микрочастицы от точки к точке скачком меняться не может.

Однознаяна - не может быть 2-х значений вероятности.

Конечна - соответствует условию нормировки (чтобы был интеграл).

Ур-ние Шред. для стацион. состояния.

Для нахождения y(x,y,z) из (2) и (2’) необходимо составить ур-ние без времени. Сделаем переход от (2), испольуя возможность замены Y(x,t) на j(t) и y(x).

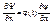
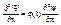
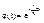
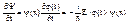
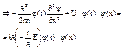
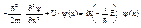
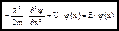... (1)

стационарное уравнение Шредингера.

E - полная энергия; U(x) - потенциальная энергия, m - масса. y - ?.

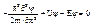
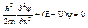
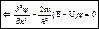... (1’) - Для одномерного случая. EU=T.

y(x,y,z), U(x,y,z) Þ

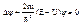
D - оператор Лапласса

.

Задание17

Частица в одномерном потенциальном ящике.

Рассмотрим вначале идеализированную потенциальную яму с бесконечно высокими стенками, называемую потенциальным ящиком. Потенциальный ящик задается рельефом, который аналитически и графически предстает в следующем виде: 0 при 0 £ х

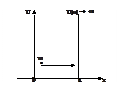
U(х) =∞ при х < 0 и х > а где а - ширина ямы (ящика).

Внутри ящика потенциальная энергия частицы равна нулю, а вне его - бесконечности, поэтому частица, помещенная в ящик, выйти из него не сможет. Это соответствует условию j(х) = 0 при 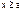и .

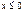Уравнение Шредингера для стационарных состояний 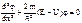применяем только для области 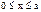, т. е. внутри ящика, где потенциальная энергия равна нулю. Вне ящика 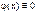, то есть, частицы там нет. Итак, при U = 0: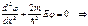 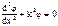, где k = Ö(2mЕ/ 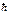²) - волновое число. Определим решение этого уравнения для частицы в ящике.

В ящике движение частицы является ограниченным, и волновая функция частицы не может выражаться бегущей волной. Вернее, здесь надо брать суперпозицию двух бегущих в противоположные стороны волн, которые в итоге дают стоячую волну .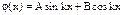

Из граничного условия j(0) = 0 следует: j(0) = В = 0 и тогда 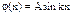. Из условия на другой границе j(а) = 0 Þ j(а) = А sin kа = 0 Þ kа = np, где n = 1, 2, 3, … Отсюда и проистекает квантование волнового числа k = np/а, а с ним и импульса р = 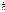k, и энергии Е частицы в ящике:

.

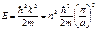Эта формула выражает спектр собственных значений энергии частицы в ящике.

Квантование энергии является результатом ограничения (локализации) движения микрочастицы. Условие k = np/а есть условие «стоячести» волны де Бройля частицы в ящике, при котором на длине (ширине) а ящика должно укладываться целое число n полуволн l/2 волновой функции частицы: k = 2p/l = np/а Þ а = nl/2.

Расстояние между соседними энергетическими уровнями частицы в ящике равно:

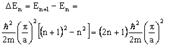
В отличие от атома водорода, в потенциальном ящике энергетические уровни не сгущаются с ростом их номера n, а разрежаются.

Разность между соседними энергетическими уровнями обратно пропорциональна массе частицы и квадрату ширины ящика: DЕ_n ~ 1/m и DЕ_n ~ 1/а².Таким образом, квантовый характер энергетического спектра движущейся частицы усиливается с уменьшением ее массы и с локализованностью (ограниченностью в пространстве) ее движения (с уменьшением а).

Относительное расстояние между энергетическими уровнями DЕ_n/Е_n = (2n + 1)/n² ~ 1/n убывает с ростом номера энергетического уровня. При больших значениях квантового числа n, определяющего номер и величину энергетического уровня, дискретность энергии нивелируется (энергия уровня растет быстрее, чем интервал между ними). Это означает фактически переход к классической физике; здесь "работает" принцип соответствия - при больших квантовых числах эффекты квантования нивелируются, и движение приобретает классические черты, отражаемые классической механикой. Квантованность нивелируется и при а ® ¥. Спектр энергии частицы становится при этом непрерывным, что соответствует переходу к свободной частице.

Волновая функция частицы в ящике 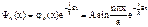оказывается различной на разных энергетических уровнях. Множитель А определяется из условия нормировк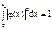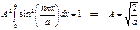и:

и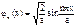

n = 1;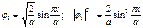

n = 2;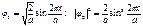

n = 3;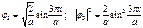

На длине (ширине) ящика а укладывается целое число длин полуволн 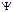- функции (условие "стоячести" волны).

В нижнем энергетическом состоянии (n = 1), называемом основным, частица с большей вероятностью находится в центре ящика. При n = 2, наоборот, частица в центре ящика находиться не может, ибо там плотность вероятности |j(а/2)|² = 0.

С ростом квантового числа n возрастает число равновероятных мест пребывания частицы в ящике. При n ® ¥ волновая функция осциллирует столь часто, что максимумы практически сливаются, и частица равновероятно находится в любой точке ящика: имеем, согласно принципу соответствия, переход от квантовой к классической механике.

Задание18

Потенциальный барьер бесконечной ширины E>U.

Потенциальным барьером называют потенциальный рельеф в виде ступеньки.

1. E > U_о (низкий потенциальный барьер). Микрочастица, имеющая кинетическую энергию большую высоты барьера, может, как пролететь над ступенькой во вторую область (с вероятностью D), так и отразиться от нее (с вероятностью R). Эта возможность отражения от низкого барьера (потенциальной ступеньки), выражает принципиальное отличие квантовой частицы от классической. Классическая частица при Е > U_о барьер всегда преодолевала. Для квантовой (микро -) частицы условие Е > U_о может нарушаться в силу соотношения неопределенности для энергии (DЕ × Dt ³ 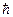) и на короткое время Dt превращаться в свою противоположность Е £ U_о.

Прошедшая за барьер частица уменьшает свою кинетическую энергию и импульс, что соответствует увеличению длины волны (волновой функции): l₂ > l₁. Это следует и из формул для волновых чисел:

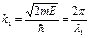и 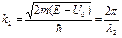Þ l₂ > l₁.

Изобразим на графике характер волновых функций частицы на фоне потенциального рельефа ступеньки (чтобы не загромождать чертеж, изображаем только бегущие - падающую и проходящие волны).

Задание19

Потенциальный барьер бесконечной ширины E<U

Потенциальным барьером называют потенциальный рельеф в виде ступеньки.

2. Случай с E < U_о (высокий потенциальный барьер). Налетающая на барьер частица имеет энергию меньшую высоты барьера. Как и в первом случае, на

ступеньке скачком меняется амплитуда и длина волны (волновой функции), полная же энергия, в силу консервативности системы, должна оставаться непрерывной.

Т. к. при Е < U_о, 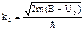- мнимое,
то есть k₂ = ik, то 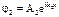= А₂ 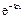- не волна, а затухающая экспонента.

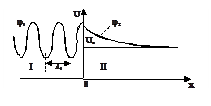
Плотность вероятности нахождения частицы во 2 -ой области 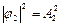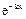- экспоненциально убывает с ростом х, т. е. с удалением от границы барьера. Как это понимать? Проникает частица во вторую область или нет? Считается, что частица может заходить во вторую область, но затем обязана вернуться обратно. Частица не уходит совсем во вторую область, но и отражение ее от ступеньки происходит не

на самой границе барьера, а с определенной (убывающей) вероятностью смещено от границы во вторую область. Объяснение этой возможности проникновения частицы за высокий потенциальный барьер также, как и отражение от низкого барьера, может быть связано с привлечением соотношения неопределенности Гейзенберга для энергии DЕ ×Dt ³ 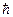. На коротких интервалах Dt времени неопределенность DЕ энергии может быть достаточной для перехода условия Е < U_о в условие Е > U_о, которое и позволяет частице заходить за границу барьера.

Коэффициент отражения R частицы от высокого потенциального барьера бесконечной ширины всегда равен единице, а коэффициент пропускания D = 0.

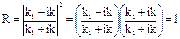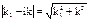( и )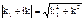

D = 1 – R = 0.

Задание20.

Гармонический осциллятор.

Движение осуществляется под действием квазиупругой силы.

F= - cx, md²x/dt² + cx=0

x’’+cx/m = 0

ω₀² = c/m

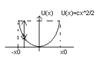
Если частица двигается (возбужд сост), то вероятность обнаружить её в пределах от x до x+dx определяется временем dt нахождения частицы

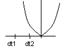
dt₂<dt₁, W₂<W₁

W~1/υ – плотность вероятностей обнаружить частицу пр-ва обратно пропорционально υà0, Wà∞

Полная энергия частицы не изменяется, но в зависимости от величины x0 (от степени возбуждения) может иметь непрерывный ряд значений.

Квантовая частица (одномерный случай)

∂²Ψ/∂x² + 2m[E-U(x)] Ψ/ћ² = 0

Частица находится в потенциальном поле, на неё действует квазиупругая сила.

U(x)=cx²/2, c=mω₀²

U(x)= mω₀²x²/2

∂²Ψ/∂x² + 2m[E- (mω₀²x²/2)] Ψ/ћ² = 0

Решение этого уравнения позволяет определить собственные ф-ии Ψn(x) и собств значения энергии. Из решения следует, что квантовый гармонический осциллятор может принимать только дискретные значения эн-ии.

{{Для потенциал ящика:

E_n=n² ћ²(π/l)²/2m

Ψ_n(x)=√(2/l)*sin(nπx/l)}}

E_n=(1/2 + n)ћω₀, n=0,1,2… - квантовое число

Квантовый гармонич осциллятор не имеет нулевого значения энергии

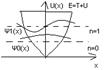
Wкв=|Ψ|²

n=0

E_n=E₀= ћω₀²/2

Ψ₀(x)~ exp(-x²/2x²) / x^1/2

ω₀(x)= exp(-x²/x₀²) / x

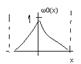
Вероятность обнаружить квант частицу max но в отличие от классич, частицу можно обнаружить в любом другом месте и даже за пределами амплитуды x0

Вероятность обнаружить микрочастицу min при x=0 и max в 2-х координатах.

С увеличением квант числа число «горбов» увеличивается. Результирующая кривая может быть описана непрерывной ф-ией U(x).

.
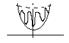