Временное и стационарное уравнение Шрёдингера
Де Бройль сопоставил свободно движущейся частице плоскую волну:
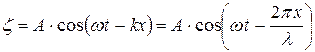
Заменив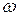 
и 
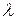на р и Е 
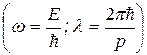получим
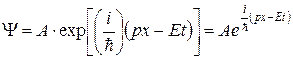
Функцию Y называют волновой функцией или амплитудой вероятности (по Борну). Она может быть комплексной, и вероятность W пропорциональна квадрату ее модуля. Таким образом, описание состояния микрообъекта с помощью волновой функции имеет статистический характер: квадрат модуля волновой функции определяет вероятность нахождения частицы в момент времени t в пределах объема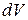 
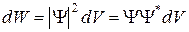(3)
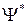- функция комплексно сопряженная Y. Величина
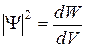имеет смысл плотности вероятности, т.е. определяет вероятность нахождения частицы в единичном объеме в окрестностях точки с координатами x, y, z. Таким образом, физический смысл имеет не сама Y-функция, а квадрат ее модуля, которым задается интенсивность волн де Бройля.
Вероятность найти частицу в момент времени t в конечном объеме:
.
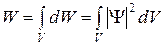Так как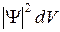 
определяется как вероятность, то необходимо волновую функцию нормировать так, чтобы вероятность достоверного события обращалась в единицу, если за объем V принять бесконечный объем всего пространства. Это означает, что при данном условии частица должна находиться где-то в пространстве. Условие нормировки:
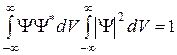. (4)
На Y-функцию налагают стандартные условия: она должна быть непрерывной, однозначной, конечной, иметь непрерывные и конечные первые производные.
Таким образом, квантовая механика носит статистический характер, она лишь определяет вероятность нахождения частицы в данной точке пространства.
Волновая функция является решением уравнения Шредингера, полученного им в 1926 г. Уравнение Шредингера, как и все основные уравнения физики, не выводится, а постулируется. Правильность этого уравнения подтверждается согласием с опытом получаемых результатов. Общий вид его:
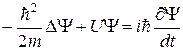(5)
m – масса частицы, U – потенциальная энергия частицы, D - оператор Лапласа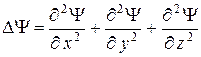 
, i – мнимая единица, Y - искомая волновая функция.
Можно прийти к уравнению Шредингера следующим образом. Рассмотрим свободно движущуюся частицу вдоль оси Х (U = 0):
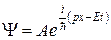
Тогда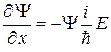 
; 
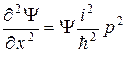
Выразив Е и р2, получим:
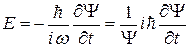
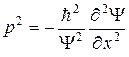
Учтя, что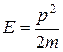 
, получим
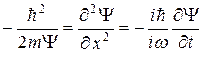
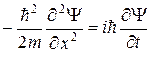совпадает с (7.7) при U = 0
Если силовое поле, в котором движется частица, является стационарным (U не зависит от t) то волновую функцию можно представить в виде произведения двух функций, одна из которых есть функция только координат, другая – только времени:
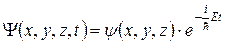
При подстановке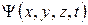 
во временное уравнение Шредингера (5) и после сокращения на 
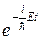придем к уравнению Шредингера для стационарных состояний
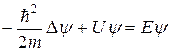
или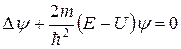 
(6)
Уравнение (6) называется уравнением Шредингера для стационарных состояний. Решениями этого уравнения будут функции, имеющие место лишь при определенных значениях параметра E (за счет налагаемых на волновую функцию требований). Эти значения энергии называются собственными. Решения же, которые соответствуют собственным значениям энергии, называются собственными функциями. Совокупность собственных значений энергии образует спектр, который может быть как дискретным, так и непрерывным.