Т е м а 12-13. ПОЛЯРИЗАЦИЯ ВЕЩЕСТВА. ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ

12.1. Вычислить поляризуемость 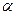для модели молекулы “металлический шарик”.

12.2. Вычислить поляризуемость 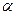для модели молекулы “пудинг с изюмом”.

12.3. Вычислить поляризуемость 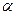для планетарной модели Бора-Резерфорда.

12.4. Небольшая сфера радиусом а и поляризуемостью 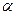расположена на очень большом расстоянии от сферы радиусом b, изготовленной из проводящего материала, которая поддерживается при потенциале U. Найдите приближенное выражение для силы, действующей на сферу из диэлектрика, справедливое при условии а<<r, где r-расстояние между сферами.

12.5. Вывести соотношение Клаузиуса-Моссотти, связывающее диэлектрическую постоянную 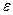с поляризуемостью среды .

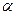13.1. Плоский конденсатор состоит из 2-х параллельных слоев различных веществ. Первый слой толщиной d имеет диэлектрическую проницаемость 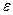и электропроводность, равную нулю; для другого слоя толщиной kd диэлектрическая проницаемость 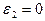, а электропроводность 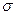имеет конечное значение. Показать, что в отношении распространения монохроматических плоских волн этот конденсатор ведет себя так, как если бы все пространство между пластинами было заполнено однородной средой с диэлектрической проницаемостью .

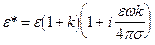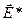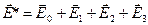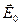13.2.* При расчете электрического поля, действующего на отдельную молекулу в диэлектрике, вокруг рассматриваемой молекулы строят сферу, радиус которой по сравнению с расстояниями между молекулами, при этом указанная сфера не должа пересекать ни одной молекулы. Тогда поле , действующее на молекулу, находящуюся в центре сферы, можно представить в виде суммы полей , где -электрическое поле внешних по отношению к диэлектрику источников, 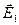-поле, обусловленное связанными зарядами, появившимися в результате поляризации на внешней поверхности диэлектрика, 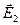-поле связанных зарядов, находящихся на внутренней поверхности диэлектрика, 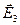-поле всех молекул, находящихся внутри сферы. Поле 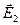впервые было вычислено Лоренцом (формула Лорентц-Лоренца) 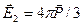, где 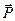-вектор поляризации.

Однако полость внутри диэлектрика не обязательно выбирать в виде сферы: ее можно, например, выбрать в виде куба с гранями, соответственно нормальными и параллельными вектору поляризации. В этом случае плотность связанных зарядов на верхней и нижней гранях куба постоянна и равна 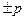, в то время как на других гранях связанные заряды отсутствуют. Вычислить величину поля 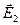для кубической полости.

13.3. В некоторых случаях функцию 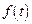, определяющую связь между 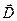и :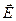

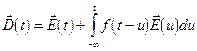
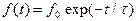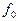можно представить в виде , где и 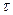-постоянные. Показать, что при этом

,

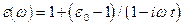где 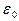-статическое значение диэлектрической проницаемости.

13.4. Исходя из условия причинности, согласно которому поляризация в среде может возникнуть только после начала действия электрического поля, доказать, что вещественная и мнимая части диэлектрической проницаемости

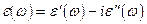
связаны между собой формулами:

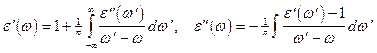
(соотношения Крамерса-Кронига).

Символом 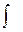обозначено главное значение интеграла.

Указание: рассмотреть поляризацию 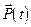, возникающую в сфере под действием поля 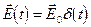. Воспользоваться формулой

,

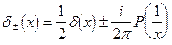так что 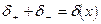— дельта-функция Дирака. Символ Р представляет главное значение.

13.5. С помощью дисперсионных соотношений Крамерса-Кронига (см. задачу 13.4.) определить вещественную часть диэлектрической проницаемости 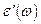по известной мнимой части :

,

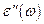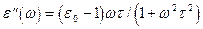где 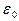и 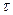-постоянные.

13.6. Доказать следующие правила сумм для мнимых частей диэлектрической проницаемости:

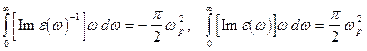
где 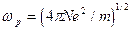-плазменная частота.

Указание: обратить внимание на то, что 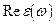является четной, а 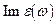-нечетной функциями от 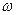на вещественной оси, и воспользоваться асимптотическим выражением 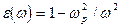, справедливым при 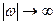всюду в верхней полуплоскости .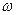