Импульс тела. Закон сохранения импульса в природе и технике

Простые наблюдения и опыты доказывают, что покой и движение относительны, скорость тела зави­сит от выбора системы отсчета; по второму закону Ньютона, независимо от того, находилось ли тело в покое или двигалось, изменение скорости его движе­ния может происходить только при действии силы, т. е. в результате взаимодействия с другими телами. Однако существуют величины, которые могут сохра­няться при взаимодействии тел. Такими величинами являются энергия и импульс.

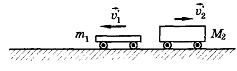
Импульсом тела называют векторную физи­ческую величину, являющуюся количественной ха­рактеристикой поступательного движения тел. Им­пульс обозначается р. Единица измерения импульса Р — кг • м/с. Импульс тела равен произведению мас­сы тела на его скорость: р = mv. Направление векто­ра импульса р совпадает с направлением вектора скорости тела v (рис. 4).

Для импульса тел выполняется закон сохране­ния, который справедлив только для замкнутых фи­зических систем. В общем случае замкнутой назы­вают систему, которая не обменивается энергией и массой с телами и полями, не входящими в нее. В механикезамкнутой называют систему, на кото­рую не действуют внешние силы или действие этих сил скомпенсировано. В этом случае р₁ = р₂ где р₁ — начальный импульс системы, а р₂ — конеч­ный. В случае двух тел, входящих в систему, это вы­ражение имеет вид m₁v₁ + т₂v₂ = m₁v₁' + т₂v₂' где т₁ и т₂ — массы тел, а v₁ и v₂, — скорости до взаимодей­ствия, v₁' иv₂' — скорости после взаимодействия. Эта формула и является математическим выражением закона сохранения импульса:импульс замкнутой физической системы сохраняется при любых вза­имодействиях, происходящих внутри этой системы.

Другими словами: в замкнутой физической системе геометрическая сумма импульсов тел до взаимодействия равна геометрической сумме импульсов этих тел после взаимодействия. В случае незамкнутой системы импульс тел системы не сохраняется. Одна­ко, если в системе существует направление, по кото­рому внешние силы не действуют или их действие скомпенсировано, то сохраняется проекция импульса на это направление. Кроме того, если время взаимо­действия мало (выстрел, взрыв, удар), то за это время даже в случае незамкнутой системы внешние силы незначительно изменяют импульсы взаимодействую­щих тел. Поэтому для практических расчетов в этом случае тоже можно применять закон сохранения им­пульса.

Экспериментальные исследования взаимодей­ствий различных тел — от планет и звезд до атомов и элементарных частиц — показали, что в любой си­стеме взаимодействующих тел при отсутствии дей­ствия со стороны других тел, не входящих в систему или равенстве нулю суммы действующих сил, гео­метрическая сумма импульсов тел действительно остается неизменной.

В механике закон сохранения импульса и за­коны Ньютона связаны между собой. Если на тело массой т в течение времени t действует сила и ско­рость его движения изменяется от v₀ до v, то уско­рение движения a тела равно a = (v - v₀)/t. На осно­вании второго закона Ньютона для силы F можно записать F = та = m(v - v₀)/t, отсюда следует Ft = mv - mv₀.

Ft — векторная физическая величина, харак­теризующая действие на тело силы за некоторый промежуток времени и равная произведению силы на время t ее действия, называетсяимпульсом силы.

Единица импульсав СИ — Н • с.

Закон сохранения импульса лежит в основе реактивного движения.Реактивное движение — это такое движение тела, которое возникает после отде­ления от тела его части.

Пусть тело массой т покоилось. От тела отде­лилась какая-то его часть т₁ со скоростью v₁. Тогда оставшаяся часть придет в движение в противопо­ложную сторону со скоростью v₂, масса оставшейся части т₂ Действительно, сумма импульсов обоих частей тела до отделения была равна нулю и после разделения будет равна нулю:

т₁v₁ +m₂v₂ = 0, отсюда v₁ = -m₂v₂/m₁.

Технические идеи Циолковского нахо­дят применение при создании современной ракетно-космической техники. Движение с помощью реак­тивной струи, по закону сохранения импульса, ле­жит в основе гидрореактивного двигателя. В основе движения многих морских моллюсков (осьминогов, медуз, кальмаров, каракатиц) также лежит реактив­ный принцип.

Билет№4