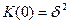Шумы и помехи в изображении

Шумы – это возникающие в изображении различного рода нарушения его целостности, структуры, которые являются нежелательными и ухудшают его качества.

Шумы могут быть случайными (стохастическими) и детерминированными.

Случайные возникают на первой стадии формирования изображения – как оригинала, так и обработки этого сигнала, когда он еще представлен в аналоговой форме.

Эти шумы могут быть разделены на две группы: шумы аналоговые и импульсные шумы.

Детерминированные шумы – это шумы, которые возникают при обработке компьютерной системой нашего изображения. Детерминированные шумы в свою очередь бывают – пространственной дискретизации и шумы квантования.

Случайные шумы проявляются еще в аналоговом изображении, еще на фотографическом материале.

При нормальном изменении оптической плотности, мы будем иметь вид нашей кривой:

А при микро фотометрии мы можем увидеть такие вот флуктуации:

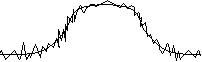
Случайные шумы могут появляться и во время сканирования.

Также, на фоне непрерывно меняющегося сигнала могут быть импульсные выбросы – шумы.

- царапины

- пылинки

- грязь.

Случайное распределение оптической плотности и есть зернистость.

Случайный аналоговый шум возникает в любых системах.

Описание случайного аналогового шума

1. Невозможно предсказать текущее значение, которое принято в текущей точке пространства или текущий момент времени, в который принят данный сигнал.
2. Можно только оценить на определенной длине вероятность появления текущего значения.

Кривая плотности вероятности

1

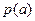
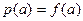
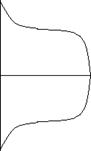- нормальная кривая распределения, выражается, Гауссовской величиной.

Случайный шум можно охарактеризовать

1. Средним значением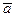

2. Квадрат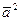

3. Первым и вторым начальными распределениям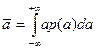и: и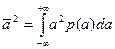

Есть функция симметричная, то величина шума не изменяет среднего значения сигнала т.е. первый начальный момент равен нулю.

Ширина кривой плотности распределения вероятности – это кривая, которая может быть описана с помощью второго центрального момента распределения или дисперсии:

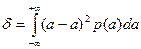
Дисперсия

Корень квадратный из дисперсии - 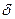- это среднее квадратичное отклонение, которое тоже является важнейшей характеристикой шума.

Шум характеризуется не только величиной отношения, но также и частотными параметрами

2

Частотные свойства функции характеризуются функцией автокорреляции.

Функция автокорреляции.

Возьмём решётку – непрозрачные штрихи на не прозрачном фоне. Ширины просветов по размерам равны штрихам: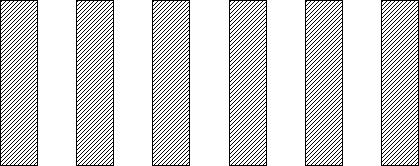

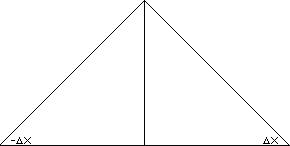
Освещённость после прохождения света уменьш на 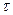0.5

=0,5

Представим, что у нас есть две таких решётки и будем эту решётку совмещать с первой решёткой. Если штрихи и просветы сложим, то всё так и останется 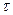=0,5.

Теперь мы вторую решётку смещаем на расстояние 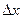вправо. Это приведёт к тому что ширина просвета у нас сузится на 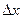, а штрих увеличится на .

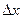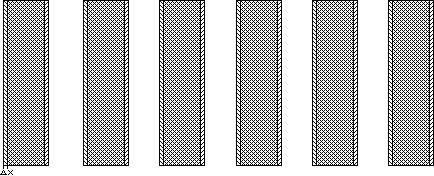
Ещё сместим на 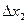- ещё расширится на это же расстояние. В конце концов, мы можем сместить так, что штрихи все закроют:

Для широкой решётки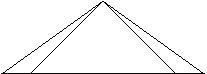

Чем грубее решётка, тем

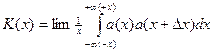
Для первой будет шире, а для второй уже.

Чем крупнее шум, тем будет шире функция автокорелляции.

Можно также записать как