Классический расчет теплоемкости идеальной кристаллической решетки. Закон Дюлонга и Пти.
Задача о равновесной внутренней энергии и, соответственно, о теплоемкости идеальной кристаллической решетки сводится к задаче о теплоемкости равновесной системы независимых линейных гармонических осцилляторов с единичной массой, т.е. к задаче о равновесной системе с гамильтонианом
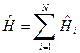 , (1)
, (1)
где
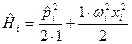 (2)
(2)
- оператор Гамильтона линейного гармонического осциллятора с единичной массой и частотой 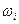 ,
,
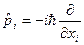 - оператор обобщенного импульса, отвечающий обобщенной координате
- оператор обобщенного импульса, отвечающий обобщенной координате 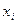 . Здесь
. Здесь 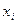 - не обычная декартовая координата, а некоторая обобщенная координата. Как видно,
- не обычная декартовая координата, а некоторая обобщенная координата. Как видно, 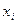 не имеет даже размерность длины.
не имеет даже размерность длины.
Каждый осциллятор отвечает одному из собственных колебаний кристаллической решетки. Различные осцилляторы отвечают различным собственным колебаниям. Каждому собственному колебанию отвечает свой собственный осциллятор. 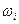 есть частота соответствующего собственного колебания кристаллической решетки.
есть частота соответствующего собственного колебания кристаллической решетки.
Собственное колебание кристаллической решетки представляет собой бегущую по кристаллу плоскую волну смещений атомов. Произвольное колебание кристаллической решетки можно представить в виде суперпозиции этих плоских волн – собственных колебаний. Каждое собственное колебание задается двумя величинами – квазиволновым вектором 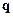 , или квазиимпульсом
, или квазиимпульсом 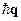 , и номом зоны
, и номом зоны 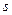 , или зонным индексом.
, или зонным индексом.
Квазиволновой вектор 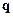 определяет изменение фазы колебаний атомов при переходе из одной элементарной ячейки кристаллической решетки к другой, т.е. квазиволновой вектор
определяет изменение фазы колебаний атомов при переходе из одной элементарной ячейки кристаллической решетки к другой, т.е. квазиволновой вектор 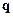 определяет направление распространения плоской волны смещений атомов в собственном колебании. Номер ветви
определяет направление распространения плоской волны смещений атомов в собственном колебании. Номер ветви 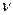 нумерует различные типы собственных колебаний с одним и тем же квазиволновым вектором. Например, это могут быть продольные колебания, когда атомы смещаются вдоль направления квазиволнового вектора. Это могут быть поперечные колебания, когда атомы смещаются в направлении, перпендикулярном квазиволновому вектору и т.д. Вообще говоря, каждому значению квазиволнового вектора отвечает
нумерует различные типы собственных колебаний с одним и тем же квазиволновым вектором. Например, это могут быть продольные колебания, когда атомы смещаются вдоль направления квазиволнового вектора. Это могут быть поперечные колебания, когда атомы смещаются в направлении, перпендикулярном квазиволновому вектору и т.д. Вообще говоря, каждому значению квазиволнового вектора отвечает 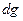 различных собственных колебаний. Здесь
различных собственных колебаний. Здесь 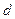 - размерность кристаллической решетки.
- размерность кристаллической решетки. 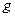 - число атомов в элементарной ячейке.
- число атомов в элементарной ячейке.
Квазиволновой вектор обладает особенностью, существенно его отличающей от волнового вектора обычных волн в сплошной среде. Не все значения квазиволнового вектора являются физичиски различными. Два значения квазиволнового вектора 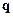 и
и 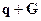 , отличающихся на вектор обратной решетки, являются физически эквивалентными. Это означает, что этим двум волновым векторам, отличающимся на вектор обратной решетки, отвечают одинаковые собственные колебания. Непрерывная область
, отличающихся на вектор обратной решетки, являются физически эквивалентными. Это означает, что этим двум волновым векторам, отличающимся на вектор обратной решетки, отвечают одинаковые собственные колебания. Непрерывная область 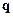 -пространства, содержащая в себе все физически различные значения квазиволного вектора, называется зоной Бриллюэна. Ясно, что квазиволновой вектор имеет смысл рассматривать в пределах первой зоны Бриллюэна. В дальнейшем мы будем рассматривать квазиволновой вектор в пределах первой зоны Бриллюэна. Первая зона Бриллюэна определяется тремя неравенствами
-пространства, содержащая в себе все физически различные значения квазиволного вектора, называется зоной Бриллюэна. Ясно, что квазиволновой вектор имеет смысл рассматривать в пределах первой зоны Бриллюэна. В дальнейшем мы будем рассматривать квазиволновой вектор в пределах первой зоны Бриллюэна. Первая зона Бриллюэна определяется тремя неравенствами
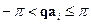 , i=1,2,3. (3)
, i=1,2,3. (3)
Здесь 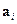 - векторы элементарных трансляций кристаллической решетки. У трехмерной решетки три вектора элементарной трансляции.
- векторы элементарных трансляций кристаллической решетки. У трехмерной решетки три вектора элементарной трансляции.
Как уже говорилось, каждому значению квазиволнового вектора отвечает 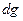 различных собственных колебаний, с вообще говоря, различными частотами. Возьмем некоторое значение квазиволнового вектора
различных собственных колебаний, с вообще говоря, различными частотами. Возьмем некоторое значение квазиволнового вектора 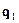 . Этому значению отвечает
. Этому значению отвечает 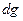 различных собственных колебаний с, вообще говоря, различными частотам. Пронумеруем эти частоты натуральным индексом
различных собственных колебаний с, вообще говоря, различными частотам. Пронумеруем эти частоты натуральным индексом 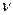 в порядке возрастания. Самому маленькому значению частоты припишем индекс 1, следующему по величине – индекс 2 и т.д. Берем другое значение квазиволнового вектора. Точно также нумеруем с помощью натурального индекса
в порядке возрастания. Самому маленькому значению частоты припишем индекс 1, следующему по величине – индекс 2 и т.д. Берем другое значение квазиволнового вектора. Точно также нумеруем с помощью натурального индекса 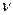 частоты соответствующих собственных колебаний в порядке возрастания и т.д. до тех пор, пока не переберем все значения квазиволнового вектора в пределах первой зоны Бриллюэна. Если мы теперь будем рассматривать частоты и амплитуды собственных колебаний с данным значением индекса
частоты соответствующих собственных колебаний в порядке возрастания и т.д. до тех пор, пока не переберем все значения квазиволнового вектора в пределах первой зоны Бриллюэна. Если мы теперь будем рассматривать частоты и амплитуды собственных колебаний с данным значением индекса 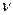 как функцию квазиволнового вектора, непрерывно изменяющегося в пределах первой зоны Бриллюэна, то мы получим гладкие и непрерывные кривые. По этой причине множество все собственных колебаний с данным значением
как функцию квазиволнового вектора, непрерывно изменяющегося в пределах первой зоны Бриллюэна, то мы получим гладкие и непрерывные кривые. По этой причине множество все собственных колебаний с данным значением 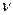 называется
называется 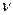 -ой ветвью собственных колебаний. Зависимость частоты собственных колебаний
-ой ветвью собственных колебаний. Зависимость частоты собственных колебаний 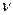 -ой ветви от квазиволнового вектора называется законом дисперсии этой ветви.
-ой ветви от квазиволнового вектора называется законом дисперсии этой ветви.
Напомню, что различают два типа ветвей собственных колебаний – акустические и оптические ветви. В трехмерном кристалле число акустических ветвей равно 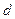 . Соответственно, число оптических ветвей
. Соответственно, число оптических ветвей 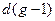 .
.
В акустических ветвях закон дисперсии
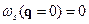 . (4)
. (4)
При малых 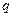 (
( 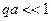 ) закон дисперсии акустических ветвей носит звуковой характер.
) закон дисперсии акустических ветвей носит звуковой характер.
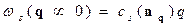 , (5)
, (5)
где
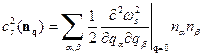 , (6)
, (6)
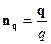 . (7)
. (7)
Такой закон дисперсии обусловлен тем, что в колебаниях акустических ветвей при длинных волнах все атомы в элементарной ячейке смещаются практически одинаково, т.е. элементарная ячейка колеблется как целое. Сложная структура ячейки при этом не проявляется. Акустическим ветвям обычно приписывают индексы 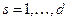 .
.
В оптических ветвях напротив
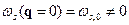 . (8)
. (8)
Соответственно, при малых 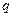 (
( 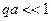 ) закон дисперсии имеет вид
) закон дисперсии имеет вид
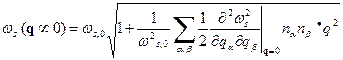 , (9)
, (9)
Такой закон дисперсии обусловлен тем, что в колебаниях оптических ветвей при длинных волнах положение центра тяжести элементарной ячейки практически не меняется, т.е. ячейка деформируется. Оптическим ветвям обычно приписывают индексы 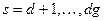 .
.
Любой кристалл, вообще говоря, имеет конечные размеры. Когда мы описываем кристалл, мы должны задать граничные условия. Граничные условия призваны описывать физическую ситуацию на поверхности кристалла. Однако, все известные в природе силы достаточно быстро убывают с расстоянием. Поэтому в глубине кристалла явления на поверхности практически не будут ощущаться. Нас интересуют аддитивные величины. Значение аддитивной величины для всей системы равно сумме ее значений для частей этой системы. Поскольку объем кристалла, в котором практически не ощущается его поверхность, существенно превышает прилегающий к границе объем, для которого граница, существенна, то конкретный вид граничных условий практически не влияет на значение аддитивной величины. Влияние граничных условий определяется отношение объема, для которого граница существенна, к объему, в котором граница не ощущается. В нашем случае объемного кристалла с макроскопическими размерами это отношение мало. Поэтому в нашем случае использование тех или иных граничных условий, по большому счету, вопрос удобства. По той же самой причины, понятно, форму кристалла можно брать такую, какая удобна. При этом, конечно граничные условия и форма кристалла должны быть разумными – не какими-нибудь экзотическими. В нашем случае очень удобно рассматривать наш кристалл. В нашем случае кристалл удобно рассматривать как параллелипипед, построенный на векторах элементарных трансляций кристаллической решетки и ставить периодические граничные условия, т.е. требовать, чтобы на противоположных гранях этого параллелепипеда все было одинаково. Наложение этих граничных условий приводит к тому, что спектр квазиволнового вектора является дискретным . Проекция квазиволнового вектора на направление вектора элементарной трансляции 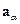
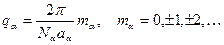 , (10)
, (10)
где 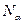 - число элементарных ячеек, помещающихся в элементарный объем в данном направлении.
- число элементарных ячеек, помещающихся в элементарный объем в данном направлении.
Подставляя (10) в условия (3), получаем
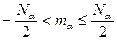 . (11)
. (11)
Таким образом, число физически различных значений квазиволнового вектора равно числу элементарных ячеек 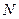 в основном объеме. Соответственно, полное число собственных колебаний равно
в основном объеме. Соответственно, полное число собственных колебаний равно 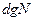 . Кроме того, как мы знаем, квазинепрерывный характер спектра квазиволнового вектора позволяет в дальнейшем суммы по квазиволновому вектору заменять интегралами
. Кроме того, как мы знаем, квазинепрерывный характер спектра квазиволнового вектора позволяет в дальнейшем суммы по квазиволновому вектору заменять интегралами
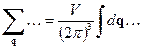 . (12)
. (12)
Итак, задача о внутренней энергии иделальной кристаллической решетки сводится к расчету теплоемкости равновесной системы 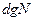 независимых линейных гармонических осцилляторов с единичной массой.
независимых линейных гармонических осцилляторов с единичной массой.
Задача о равновесной системе линейных была решена на практическом занятии. Поэтому, воспользовавшись известным результатом, получаем, что свободная и внутренняя энергия кристаллической решетки есть
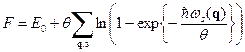 , (23)
, (23)
и
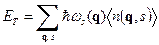 . (24)
. (24)
где
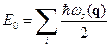 (25)
(25)
- энергия нулевых колебаний,
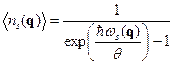 , (26)
, (26)
- среднее значение числа осциллятора, отвечающего собственному колебанию s-ой ветви с квазиволновым вектором 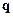 (среднее число квантов энергии, запасенных этим осциллятором).
(среднее число квантов энергии, запасенных этим осциллятором).
Этот результат можно интерпретировать на языке квазичастиц. Будем каждому осциллятору, т.е. каждому собственному колебанию, поставим в соответствие квазичастицу с энергией, равной кванту этого осциллятора. Такие квазичастицы называются фононами. Каждый фонон задается двумя квантовыми числами- 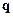 и
и 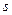 . Фононы отвечающие оптическим ветвям называются оптическими. Фононы отвечающие акустическим ветвям называются акустическими. Поставим нашей системе осцилляторов газ таких фононов так, чтобы число фононов данного типа в газе соответствовало числу заполнения соотв.етствующего осциллятора. Если система осцилляторов переходит из одного состояния в другое, т.е. меняются числа заполнения осцилляторов, то соответствующее число фононов рождается и исчезает. Тогда
. Фононы отвечающие оптическим ветвям называются оптическими. Фононы отвечающие акустическим ветвям называются акустическими. Поставим нашей системе осцилляторов газ таких фононов так, чтобы число фононов данного типа в газе соответствовало числу заполнения соотв.етствующего осциллятора. Если система осцилляторов переходит из одного состояния в другое, т.е. меняются числа заполнения осцилляторов, то соответствующее число фононов рождается и исчезает. Тогда 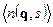 можно интерпретировать как среднее число фононов в газе, а (23) и (24) представляет собой внутреннюю энергию фононного газа. Таким образом, вместо кристаллической решетки можно рассматривать бозе-газ – газ фононов.
можно интерпретировать как среднее число фононов в газе, а (23) и (24) представляет собой внутреннюю энергию фононного газа. Таким образом, вместо кристаллической решетки можно рассматривать бозе-газ – газ фононов.
Как обсуждалось выше, спектр квазиволнового вектора формально является дискретным. Однако расстояние между соседними значениями квазиволнового вектора очень мало - обратно пропорционально размеру кристалла. Это позволяет в выражении (36) заменить сумму по квазиволновым векторам на интеграл
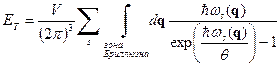 . (27)
. (27)
Рассмотрим случай низких температур, малых настолько, что в выражении для 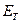 можно учитывать только звуковые колебания акустических ветвей.
можно учитывать только звуковые колебания акустических ветвей.
Установим, что это за низкие температуры. В знаменателе подынтегрального выражения стоит экспонента. Поэтому подынтегральное выражение быстро стремиться к нулю с ростом отношения 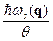 . Следовательно, определяющий вклад в
. Следовательно, определяющий вклад в 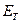 дают колебания с частотами
дают колебания с частотами 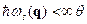 . Остальными колебаниями можно с большой точностью пренебречь. Нам нужно установить, при каких температурах этому условию удовлетворяют только звуковые колебания акустических ветвей. Длина звуковой волны связана с частотой как
. Остальными колебаниями можно с большой точностью пренебречь. Нам нужно установить, при каких температурах этому условию удовлетворяют только звуковые колебания акустических ветвей. Длина звуковой волны связана с частотой как 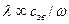 . В звуковых волнах длина волны
. В звуковых волнах длина волны 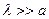 , и соответственно
, и соответственно 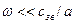 . Следовательно, в тепловом вкладе во внутреннюю энергию кристаллической решетки можно учитывать только звуковые колебания акустических ветвей при температурах
. Следовательно, в тепловом вкладе во внутреннюю энергию кристаллической решетки можно учитывать только звуковые колебания акустических ветвей при температурах
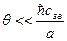 . (28)
. (28)
Закон дисперсии в звуковых колебаниях акустических ветвей имеет вид (5). Заметим, что скорость звука, вообще говоря, зависит от направления квазиволнового вектора. Давайте сделаем еще одно стандартное упрощение – заменим реальную скорость звука на ее среднее значения по направлению квазиволнового вектора. Обозначения менять не будем. В дальнейшем под 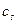 будем понимать среднюю по
будем понимать среднюю по 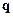 .
.
В знаменателе подынтегрального выражения стоит экспонента. Поэтому подынтегральное выражение быстро стремиться к нулю с ростом отношения 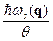 . Следовательно, мы можем подставить в интеграл закон дисперсии закон дисперсии и распространить интегрирование на все
. Следовательно, мы можем подставить в интеграл закон дисперсии закон дисперсии и распространить интегрирование на все 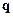 -пространство. При этом мы, конечно, ошибемся, однако при низких температурах эта ошибка будет незначительной. Из-за экспоненты в знаменателе вклад областей, в которые мы неправомерно залезем, будет мал. Таким образом,
-пространство. При этом мы, конечно, ошибемся, однако при низких температурах эта ошибка будет незначительной. Из-за экспоненты в знаменателе вклад областей, в которые мы неправомерно залезем, будет мал. Таким образом,
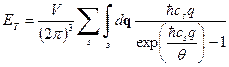 . (29)
. (29)
При вычислении интеграла важно удачно выбрать систему координат. Зачастую гораздо удобнее вместо декартовых координат использовать криволинейные.
То, какую систему координат удобно использовать при вычислении интеграла, определяется симметрией подынтегральной функции. В нашем интеграле подынтегральная функция не зависит от 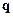 . Поэтому наш интеграл удобнее вычислять в сферических координатах. Поскольку подынтегральная функция не зависит от направления
. Поэтому наш интеграл удобнее вычислять в сферических координатах. Поскольку подынтегральная функция не зависит от направления 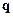 , то интегрирование по углам сферической системы координат даст полный телесный угол
, то интегрирование по углам сферической системы координат даст полный телесный угол 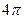 . Таким образом, наш трехмерный интеграл сводится к одномерному
. Таким образом, наш трехмерный интеграл сводится к одномерному
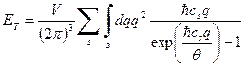 . (30)
. (30)
В этом интеграле имеет смысл перейти к новой безразмерной переменной 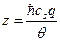 . Легко видеть, что после такой замены переменной все физические величины выйдут из под знака интеграла, и он станет безразмерной константой. Сделав эту замену переменной, получае
. Легко видеть, что после такой замены переменной все физические величины выйдут из под знака интеграла, и он станет безразмерной константой. Сделав эту замену переменной, получае
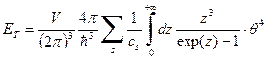 . (31)
. (31)
Таким образом, мы видим, что при низких температурах тепловой вклад во внутреннюю энергию кристаллической решетки пропорционален четвертой степени температуры. Следовательно, теплоемкость кристаллической решетки
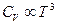 . (32)
. (32)
Теперь рассмотрим случай высоких температур, существенно превышающих произведение постоянной Планка на предельную частоту в спектре собственных колебаний
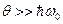 . (33)
. (33)
Поскольку частота любого собственного колебания 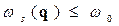 , то для всех собственных колебаний
, то для всех собственных колебаний 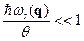 . Таким образом, в нашей задаче есть малый параметр. Проведя разложение по этому малому параметру, получаем
. Таким образом, в нашей задаче есть малый параметр. Проведя разложение по этому малому параметру, получаем
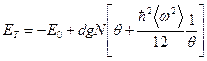 , (34)
, (34)
где
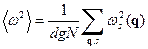 (35)
(35)
-среднее значение квадрата частоты
Соответственно, для теплоемкости имеем
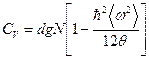 . (36)
. (36)
Таким образом, мы видим, что при высоких температурах теплоемкость кристаллической решетки выходить на константу 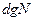 . Т.е. при высоких температурах теплоемкость кристаллической решетки выходит на классический закон Дюлонга-Пти.
. Т.е. при высоких температурах теплоемкость кристаллической решетки выходит на классический закон Дюлонга-Пти.
