Газ гармонических осцилляторов

Идеальный газ состоит из двухатомных молекул, являющихся линейными гармоническими осцилляторами, колеблющимися с частотой w. Найдем статистическую сумму и среднюю энергию одной частицы при температуре T , и теплоемкость колебательного движения.

Для линейного гармонического осциллятора используем

, ,

Подстановка в статистическую сумму частицы (3.15)

дает

,

где относительная температура

;

эффективная температура колебаний

.

Чем меньше масса атомов, тем выше частота их колебаний и больше эффективная температура

, , .

По формуле геометрической прогрессии

, ,

,

получаем

, (П.9.1)

Вероятность состояния n находим из (3.14)

.

Используем (П.9.1) и

,

,

получаем

.

Вероятность состояния экспоненциально убывает с увеличением номера состояния n.

Средняя энергия осциллятора следует из (3.17б)

.

Используем

, ,

,

С учетом

,

,

,

получаем

. (П.9.2)

Средний номер активизированного состояния при температуре T. Усредняем

,

находим

,

,

Подставляем (П.9.2)

,

получаем средний номер активизированного состояния

. (П.9.2а)

Уровни эквидистантные с шагом , уровню n соответствует n квантов энергии , поэтому есть среднее число квантов энергии в одном состоянии при температуре Т.

При низкой температуре , где , получаем

,

при высокой температуре

.

Колебательная теплоемкость молекулы

.

Используем (П.9.2)

,

получаем

. (П.9.2б)

При высокой температуре , где , в (П.9.2)

экспоненту разлагаем в ряд и оставляем первые три слагаемые

,

тогда

.

При высокой температуре колебательная теплоемкость частицы

не зависит от температуры и квантовая статистика переходит в классическую, что подтверждает условие (3.2) применимости классического описания.

При низкой температуре , в (П.9.2б)

пренебрегаем единицей в знаменателе и получаем

.

При находим , и выполняется третье начало термодинамики – теплоемкость обращается в нуль при . Это противоречит теореме классической физики о равном распределении энергии по степеням свободы.

ГАЗ ЧАСТИЦ С МАГНИТНЫМИ МОМЕНТАМИ

В МАГНИТНОМ ПОЛЕ

Идеальный газ N электронов со спином 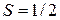и магнитным моментом находится в объеме V при температуре T в магнитном поле В. Проекции спина S и магнитного момента

на направление поля квантуются. Энергия магнитного момента в магнитном поле

получает значения

, .

Учтем распределение частиц по уровням энергии.

Статистическую сумму для магнитных состояний частицы находим из (3.15)

.

Вырождение отсутствует , тогда

, (П.9.11)

где относительная магнитная энергия

.

Вероятности состояний (3.14а)

равны

, .

Средняя энергия электрона

. (П.9.12)

Намагниченность системы. Средняя проекция магнитного момента электрона

. (П.9.13)

В сильном поле , , ,

,

возникает насыщение – все магнитные моменты выстраиваются по полю.

В слабом поле , ,

.

Магнитный момент системы N частиц

.

Система частиц со спином 1/2 проявляет парамагнитные свойства – установил В. Паули в 1926 г. Полученные результаты

,

являются следствием – вероятность основного состояния больше вероятности возбужденного состояния.

В классическом пределе при получаем , что соответствует теореме Бора–Ван-Левен – классическая система не проявляет магнитных свойств.

Магнитный момент единицы объема, т. е. намагниченность системы во внешнем поле согласно (П.9.13) равна

, (П.9.13а)

где – концентрация электронов.

Магнитная восприимчивость

.

С учетом

,

получаем

.

Магнитная восприимчивость увеличивается при понижении температуры и при увеличении концентрации частиц.

Классическому пределу соответствует

,

что согласуется с теоремой Бора–Ван-Левен.

Магнитное охлаждение. Если поле изменяется адиабатически, то есть настолько быстро, что теплообмена с окружающей средой не происходит, то сохраняются заселенность уровней и средняя проекция магнитного момента (П.9.13)

.

Следовательно, изменяется температура магнетика

. (П.9.13б)

Адиабатическое уменьшение магнитного поля охлаждает систему. Это объясняется тем, что снижение магнитного поля увеличивает среднюю магнитную энергию частицы (П.9.12)

.

Поскольку теплообмена с окружением не происходит, то это оттягивает часть тепловой энергии системы к магнитным моментам, в результате тепловое движение ослабевает.

Метод магнитного охлаждения на основе парамагнитных солей (сульфат гадолиния, хромокалиевые квасцы) предложили Петер Дебай и Уильям Джиок в 1926 г. Метод применяется для получения температур от 0,3 К до 5×10^–3 К. При меньшей температуре становится существенным взаимодействие между магнитными моментами, выстраивающее их параллельно друг другу, и они становятся зависимыми.

Самопроизвольная намагниченность. У намагниченной системы магнитные моменты выстроены параллельно и создают магнитное поле

.

Система может увеличивать это поле самопроизвольно. Борис Львович Розинг в 1892 г. и Пьер Вейсс в 1907 г. предложили в выражении для магнитного момента единицы объема (П.9.13а)

добавить собственное поле к внешнему намагничивающему полю , тогда намагниченность системы

.

При отсутствии внешнего поля получаем для M нелинейное уравнение

.

Замена дает

, (П.9.14)

где

(П.9.15)

– критическая температура Кюри.

При функция растет медленнее x, поэтому при температуре выше критической равенство (П.9.14) не выполняется. Остается лишь решение . Следовательно, при достаточно высокой температуре спонтанная намагниченность отсутствует.

При температуре ниже критической уравнение (П.9.14) имеет не равные нулю решения и система самопроизвольно намагничивается. Происходит фазовый переход второго рода – изменяется внутренняя симметрия системы, появляется ферромагнитное состояние в виде спонтанно намагниченных областей – доменов или полей Вейсса. При малых x используем и (П.9.14) получает вид

,

откуда

.

С учетом

находим спонтанную намагниченность

. (П.9.16)

Она достигает максимума при

.

Сравнение (П.9.15) и (П.9.16) с экспериментом, дает . Магнитное поле не может создать столь сильного взаимодействия магнитных моментов. Яков Ильич Френкель и независимо Вернер Гейзенберг показали в 1928 г., что электростатическое взаимодействие между электронами атомов сопровождается квантовым обменным взаимодействием, существенно превышающим магнитное взаимодействие, и этим объясняется спонтанная намагниченность ферромагнетика.