Решение уравнения Шредингера, т.е. математическое описание орбитали, возможно лишь при определенных, дискретных значениях характеристик, получивших название квантовых чисел.

Главное квантовое число n определяет основной запас энергии электрона, т.е. степень его удаления от ядра, или размер электронного облака (орбитали). Оно может принимать целочисленные значения от 1 до ∞.

Состояние электрона, характеризующееся определенным значением n,называется энергетическим уровнем электрона в атоме. Электроны, имеющие одинаковые значения n, образуют электронные слои (электронные оболочки), обозначаемые цифрами 1,2,3,4,5… или соответственно буквами: K, L, M, N, O…

Наименьшее значение энергии Е соответствует n=1. Остальным квантовым состояниям отвечают более высокие значения энергий, и электроны, находящиеся на этих энергетических уровнях, менее прочно связаны с ядром.

Орбитальное (побочное или азимутальное) квантовое числоlопределяет орбитальный момент количества движения электрона l = 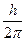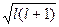и характеризует форму электронного облака (рис.34.2). Оно принимает все целочисленные значения от 0 до (n-1). Каждому n соответствует определенное число значений орбитального квантового числа, т.е. энергетический уровень представляет собой совокупность энергетических подуровней, несколько различающихся по энергиям. Число подуровней, на которые расщепляется уровень, равно номеру уровня (т.е. численному значению n). Эти подуровни имеют следующие буквенные обозначения:

Орбитальное квантовое число: 0 1 2 3 4

Подуровень s p d f g

Формы орбиталей, соответствующие различным значениям l

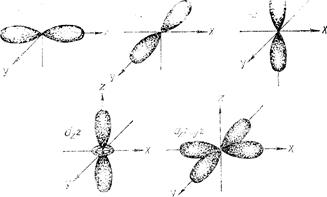
Рис.34.2

Таким образом, энергетический подуровень- это состояние электрона в атоме, характеризующееся определенным набором квантовых чисел n, l.Такое состояние электрона, соответствующее определенным значениям n и l (т.е. тип орбитали), записывается в виде сочетания цифрового обозначения n и буквенного l, например:4р (n=4; l=1);5d (n =5; l =2).

Магнитное квантовое число m_l определяет значение орбитального момента количества движения электрона L на произвольно выделенную ось z: L_z = 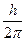m_l, т.е. характеризует пространственную ориентацию электронного облака. Оно принимает все целочисленные значения от – l до + l, например, при l=0 m_l =0, при l=1 m_l =-1,0,+1; при l=2 m_l =-2,-1,0,+1,+2

В общем виде любому значению при l соответствует (2l+1) значений магнитного квантового числа, т.е. (2l+1) возможных расположений электронного облака данного типа в пространстве. Следовательно, можно говорить, что число значений n указывает на число орбиталей с данным значением l. s –состоянию соответствует одна орбиталь, p- состоянию –три, d—состоянию – пять, f –состоянию семь. Все орбитали, соответствующие какому-либо состоянию, имеют одинаковую энергию и называются вырожденными.

Общее число орбиталей, из которых состоит любой энергетический уровень, равно n², а число орбиталей, составляющих подуровень - (2l+1).

Состояние электрона в атоме, характеризующееся определенными значениями квантовых чисел n, l, m_l,, т.е. определенными размерами, формой и ориентацией в пространстве электронного облака, называется атомной электронной оболочкой.

Спиновое квантовое число S характеризует собственный механический момент электрона, связанный с вращением его вокруг своей оси. Оно может иметь только два значения +1/2 или –1/2.

Общая характеристика состояния электрона в многоэлектронном атоме определяется принципом Паули: в атоме не может быть двух электронов, у которых все четыре квантовых числа были бы одинаковы.

Следовательно, на одной орбитали могут находится не более двух электронов, отличающихся друг от друга значениями спинового квантового числа; максимальная емкость энергетического подуровня 2(2l+1) электронов, а уровня 2n².

Спин электрона

Штерн и Герлах обнаружили, что узкий пучок атомов водорода, заведомо находящихся в s-состоянии, в неоднородном магнитном поле расщепляется на два пучка. В этом состоянии момент импульса электрона равен нулю. Магнитный момент атома, связанный с орбитальным движением электрона, пропорционален механическому моменту, поэтому он равен нулю и магнитное поле не должно оказывать влияния на движение атомов водорода в основном состоянии, т. е. расщепления быть не должно. Однако в дальнейшем при применении спектральных приборов с большой разрешающей способностью было доказано, что спектральные линии атома водорода обнаруживают тонкую структуру (являются дублетами) даже в отсутствие магнитного поля.

Для объяснения тонкой структуры спектральных линий, а также ряда других трудностей в атомной физике Д. Уленбек и С. Гаудомит предположили, что электрон обладает собственным неуничтожимым механическим моментом импульса, не связанным с движением электрона в пространстве, — спином.

Спин электрона (и всех других микрочастиц) — квантовая величина, у нее нет классического аналога; это внутреннее неотъемлемое свойство электрона, подобное его заряду и массе.

Если электрону приписывается собственный механический момент импульса (спин) L_s то ему соответствует собственный магнитный момент р_ms. Согласно общим выводам квантовой механики, спин квантуется по закону

L_s =ћ 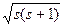, (34.15)

где s— спиновое квантовое число.

По аналогии с орбитальным моментом импульса, проекция L_sz спина квантуется так, что вектор L_s, может принимать 2s +1 ориентации. Так как в опытах Штерна и Герлаха наблюдались только две ориентации, то 2 s +1=2, откуда s = 1/2. Проекция спина на направление внешнего магнитного поля, являясь квантованной величиной, определяется выражением

L_sz= ћm_s (34.16)

где m_s — магнитное спиновое квантовое число; оно может иметь только два значения: m_s =±1/2.

Таким образом, опытные данные привели к необходимости характеризовать электроны (и микрочастицы вообще) добавочной внутренней степенью свободы. Поэтому для полного описания состояния электрона в атоме необходимо наряду с главным, орбитальным и магнитным квантовыми числами задавать еще магнитное спиновое квантовое число.