Энергетические характеристики термодинамических систем. первый закон термодинамики

Внутренняя энергия термодинамических систем.

Как известно, всякая термодинамическая система (ТС) состоит из большого числа микрочастиц, которые в процессе своего постоянного движения взаимодействуют друг с другом.

Полная энергия ТСЕ_полв общем случае состоит из внешней Е_вни полной внутренней U_полэнергий: Е_пол= Е_вн + U_пол.В свою очередь:

Е_пол = Е_вн + U_пол = Е_к + Е_п + U_к + U_п + U₀. (5.1.1)

Под внутренней энергией в термодинамике понимается только кинетическая энергия теплового движения молекул, атомов и ионов веществ, образующих ТС, и потенциальная энергия их взаимодействия:

U = U_к + U_п.(5.1.2)

Uесть функция состояния ТС, в самом общем случае определяемая как U = f(P,V,T). U является однозначной функцией состояния ТС.

Внутренняя энергия U, отнесённая к единице массы вещества ТС, u = U/М, где М – масса ТС, есть удельная внутренняя энергия, а к единице количества вещества, u_m = U/n_m= um- молярная внутренняя энергия. Соответственно [u] = Дж/кг, [u_m] = Дж/моль. В технических расчётах в термодинамике в основном используется u и u_m. В дальнейшем в основном будем рассматривать u.

Так как u есть функция состояния ТС, то Dи в ТПне зависит от характера процесса, а определяется лишь значениями u в начальном u₁ и конечном u₂ состояниях ТС:

Dи = u₂ – u₁, (5.1.4)

Независимость и от характера ТП математически выражается следующим образом:

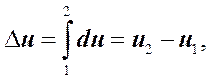(5.1.5)

Учитывая знак du, получаем, что в замкнутых ТП, то есть в циклах, изменение внутренней энергии ТСравно:

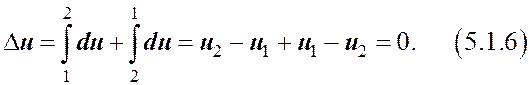
Работа деформирования термодинамических систем

Закрытые термодинамические системы

Работа в термодинамике определяется, так же, как и в механике, то есть умножением действующей на тело силы на путь её действия.

Совершаемая ТСработа при изменении V в общем случае зависит от параметров состояния Р, Т и v.

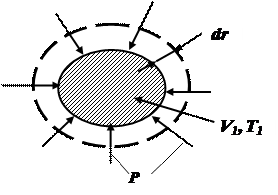
Рассмотрим закрытую равновесную ТС с начальным объёмом V₁, расположенную в ОС, которая оказывает на ТС абсолютное давление Р. Так как состояние рассматриваемой ТС равновесное, абсолютное давление во всех её точках будет одинаковым и равным абсолютному давлению на границе ТСс ОС, то есть равным Р. Закрытая ТС, как известно, не обменивается с ОС веществом, а обменивается только энергией.

Если температура ТС увеличится на dT, что практически не нарушает её равновесного состояния, то ТСувеличит свой начальный объём V₁ на dV, при этом каждая точка её поверхности переместится в ОС на расстояние dr. Учитывая, что сила давления F со стороны ОСна внешнюю поверхность ТС определяется как F = Р×S, где S – площадь внешней поверхности ТС, определим элементарную работу деформирования (конкретно расширения) dL_д, производимую ТСпри изменении своего объёма следующим образом:

dL_д = F×dr = РSdr. (5.2.1.1)

Но Sdr = dV, следовательно, имеем:

dL_д = РdV. (5.2.1.2)

Для 1 кг вещества ТС(5.2.1.2) приобретает вид:

dl_д = Рdv. (5.2.1.3)

Проинтегрировав (5.2.1.1) и (5.2.1.3) от начального состояния 1 ТСдо её конечного состояния 2, учтя при этом, что в общем случае Р может зависеть от V, получаем:

,

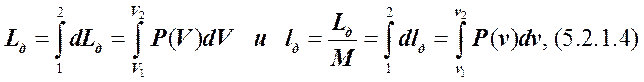где L_д, l_д – соответственно полная, Дж, и удельная, Дж/кг, работа деформирования (в рассмотренном случае расширения) ТС в ОС, при переходе ТС из начального состояния 1 в конечное состояние 2; V₂ – объём ТСв конечном состоянии 2, м³.

Если отнести работу деформирования газа к одному молю, то получим работу молярную работу деформирования l_𝛍, определяемую как:

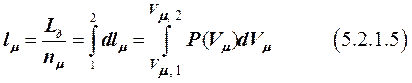
В связи с тем, что Р является функцией объёма ТС, то чтобы определить работу деформирования ТС необходимо знать вид функции Р(V) в течение всего ТП. Следовательно, работа деформирования зависит от характера ТП. Поэтому она является не функцией состояния ТС, как, например, U, а функцией ТП.Зависимость L_д, а, следовательно, и l_д, от пути интегрирования приводит к тому, что элементарная работа dL_д, а соответственно, и dl_д, с точки зрения высшей математикине являются полными дифференциалами.

Термин «работа расширения» отражают только частный случай деформирования ТС, и в самом общем случае более правильно называть L_д, а соответственно, и l_д, работой деформирования без указания, против каких сил она осуществляется.

В термодинамике для исследования равновесных (обратимых) ТП широко используют Рv-диаграмму, в которой осью абсцисс служит обычно v (в ряде случаев V), а осью ординат, соответственно, Р. Поскольку равновесное состояние ТСможет определяться всего лишь двумя основными термодинамическими параметрами, в том числе Ри v, то на Рv-диаграмме такое состояние изображается точкой. На рисунке точка 1 соответствует начальному равновесному состоянию ТС, а точка 2 – конечному. Последовательность равновесных состояний, представляющих собой равновесный ТП, изображается на Рv-диаграмме некоторой кривой, например 1-3-2 и 1-4-2.

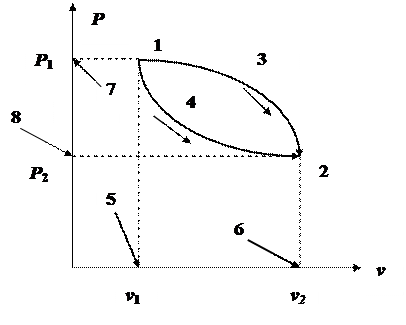Если ТС совершает круговой термодинамический процесс, то есть цикл, изображаемый на Рv-диаграмме, например некоторой замкнутой кривой 1-3-2-4-1, то при расширении ТС по кривой 1-3-2 она совершает положительную удельную работу деформирования, то есть удельную работу расширения, а по кривой 2-4-1– отрицательную удельную работу деформирования, то есть удельную работу сжатия. Таким образом, работа расширения ТС имеет знак плюс, а работа сжатия – знак минус.

Соответственно, разность S_1-3-2-6-5-1 - S_1-4-2-6-5-1 даёт удельную работу деформирования (в данном случае расширения) ТС в цикле. В связи с тем, что Рv-диаграмма наглядно показывает величину работы деформирования ТС, в ряде литературных источниках эта диаграмма получила название рабочей диаграммы.

Согласно геометрическому истолкованию определённого интеграла, величина l_д эквивалентна площади фигуры под кривой ТП. Следовательно, если ТП осуществляется по кривой 1-3-2, то работа деформирования ТC, а именно её расширения, l_д,1-3-2 будет равна площади S_1-3-2-6-5-1, то есть l_д,1-3-2 = S_1-3-2-6-5-1, а если по кривой 1-4-2, то имеем l_д,1-4-2 = S_1-4-2-6-5-1. Если термодинамические процессы будут идти в обратном направлении, то есть по кривым 2-3-1 и 2-4-1, то площади S_1-3-2-6-5-1 и S_1-4-2-6-5-1 будут численно оценивать уже работу сжатия.

Открытые термодинамические системы

Наиболее широкое применение нашли устройства, в которых осуществляется преобразование и передача энергии в потоке(поток – движущаяся масса чего-либо), когда газообразное рабочее тело перемещается из области с одними параметрами (Р₁ , v₁ , Т₁) в область с другими параметрами (Р₂ , v₂ , Т₂). Это имеет место в паровых и газовых турбинах, компрессорах, вентиляторах и тому подобное. При этом во всех этих технических устройствах в течение довольно больших периодов имеет место стационарное течение рабочих тел (стационарное течение потока – течение, при котором в любом сечении этого потока параметры среды остаются постоянными во времени).

Условие неразрывности течения в таких потоках заключается в постоянстве массового расхода М_t в любом сечении каналов, в которых эти потоки движутся:

М_t = Swr = Sw/v , (5.2.2.1)

где S – площадь поперечного сечения канала, м², [w] = м/с.

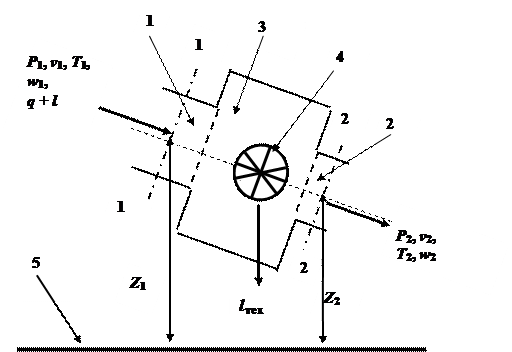
Рассмотрим схематически представленное на рисунке устройство, представляющее собой одно из возможных конструктивных исполнений открытой ТС. В данном устройстве по входному патрубку 1 рабочее тело с параметрами Р₁ , v₁ , Т₁подаётся в агрегат 3 со скоростью w₁. Здесь каждый килограмм рабочего тела в общем случае совершает техническую, то есть полезную, работу l_тех,например, приводя в движение ротор турбины 4, а затем выбрасывается в ОС через выходной патрубок 2 со скоростью w₂, имея параметры Р₂ , v₂ , Т₂.При этом, соответственно, Р₁ > Р₂ ,и в самом общем случае в агрегат 3 рабочим телом вносится определённое количество энергии в форме тепла q и механической работы l.

При отсутствии потерь рабочего тела через стенки корпуса рассматриваемого устройства объёмные расходы рабочего тела 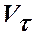через выходные сечения 1-1 и 2-2 патрубков 1 и 2 будут:

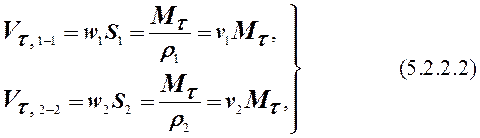
где r₁, r₂, v₁, v₂ - плотность, кг/м³, и удельный объём, м³/кг, рабочего тела в сечениях 1-1 и 2-2.

В рассматриваемом устройстве удельная работа деформирования (расширения) рабочего тела при переходе от сечения 1-1 к сечению 2-2 l_д,1-2 совершается рабочим телом на поверхностях, ограничивающих выделенный движущийся объём, то есть на стенках агрегата 3 и сечениях
1-1 и 2-2, выделяющих рассматриваемый объём рабочего тела в потоке. Таким образом, открытой ТС является часть потока рабочего тела, ограниченная реальными стенками агрегата 3 и сечениями 1-1 и 2-2, являющимися условными стенками. Часть стенок агрегата 3 выполняются обычно неподвижными, и работа расширения на них соответственно будет рана нулю. Другую часть стенок выполняют подвижными, например, поршень в цилиндре двигателя внутреннего сгорания, и на них рабочее тело будет совершать техническую (полезную) работу l_тех.

При входе в сечение 1-1 входного патрубка 1 рабочее тело вталкивается в агрегат 3. Для этого нужно преодолеть давление Р₁ , то есть выполнить определённую работу вталкивания l_вт. Для того чтобы войти в выходной патрубок 2 через сечение 2-2, рабочее тело должно вытолкнуть из этого патрубка такое же количество ранее находящегося в нём рабочего тела, преодолев давление Р₂. Таким образом, каждый килограмм рабочего тела, подойдя к сечению 2-2, производит определённую работу выталкивания l_выт, изменяя при этом свой удельный объём от v₁ до v₂.

Удельные работы вталкивания l_вт на входе в сечение 1-1 и выталкивания l_выт на выходе из сечения 2-2, учитывая (5.2.2.2), определим следующим образом:

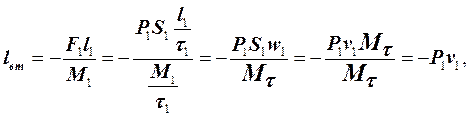(5.2.2.3)

аналогично получим:

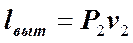, (5.2.2.4)

где F₁ – сила давления на входе в сечение 1-1, Н; l₁ – расстояние на которое за время t₁ переместится сечение потока, пересекающее сечение 1-1 в момент начала отсчёта этого времени, то есть при t = 0, с; М₁ – масса рабочего тела, прошедшая через сечение 1-1 за время t₁, кг.

Знак минус в правой части (5.2.2.3) указывает на то, что работу по вталкиванию рабочего тела в агрегат 3 осуществляет ОС, то есть поток рабочего тела, находящийся за границами рассматриваемой открытой ТС (до сечения 1-1). Соответственно работу по выталкиванию рабочего тела из агрегата 3 в ОС (за пределы сечения 2-2) осуществляет уже сама ТС, и поэтому в правой части (5.2.2.4) стоит знак плюс.

Алгебраическая сумма l_вт и l_выт даёт удельную работу проталкивания потока рабочего тела через агрегат 3 (в ряде литературных источниках её называют удельной работой вытеснения):

l_пр = l_вт + l_выт = Р₂ v₂ - Р₁ v₁ . (5.2.2.5)

Удельная работа проталкивания l_пр является только частью удельной работы деформирования l_д,1-2, совершаемой частью потока рабочего тела от сечения 1-1 до сечения 2-2, то есть открытой термодинамической системой. Часть l_д,1-2будет израсходована на изменение (в общем случае увеличение или уменьшение) кинетической энергии потока, которое в общем случае определяется как:

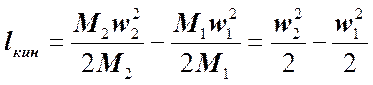. (5.2.2.6)

При отсутствии потерь рабочего тела через неплотности в корпусе агрегата 3 соответственно М₂ = М₁.

Если абсолютные отметки сечений 1-1 и 2-2 различаются, то часть l_д,1-2будет израсходована на изменение потенциальной энергии потока рабочего тела между этими сечениями, которое определяется следующим образом:

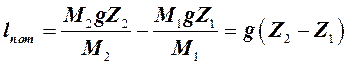(5.2.2.7)

где Z₁, Z₂ - абсолютные отметки сечений 1-1 и 2-2 относительно некоторой выбранной контрольной горизонтальной поверхности.

Кроме того, часть l_д,1-2 будет расходоваться на преодоление сил трения потока рабочего тела о стенки агрегата 3. Таким образом, имеем:

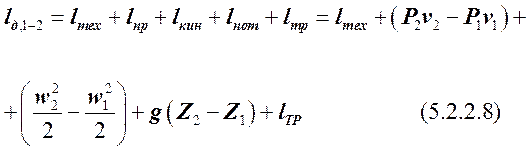
Данное уравнение есть уравнение энергии газового потока.

Учитывая, что согласно (5.2.1.3) dl_д = Рdv, а d(Рv) = Рdv + vdР, определим величину l_д,1-2следующим образом:

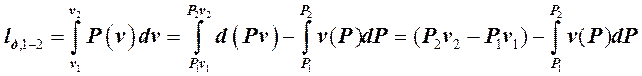
Заменив левую часть (5.2.2.8) на правую часть этого уравнения и выполнив соответствующие преобразования, получим:

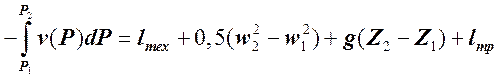(5.2.2.10)

Интеграл

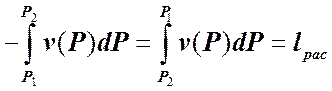(5.2.2.11)

получил название удельной располагаемой (потенциальной) работыпотока рабочего тела. Физический смысл этой работы применительно к потоку рабочего тела вытекает из правой части (5.2.2.10). Это та часть работы деформирования потока рабочего тела, которая остаётся в открытой ТС (в нашем рассматриваемом случае между сечениями 1-1 и 2-2) и превращается в другие виды работ, в том числе и в l_тех, то есть в полезную работу.

В устройствах для получения полезной работы обычно g(Z₂ - Z₁) » 0. Для этого случая из (5.2.2.10) получаем:

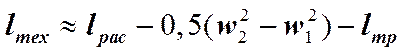(5.2.2.12)

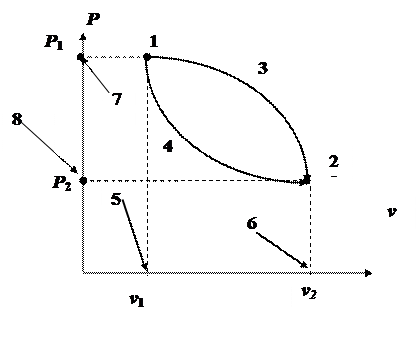На Рv-диаграммеl_рас отображается площадями S_1-3-2-8-7-1 и S_1-4-2-8-7-1. Если ТС совершает круговой ТП, то есть цикл, изображаемой на этой
Рv-диаграмме замкнутой кривой 1-3-2-4-1, то при расширении ТС по кривой 1-3-2 она совершает положительную удельную располагаемую работу, l_рас = S_1-3-2-8-7-1, а по кривой 2-4-1 – отрицательную удельную располагаемую работу, l_рас = S_1-4-2-8-7-1. Соответственно, разность S_1-3-2-8-7-1 -
- S_1-4-2-8-7-1 даёт удельную располагаемую работу ТС в цикле.

Следует отметить, что l_расиl_тех нельзя смешивать с работой деформирования l_д закрытых ТС. Различие между этой работой и l_рассl_тех заключается в том, что в потоках рабочих тел затрачивается энергия не только на деформирование рабочих тел (сжатие или расширение), но и на ввод их в ТС, вывод из ТС , а также и на изменение потенциальной и кинетической энергий этих потоков. Однако ТСсовсем не обязательно должна представлять собой поток рабочего тела. Она может быть и закрытой и при расширении внедрять часть своего вещества в ОС. Тогда часть энергии деформирования ТСв общем случае также будет затрачиваться на производство l_вт своего вещества в ОС, на изменениекинетической энергии вещества ТС в ходе вталкивания его в ОС l_кин , на преодоление сил трения l_тр и производство l_{пот .}

Следует отметить, что в ряде литературных источниках l_рас называют технической (полезной) работой. Вызвано это тем, что в них рассматриваются только обратимые ТП, в которых принимают l_пот = l_кин= l_тр = 0. В этом случае:

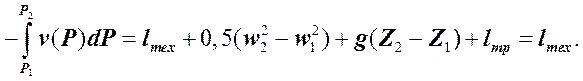
Как следует из (5.2.2.10), l_рас можно вычислить только в том случае, если известен вид зависимости v = f(P) в рассматриваемом ТП.

Если принять, что v, а следовательно и r, рабочего тела в рассматриваемом ТП не зависят от Р и Т (потоки капельной жидкости или газов с малыми скоростями), то получим:

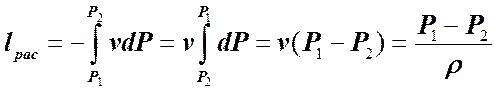.(5.2.2.13)

Заменив левую часть (5.2.2.10) правой частью (5.2.2.13), получаем:

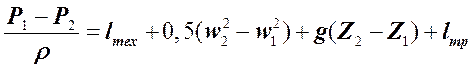, (5.2.2.14)

или:

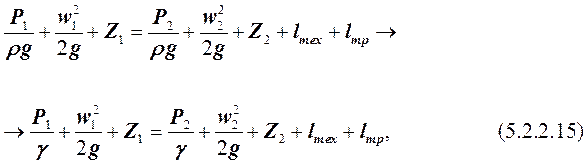
где g = rg – удельный вес рабочего тела, Н/м³.

Уравнение (5.2.2.15) было впервые получено в 1738 г. Д. Бернулли применительно к движению несжимаемой жидкости и получило название обобщённого уравнения Бернулли. Как видно, оно является частным случаем общего уравнения (5.2.2.10).

В дифференциальной форме уравнение (5.2.2.8)для расчёта удельной работы деформирования потока рабочего тела между сечениями 1-1 и 2-2 записывается в виде:

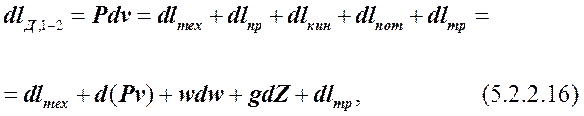
где 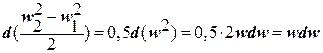; d(Pv) = P₂v₂ – P₁v₁ при P₂v₂ – P₁v₁ ® 0.

Учитывая, что 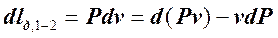, преобразуем (5.2.2.16) к виду:

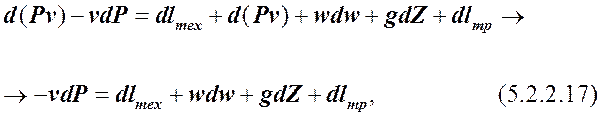
но 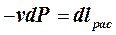, поэтому уравнение (5.2.2.17) для расчётов удельной располагаемой работы потока рабочего тела между сечениями 1-1 и 2-2 можно записать в виде:

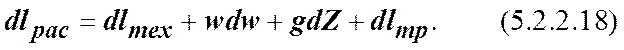
Следует отметить, что учёт в исходном уравнении (5.2.2.8) потерь энергии потоком рабочего тела на преодоление сил трения делает его справедливым как для равновесных, так и неравновесных ТП.