Полупроводника термическим методом

Лабораторная работа № 57

ОПРЕДЕЛЕНИЕ ШИРИНЫ ЗАПРЕЩЁННОЙ ЗОНЫ

ПОЛУПРОВОДНИКА ТЕРМИЧЕСКИМ МЕТОДОМ

Цель работы:

1. Исследовать зависимость удельной проводимости полупроводника от температуры.

2. Определить ширину запрещенной зоны полупроводника по зависимости удельной проводимости от температуры.

Теоретическое введение

Полупроводники относятся к классу веществ, удельная электропроводность (проводимость) σ которых меньше, чем у металлов и больше, чем у диэлектриков, и существенно зависит от воздействия вешних факторов (температуры, электрического поля, света и т. д.). Методы молекулярно-кинетической теории газов позволяют выразить σ через концентрацию n свободных носителей заряда, их заряд q и подвижность µ:

σ = qnµ, [Ом∙м]^-1. (1)

Подвижность µ носителей заряда представляет собой среднюю скорость направленного движения носителей (V_ср) в поле единичной напряженности Е:

µ = V_ср/Е, [м²/B∙с]. (2)

В металлах концентрация носителей заряда практически не зависит от температуры, так как все валентные электроны оторваны от своих атомов, поэтому температурная зависимость проводимости металлов целиком определяется температурной зависимостью подвижности носителей. Увеличение температуры приводит к возрастанию тепловых колебаний кристаллической решетки, на которых рассеиваются электроны (на квантовом языке говорят о столкновении электронов с фононами); при этом подвижность µ носителей и соответственно проводимость σ металла уменьшаются.

В полупроводниках проводимость σ с повышением температуры резко возрастает за счет увеличения числа носителей заряда, способных перемещаться под действием электрического поля

n = n₀exp(-ΔE/2kT), [м^-3] (3)

где n₀- концентрация свободных носителей заряда в состоянии термодинамического равновесия при очень высоких температурах (T → ∞), м^-3,

T - абсолютная температура полупроводника, К,

k - постоянная Больцмана; k = 1,38∙10^-23 Дж/К,

ΔE - ширина запрещенной зоны полупроводника (энергия активации), Дж.

Зависимость подвижности µ носителей заряда от температуры выражена гораздо слабее, чем их концентрация n, поэтому удельная электропроводность полупроводника имеет зависимость, аналогичную (3):

σ = σ₀exp(- ΔE/2kT), (4)

где σ₀ - удельная электропроводность полупроводника при T → ∞.

Зависимость σ от Т удобно представлять в полулогарифмических координатах. Логарифмируя (4), получим:

ln σ = ln σ₀ - ΔE/2kT. (5)

Температурная зависимость проводимости примесных полупроводников в осях ln σ = f(1/T) представлена на рисунке 1. Тангенс угла a_соб наклона этой прямой к оси абсцисс на участке собственной проводимости (III), обусловленном тепловым перебросом носителей з валентной зоны в зону проводимости, равен ΔE/2kT, то есть определяется шириной запрещённой зоны полупроводника.

Рисунок 1 - Температурная зависимость удельной проводимости примесных полупроводников в областях:

I - примесной проводимости;

II - истощения примеси;

III - собственной проводимости;

Углы наклона определяют:

a_пр - энергию активации примеси;

a_соб - ширину запрещенной зоны.

Для беспримесных (собственных) полупроводников концентрация носителей заряда и проводимость при данной температуре определяются шириной их запрещенной зоны (таблица 1).

Таблица 1 - Ширина запрещенной зоны ΔЕ и удельная проводимость σ элементов IV группы таблицы Менделеева при 300 К

Элемент	Алмаз	Кремний	Германий	Олово (серое)
ΔΕ, эВ	5,20	1,21	0,72	0,08
σ, [Ом∙м]-1	1∙10-10	3∙10-2	2∙100	5∙103

Для примесных полупроводников существенное влияние на проводимость оказывает концентрация введенной примеси N_пр. Так как энергия активации донорных и акцепторных примесей существенно меньше ширины запрещенной зоны ΔЕ, угол наклона зависимости ln σ = f(1/T) в области примесной проводимости α_пр будет существенно меньше, чем в области собственной проводимости a_соб (рисунок 1, области I и III соответственно).Если все примесные центры ионизованы, а собственная проводимость еще не наблюдается, то концентрация носителей заряда при увеличении температуры остается постоянной (область истощения примеси). Проводимость на этом участке падает за счет уменьшения подвижности носителей заряда (рисунок 1, область II). При высоких концентрациях примеси участок истощения может отсутствовать.

Таким образом, измеряя температурный ход зависимости удельной проводимости полупроводника, можно определить энергию активации примеси и ширину запрещенной зоны ΔЕ.

Описание установки

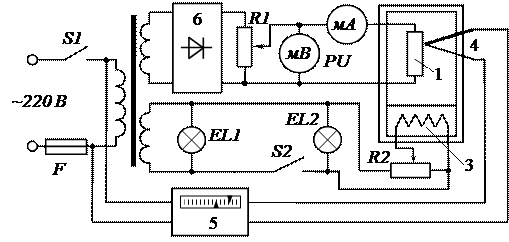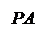
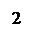Измерительная установка (рисунок 2) содержит образец полупроводника 1, помещенный в термостат 2. Нагрев термостата осуществляется путем подачи напряжения на нагревательный элемент 3; величина напряжения регулируется потенциометром R2. Температура образца контролируется с помощью хромель-копелевой термопары 4 и показывающего прибора 5. На образец полупроводника от выпрямителя 6 подается постоянное напряжение, величина которого регулируется потенциометром R1. Напряжение на образце и сила тока через него измеряются вольтметром PU и амперметром PA соответственно. Ключ S1 служит для включения стенда, ключ S2 – для подачи напряжения на печь 3. Индикатор EL1 сигнализирует, что стенд включён в сеть; индикатор EL2 указывает, что включена печь 3.

Рисунок 2 - Схема установки для исследования температурной зависимости удельной проводимости полупроводников.