Нанообъекты и волны де Бройля

ФИЗИЧЕСКИЕ ОСНОВЫ НАНОЭЛЕКТРОНИКИ

Корпускулярно-волновой дуализм и принцип Гейзенберга.

В классической физике мы обычно сталкиваемся с двумя типами объектов, а именно с частицами (типа точечных малых масс, которые фигурируют в уравнениях Ньютона) и волнами (типа электромагнитных или световых, поведение которых описывается уравнениями Максвелла). Однако при описании очень малых объектов, типа атома, оба варианта оказываются несостоятельными и мы вынуждены пользоваться понятиями квантовой механики, в основе которой лежит представление о дуальности «волна-частица», или, как говорят, о корпускулярно-волновом дуализме.

Еще в 1901 г. Планк предположил (для объяснения кривой излучения черного тела), что свет может излучаться или поглощаться лишь в виде некоторых порций- квантов или фотонов. При этом нергия фотона равна:

,

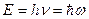где h- постоянная Планка (h=6.62∙10^-34Дж∙с, ħ=h/2 );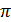

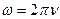- угловая частота.

Традиционно электроны рассматривались в качестве частиц, но в 1927 г. Девидсон и Джермер обнаружили явление дифракции электронов при отражении от поверхности кристалла никеля, как если бы они были волнами и подчинялись законам дифракции Брегга. Поэтому можно утверждать, что концепция дуализма основана на экспериментальных результатах. Действительно, как и показал де Бройль в 1924г., каждой частице с импульсом p можно сопоставить волну с длиной

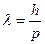
Это уравнение может быть переписано в виде:

,

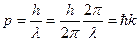где k- волновое число.

Другой чрезвычайно важный квантово-механический закон был открыт в 1927г., когда Гейзенберг сформулировал свой принцип неопределенности, в соответствии с которым в любом эксперименте произведение ошибок измерения импульса частицы 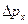и ее координаты 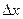всегда должно превышать 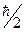, т.е.

.

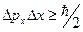При этом подчеркнем, что принцип неопределенности – фундаментальное свойство природы, а вовсе не связано с конкретным типом приборов, используемых в эксперименте. В другой более вам известной формулировке этот принцип устанавливает связь между ошибками измерений энергии частицы ΔЕ и временным промежутком Δt, требуемым для ее измерения

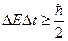
Итак, по де Бройлю любую микрочастицу можно отождествить с некоторой электромагнитной волной. При этом:

· ,

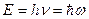где Е – энергия частицы,

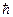- постоянная Планка,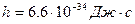

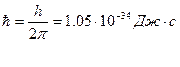
· Волновой вектор определяется импульсом

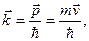
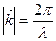
· Длина волны де Бройля

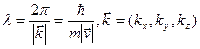
Т.о. де Бройль отождествил движущуюся материальную частицу с плоской электромагнитной волной следующего вида:

,

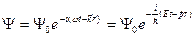где 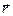- радиус-вектор

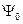- амплитуда плоской волны.

Нанообъекты и волны де Бройля

При определенных размерах частицы переходят к волновым свойствам. Наша задача определить эти размеры.

На основании формулы

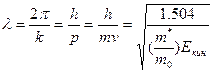
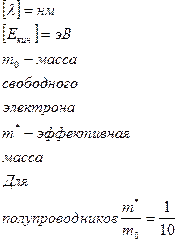
Кинетическая энергия при 300К:

Е_кин=kT=0.0259 эВ, тогда λ=25 нм=250 Å.

Для металлов Е_кин=Е_F=(1-10) эВ

При одних и тех же условиях длина волны де Бройля для электрона в металле на порядок и более меньше, чем в полупроводниках.

Т.о. если толщина тонких пленок или структур, из которых состоят нанообъекты соизмеримы с длиной волны де Бройля, то в таких объектах, называемых нанообъектами, можно ожидать проявления волновых свойств электрона. Отсюда ясно, что объекты наноэлектроники легче реализовать на п/п материалах, а не на металлах.