Оль свободной поверхностной энергии в термодинамических процессах. Поверхностное натяжение металлургических расплавов. Межфазное натяжение.
екция №16
ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ В СТАЛЕПЛАВИЛЬНЫХ ПРОЦЕССАХ.
оль свободной поверхностной энергии в термодинамических процессах. Поверхностное натяжение металлургических расплавов. Межфазное натяжение.
Роль свободной поверхностной энергии в термодинамических процессах
Металлургическая система металл – шлак – газ всегда является многокомпонентной и гетерогенной. В ней одновременно протекает множество процессов, степень взаимной связи которых весьма различна и определяется как свойствами компонентов системы и соотношением сил взаимодействия между ними, так и рядом внешних факторов, например, тепловым режимом, состоянием поверхности контакта фаз, интенсивностью перемешивания металла и т.д. Термодинамический анализ гетерогенных систем и изучение кинетики протекающих в них процессов требует учета свойств границ раздела фаз и происходящих на их поверхности явлений.
Поверхностные явления в металлургических процессах играют важную роль и должны учитываться при управлении ими. С поверхностными явлениями связано образование новых фаз, газовых пузырей в процессах окисления углерода, рафинирование металла, его кристаллизация из жидкой фазы и т.д.
В общем случае в объеме конденсированных систем (жидких и твердых) каждая частица (молекула, атом) окружена другими такими же частицами и испытывает притяжение к ним в сфере действия молекулярных сил радиусом 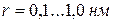 , равнодействующая которых равна нулю. У поверхности вещества (на границе с газом или вакуумом) частицы, расположенные на расстоянии меньше
, равнодействующая которых равна нулю. У поверхности вещества (на границе с газом или вакуумом) частицы, расположенные на расстоянии меньше 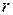 , находятся в ином состоянии: силы их притяжения, направленные внутрь объема нормально к поверхности вещества, не уравновешены, так как со стороны газа (вакуума) притяжение весьма слабое или отсутствует. Такие частицы образуют некоторый слой, в котором осуществляется переход от потенциального поля одной фазы к потенциальному полю другой. Толщина слоя составляет от нескольких единиц до десятков атомных слоев, однако, указать его точные границы невозможно, поэтому переходный слой рассматривают как поверхность раздела, выбранный внутри или вблизи переходного слоя. С этой поверхностью раздела, называемой по имени исследователя поверхностных явлений в условиях равновесия фаз гетерогенных систем «гиббсовской поверхностью раздела» или «поверхностью натяжения» связывают все термодинамические свойства переходного слоя за исключением объема.
, находятся в ином состоянии: силы их притяжения, направленные внутрь объема нормально к поверхности вещества, не уравновешены, так как со стороны газа (вакуума) притяжение весьма слабое или отсутствует. Такие частицы образуют некоторый слой, в котором осуществляется переход от потенциального поля одной фазы к потенциальному полю другой. Толщина слоя составляет от нескольких единиц до десятков атомных слоев, однако, указать его точные границы невозможно, поэтому переходный слой рассматривают как поверхность раздела, выбранный внутри или вблизи переходного слоя. С этой поверхностью раздела, называемой по имени исследователя поверхностных явлений в условиях равновесия фаз гетерогенных систем «гиббсовской поверхностью раздела» или «поверхностью натяжения» связывают все термодинамические свойства переходного слоя за исключением объема.
Обозначив индексами 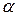 и
и 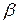 параметры, относящиеся соответственно к двум фазам
параметры, относящиеся соответственно к двум фазам 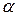 и
и 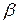 , а индексом «пов» – к переходному слою (поверхности натяжения), можно записать:
, а индексом «пов» – к переходному слою (поверхности натяжения), можно записать:
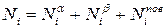 (4.1)
(4.1)
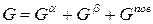 (4.2)
(4.2)
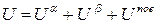 (4.3)
(4.3)
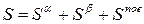 (4.4)
(4.4)
где 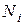 – число молекул
– число молекул 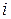 -того сорта в объеме системы;
-того сорта в объеме системы;
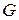 – свободная энергия;
– свободная энергия;
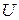 – внутренняя энергия;
– внутренняя энергия;
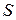 – энтропия системы.
– энтропия системы.
Из уравнений (4.1) – (4.4) вытекает термодинамическое определение свободной поверхностной энергии, называемой также энергией Гиббса поверхности:
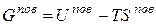 (4.5)
(4.5)
Эта часть полной свободной энергии системы эквивалентна работе, которая должна быть затрачена на перемещение частицы из глубинных слоев фазы 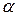 к поверхности ее раздела с фазой
к поверхности ее раздела с фазой 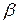 (газом, вакуумом).
(газом, вакуумом).
Удельная поверхностная энергия, т.е. количество свободной поверхностной энергии, приходящейся на единицу поверхности натяжения 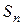 между рассматриваемым веществом и газом (вакуумом) определяется как поверхностное натяжение и обозначается
между рассматриваемым веществом и газом (вакуумом) определяется как поверхностное натяжение и обозначается 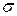 :
:
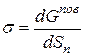 . (4.6)
. (4.6)
Так как поверхностное натяжение определяется энергией, приходящейся на единицу площади, единицей его измерения является 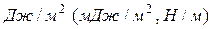 .
.
Роль поверхностных явлений в термодинамических системах наглядно отражает объединенное уравнение первого и второго начал термодинамики, выражающее приращение энергии Гиббса через алгебраическую сумму приращений других видов энергии:
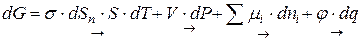 , (4.7)
, (4.7)
где 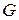 – энергия Гиббса;
– энергия Гиббса;
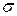 – поверхностное натяжение;
– поверхностное натяжение;
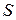 – энтропия;
– энтропия;
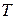 – температура;
– температура;
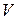 – объем;
– объем;
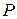 – давление;
– давление;
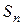 – площадь поверхности;
– площадь поверхности;
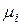 – химический потенциал компонента
– химический потенциал компонента 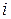 ;
;
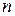 – число молей компонента
– число молей компонента 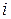 ;
;
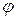 – электрический потенциал;
– электрический потенциал;
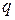 – количество электричества.
– количество электричества.
Стрелки указывают на возможные превращения поверхностной энергии в энергию Гиббса, в теплоту, в механическую, химическую и электрическую энергии, сопровождающиеся определенными поверхностными явлениями: изменением реакционной способности веществ с изменением дисперсности фаз, адгезией, смачиваемостью, капиллярностью, адсорбцией и электрическими явлениями.
Поскольку уравнение (4.7), кроме энергии Гиббса, может быть записано и относительно других термодинамических потенциалов, а именно внутренней энергии 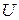 , энергии Гельмгольца
, энергии Гельмгольца 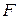 и энтальпии
и энтальпии 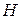 , то при соответствующих постоянных параметрах
, то при соответствующих постоянных параметрах 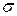 можно выразить тождеством:
можно выразить тождеством:
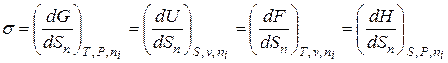 . (4.8)
. (4.8)
Отсюда следует, что поверхностное натяжение есть частная производная от любого термодинамического потенциала по площади межфазной поверхности при постоянных соответствующих параметрах. Однако чаще поверхностное натяжение выражают через производную от энергии Гиббса, поскольку условия равенства давления и температуры в системе легко осуществимы при исследовании, особенно в металлургических процессах.
Поверхностное натяжение металлургических расплавов
Численные значения поверхностного натяжения металлургических расплавов зависят от их состава и температуры.
По определениям различных исследователей, поверхностное натяжение чистого железа при температурах 1550...1650 °С колеблется от 1650 до 1950 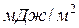 .
.
Влияние основных компонентов металлургических систем на изменение поверхностного натяжения связано с адсорбцией и будет подробнее рассмотрено ниже, при изложении материала об адсорбционных процессах.
Наиболее достоверные данные о поверхностном натяжении расплавов металлов и металлических сплавов на основе железа при температуре 1600 °С приведены в табл. 4.1.
Таблица 4.1 — Поверхностное натяжение расплавов металлов и
металлических сплавов на основе железа при
температуре 1600 °С
| Металл | Сплав | |||
| Обозгначения | 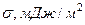 | Состав | Массовая доля компонента примеси, % | 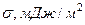 |
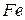 | 1730 – 1860 | 0,2 | ||
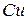 | 1260 – 1400 | 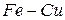 | 0,5 | |
| 3,0 | ||||
| 5,0 | ||||
| 10,0 | ||||
| 50,0 | ||||
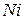 | 1770 – 1880 | 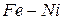 | 1,3 | |
| 2,0 | ||||
| 3,0 | ||||
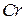 | 1500 – 1560 | 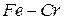 | 1,0 | |
| 1,2 | ||||
| 4,8 | ||||
| 9,7 | ||||
| 24,3 | ||||
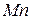 | 1090 – 1175 | 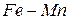 | 0,6 | |
| 1,3 | ||||
| 3,0 | ||||
| 6,2 | ||||
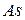 | — | 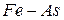 | 0,1 | |
| 0,2 | ||||
| 0,3 | ||||
| 0,8 |
При повышении температуры силы взаимного притяжения между молекулами ослабляются как внутри фаз, так и в поверхностном слое, поэтому в общем случае с повышением температуры поверхностное натяжение уменьшается, т.е. 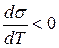 .
.
Впервые зависимость поверхностного натяжения от состава и температуры была дана Б. Шишковским в виде эмпирического уравнения, справедливость которого была подтверждена более поздними исследованиями:
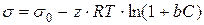 , (4.9)
, (4.9)
где 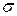 и
и 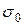 – поверхностные натяжения раствора и растворителя соответственно;
– поверхностные натяжения раствора и растворителя соответственно;
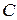 – концентрация раствора;
– концентрация раствора;
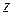 и
и 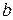 – константы;
– константы;
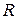 – универсальная газовая постоянная;
– универсальная газовая постоянная;
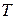 – абсолютная температура.
– абсолютная температура.
Поверхностное натяжение шлака 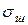 определяется силой связи между элементарными частицами, составляющими шлак. Оно в значительной мере зависит от состава шлака и колеблется в пределах 200...600
определяется силой связи между элементарными частицами, составляющими шлак. Оно в значительной мере зависит от состава шлака и колеблется в пределах 200...600 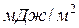 , что в 3 – 9 раз меньше величины
, что в 3 – 9 раз меньше величины 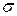 жидкого железа (1800
жидкого железа (1800 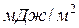 ). Для приближенной оценки межчастичного взаимодействия используют величину энергии взаимодействия
). Для приближенной оценки межчастичного взаимодействия используют величину энергии взаимодействия 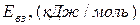 , отнесенную к произведению валентности на число атомов в химической формуле вещества. В свою очередь
, отнесенную к произведению валентности на число атомов в химической формуле вещества. В свою очередь 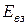 зависит от энергии ионизации, сродства кислорода к электрону, энергии диссоциации молекул кислорода, теплот плавления оксида и сублимации металла. По снижению энергии взаимодействия
зависит от энергии ионизации, сродства кислорода к электрону, энергии диссоциации молекул кислорода, теплот плавления оксида и сублимации металла. По снижению энергии взаимодействия 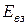 с анионами кислорода катионы основных оксидов, составляющих металлургические шлаки, располагаются в следующий ряд:
с анионами кислорода катионы основных оксидов, составляющих металлургические шлаки, располагаются в следующий ряд: 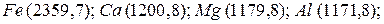
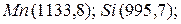
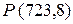 . Поверхностная активность и распределение оксидов в поверхностном слое и в объеме их расплавов приведены в табл. 4.2. Как видно,
. Поверхностная активность и распределение оксидов в поверхностном слое и в объеме их расплавов приведены в табл. 4.2. Как видно, 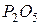 и
и 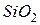 характеризуются меньшими значениями
характеризуются меньшими значениями 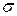 и повышенным содержанием в поверхностном слое. Они относятся к наиболее сильным поверхностно-активным веществам, снижающим
и повышенным содержанием в поверхностном слое. Они относятся к наиболее сильным поверхностно-активным веществам, снижающим 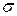 шлаков. Кроме
шлаков. Кроме 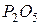 и
и 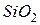 ,
, 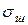 снижают
снижают 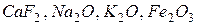 . Поверхностно-инактивными оксидами, увеличивающими
. Поверхностно-инактивными оксидами, увеличивающими 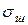 , являются
, являются 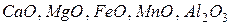 .
.
Таблица 4.2 — Характеристика оксидов, входящих в состав
металлургических шлаков
| Оксид | Поверхностное натяжение оксидов 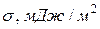 | Массовая доля в шлаке, % | 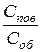 | |
поверхностная 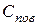 | объемная 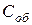 | |||
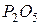 | 3,1 | 3,1 | ||
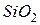 | 300 – 400 | 36,0 | 1,7 | |
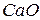 | 27,0 | 0,8 | ||
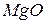 | 5,0 | 0,8 | ||
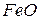 | 570 – 590 | 8,3 | 0,6 | |
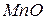 | 590 – 630 | 11,0 | 0,7 | |
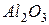 | 640 – 720 | 2,3 | 0,5 |
С повышением температуры с одной стороны увеличиваются кинетическая энергия частиц и расстояния между ними, что способствует уменьшению 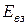 и снижению
и снижению 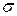 , с другой стороны – уменьшается адсорбция поверхностно-активных веществ и частичная замена в прилежащем к поверхности слое катионов
, с другой стороны – уменьшается адсорбция поверхностно-активных веществ и частичная замена в прилежащем к поверхности слое катионов 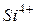 и
и 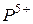 катионами
катионами 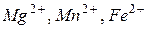 и
и 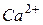 , прочнее связывающихся с ионами
, прочнее связывающихся с ионами 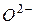 , что приводит к повышению прочности связи поверхностного слоя с объемом расплава и увеличению
, что приводит к повышению прочности связи поверхностного слоя с объемом расплава и увеличению 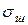 . Поэтому суммарное изменение
. Поэтому суммарное изменение 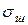 под влиянием температуры незначительно: повышение температуры на 100 °С снижает
под влиянием температуры незначительно: повышение температуры на 100 °С снижает 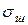 на величину, колеблющуюся в пределах от 25 для маложелезистых шлаков до 40
на величину, колеблющуюся в пределах от 25 для маложелезистых шлаков до 40 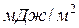 для шлаков с повышенным содержанием оксида железа.
для шлаков с повышенным содержанием оксида железа.
Некоторые авторы считают, что поверхностно-активные оксиды способствуют пенообразованию, адсорбируясь на границе раздела шлака с пузырьками 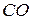 и образуя устойчивые пленки (наподобие мыльной пены). Однако степень вспенивания шлака зависит не только от его поверхностного натяжения, но и от вязкости шлака и механической прочности пленок на пузырьках.
и образуя устойчивые пленки (наподобие мыльной пены). Однако степень вспенивания шлака зависит не только от его поверхностного натяжения, но и от вязкости шлака и механической прочности пленок на пузырьках.
Межфазное натяжение
На границе раздела металл-шлак молекулы веществ испытывают различное воздействие со стороны граничащих фаз, определяющих межфазное натяжение между ними.
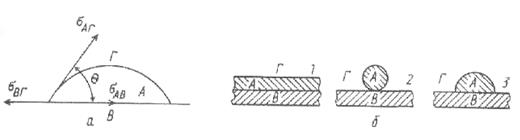
1 – полное смачивание ( 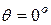 ); 2 – полное несмачивание (
); 2 – полное несмачивание ( 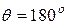 ); 3 – частичное смачивание (
); 3 – частичное смачивание ( 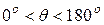 )
)
Рисунок 4.1 — Равновесие поверхностных натяжений при
образовании капли (а) и различные случаи
смачивания (б)
Величина межфазного натяжения зависит от поверхностных натяжений (энергии) контактирующих фаз. Ее определяют с учетом краевого угла смачивания 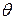 , характеризующего растекание шлака по металлу. Угол смачивания образуется между поверхностью металла и касательной к поверхности, находящейся на металле шлаковой капли
, характеризующего растекание шлака по металлу. Угол смачивания образуется между поверхностью металла и касательной к поверхности, находящейся на металле шлаковой капли 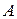 в точке ее соприкосновения с металлом
в точке ее соприкосновения с металлом 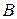 (рис. 4.1). При большей смачиваемости угол
(рис. 4.1). При большей смачиваемости угол 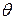 уменьшается и соответственно уменьшается межфазное натяжение
уменьшается и соответственно уменьшается межфазное натяжение 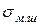 между металлом и шлаком, которое рассчитывают по формуле:
между металлом и шлаком, которое рассчитывают по формуле:
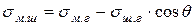 . (4.10)
. (4.10)
Из уравнения (4.10) и рис. 4.1 видно, что лишь при полном смачивании (когда 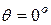 , а
, а 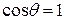 ) соблюдается правило Антонова: межфазное натяжение равно разности поверхностных натяжений соприкасающихся фаз.
) соблюдается правило Антонова: межфазное натяжение равно разности поверхностных натяжений соприкасающихся фаз.
С.И. Попель с сотрудниками вывели более точную формулу для расчета межфазного натяжения в случае, когда подкладкой для капли шлака является жидкий металл. В этой формуле учтено частичное погружение капли шлака в металл, например, в жидкое железо.
После ряда тригонометрических преобразований получено следующее выражение для расчета межфазного натяжения на поверхности раздела металл – шлак:
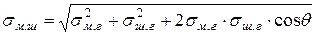 , (4.11)
, (4.11)
где 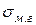 и
и 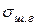 – поверхностное натяжение металла и шлака соответственно (на границе с газом или с вакуумом).
– поверхностное натяжение металла и шлака соответственно (на границе с газом или с вакуумом).
Уравнение (4.11) можно использовать для расчетов аХ2 на поверхности контакта двух любых жидкостей с различной плотностью (индекс 1 относится к более тяжелой жидкости, а индекс 2 – к более легкой).
Результаты расчетов по формуле (4.10) незначительно отличаются от полученных по уравнению (4.11). Так, при 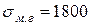 и
и 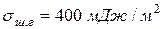 получаем следующие значения
получаем следующие значения 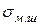 :
:
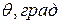 ………………….. ………………….. | |||||||
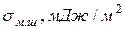 (4.10)…. (4.10)…. | |||||||
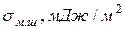 (4.11)…. (4.11)…. |
Таким образом, с достаточной для практических целей точностью можно рассчитывать межфазное натяжение на границе металл – шлак по простой формуле (4.10).
Поскольку на границе металл-шлак происходит контакт разноименно заряженных поверхностей, снижающий силу связи одноименно заряженных частиц, межфазное натяжение всегда меньше, чем поверхностное натяжение металла. Так, при 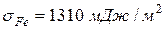 и
и 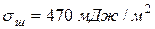 (
( 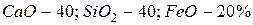 ) межфазное натяжение
) межфазное натяжение 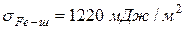
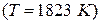 .
.
При малой растворимости одной фазы в другой, величина межфазного натяжения максимальна и близка к величине поверхностного натяжения фазы с более сильным межчастичным взаимодействием.
При введении в шлак компонентов, переходящих в металл, 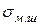 снижается. То же происходит и при наличии в металле компонентов, растворимых в шлаке.
снижается. То же происходит и при наличии в металле компонентов, растворимых в шлаке.
На межфазной границе поверхностно-активным компонентом, снижающим 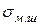 , может быть компонент, более активно взаимодействующий с частицами расплава, если его атомы с большей силой удерживаются поверхностью другого расплава.
, может быть компонент, более активно взаимодействующий с частицами расплава, если его атомы с большей силой удерживаются поверхностью другого расплава.
Межфазная энергия в равновесных системах зависит от природы и строения контактирующих фаз и уменьшается при сближении их свойств.
