Задача 5. Для системи, що складається з частинок одного сорту, довести співвідношення

.

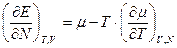Розв’язання. При незалежних змінних 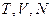згідно з (6.13) термодинамічним потенціалом є енергія Гельмгольца 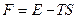. Рівняння Гіббса-Гельмгольца (5.31), яке випливає з цього співвідношення, з урахуванням залучення змінної 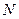можна переписати у вигляді

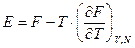. (1)

Диференціюючи (1) за 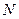при постійних 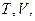знайдемо

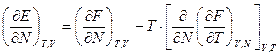
або, змінюючи порядок диференціювання в змішаній похідній,

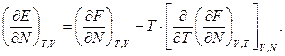(2)

Оскількі відповідно до (6.16): 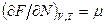, з (2) отримуємо

,

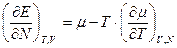що й потрібно було довести.

Задача 6. Хімічний потенціал однокомпонентного ідеального газу заданий у вигляді

,

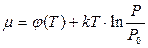де 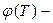деяка функція абсолютної температури, 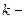стала Больцмана. Отримати вираз для великого термодинамічного потенціалу .

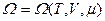Розв’язання. Відповідно до (6.17) і на підставі термічного рівняння стану ідеального газу можна записати

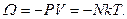(1)

Виражаючи з умови тиск 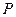і порівнюючи з (1), знайдемо

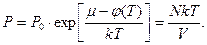(2)

Повертаючись до рівності (1), остаточно отримаємо

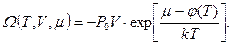
Задача 7. Показати, що хімічний потенціал є однорідною функцією нульового степеня величин .

Розв’язання. На підставі теореми Ейлера (1.14) для випадку 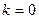в умовах задачі маємо:

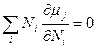. (1)

Ліву частину (1) згідно з (6.16) можна записати у вигляді

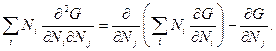(2)

З урахуванням результату задачі 4 цієї глави знаходимо

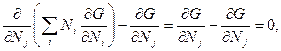(3)

що й потрібно було довести.

Задачі для самостійного розв’язування

6.1. Показати, що будь-який інтенсивний параметр є однорідною функцією нульового степеня екстенсивних змінних.

6.2. Довести, що для випадку, коли незалежними змінними системи є тиск 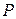, ентропія 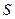і зовнішні параметри 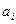крім об’єму 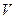, термодинамічним потенціалом буде ентальпія 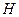, визначена для простої 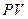-системи.

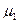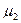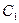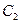6.3. Показати, що для системи, яка складається з двох однотипних компонентів, можлива логарифмічна залежність хімічних потенціалів і цих компонентів від складу (тобто від концентрацій і відповідно).

6.4. Для ідеального газу відомо, що 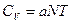( 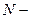число молекул, 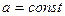). Знайти для нього хімічний потенціал .

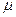6.5.Система складається з 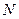частинок одного сорту. Довести співвідношення

.

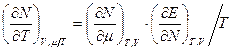6.6.Довести співвідношення для різниці теплоємностей

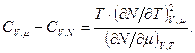
Розділ 7

ТРЕТЄ НАЧАЛО ТЕРМОДИНАМІКИ

Теоретичні відомості

Формулювання. Зараз відомо, що при наближенні абсолютної температури термодинамічної системи до нуля остання починає набувати особливих - квантових властивостей. Проявлення таких властивостей у багаточастинкових систем виявлено в першому десятиріччі 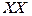-го століття в умовах експериментального досягнення достатньо низьких температур 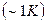. У результаті узагальнення багатьох дослідних даних В. Нернстом був сформульований фізичний закон - третє начало термодинаміки, відповідно до якого з наближенням температури до 0 К ентропія 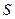будь-якої рівноважної системи в ізотермічних процесах перестає залежати від будь-яких термодинамічних параметрів стану, прагнучи до деякого постійного значення 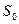. Пізніше М. Планк доповнив це твердження припущенням, що 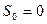. Отже, математично третє начало можна записати у вигляді

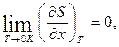(7.1)

де 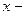будь-який термодинамічний параметр. Як бачимо, згідно з (7.1) при 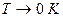зникає різниця між ізотермічним і адіабатним процесами. Звернемо також увагу на те, що при 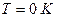на діаграмі 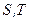вісь ентропії 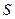повинна зливатися в точку, тому коректно її проводити на рівні деякої температури вище 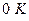. Зараз справедливість третього начала обгрунтована для усіх рівноважних систем. Підкреслимо також (квантова статистика це показує), що третє начало термодинаміки є макроскопічним проявленням квантових властивостей багаточастинкових систем при низьких температурах.

Наслідки. З третього начала безпосередньо випливає недосяжність температури 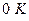. Дійсно, послідовне охолодження термодинамічної системи можна реалізувати чергуванням адіабатного і ізотермічного процесів. Спершу система здійснює роботу 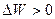, що в умовах 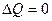призводить до зниження температури, потім відбувається ізотермічне відновлення значень зовнішніх параметрів, яке супроводжується зменшенням ентропії, і т.д. Однак при кожному наступному ізотермічному процесі зменшення ентропії відповідно до (7.1) буде слабшати, що не дозволить за скінченне число кроків досягти 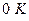. До цієї температури можна лише асимптотично наближатися.

Виявляється, що з недосяжності 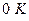в свою чергу можна вивести (7.1), тобто цей наслідок логічно еквівалентний третьому началу термодинаміки.

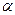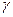Наступний важливий наслідок стосується поведінки термічних коефіцієнтів і при 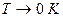. З визначень (0.20) і (0.22) маємо: 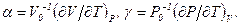Із співвідношень Максвелла (5.21) і (5.14) відповідно знаходимо, що при цьому 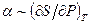і 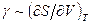. На основі (7.1) робимо остаточний висновок, що термічні коефіцієнти розширення 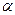і пружності 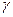наближаються до нуля при 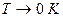. Цей же висновок очевидний і для термодинамічних коефіцієнтів 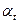і 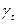. У загальному випадку для системи з зовнішнім параметром 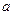на тій же підставі отримуємо

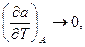
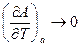(7.2)

при .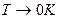

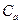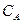Покажемо тепер, що з третього начала випливає наближення до нуля теплоємностей і при 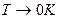. Узагальнюючи результати задачі 1 з розділу 3 на Aa-систему, з них можна записати формули для ентропії:

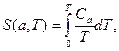
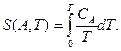(7.3)

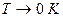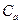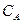Оскільки за третім началом ентропія при залишається скінченною величиною, інтеграли (7.3) в нижній межі повинні збігатися. Для цього і в свою чергу повинні мати асимптотику: 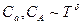, де 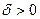. Звідси при 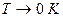з необхідністю маємо .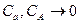