Циркуляция вектора магнитного поля в вакууме. Магнитные поля соленоида и тороида

Аналогично циркуляции вектора напряженности электростатического поля вводят циркуляцию вектора магнитной индукции. Циркуляцией вектора 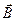по заданному замкнутому контуру называется интеграл

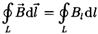
где 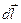— вектор элементарной длины контура, направленной вдоль обхода контура; 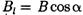— составляющая вектора 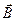в направлении касательной к контуру (с учетом выбранного направления обхода); α — угол между векторами 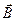и .

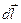Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора 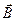): циркуляция вектора 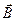по произвольному замкнутому контуру равна произведению магнитной постоянной μ₀ на алгебраическую сумму токов, охватываемых этим контуром:

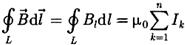(1)

где п — число проводников с токами, охватываемых контуром L произвольной формы.

Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого образует с направлением обхода по контуру правовинтовую систему; ток противоположного направления считается отрицательным.

Циркуляция вектора В длязамкнутого контура в виде окружности радиуса r равна

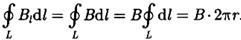
Согласно выражению (1), получим В∙2πr = μ₀I (ввакууме), откуда

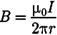
Итак, циркуляция вектора 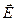электростатического поля всегда равна нулю, т. е. электростатическое поле является потенциальным. Циркуляция вектора 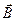магнитного поля не равна нулю. Такое поле называется вихревым.

Теорема о циркуляции вектора 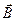имеет в учении о магнитном поле такое же значение, как теорема Гаусса в электростатике, так как позволяет находить магнитную индукцию поля без применения закона Био — Савара — Лапласа.

Рассчитаем, применяя теорему о циркуляции, индукцию магнитного поля внутри соленоида. Рассмотрим соленоид длиной l, имеющий N витков, по которому течет ток 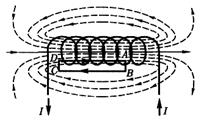(рис.).

Рис.

Длину соленоида считаем во много раз больше, чем диаметр его витков, т.е. рассматриваемый соленоид бесконечно длинный.

На рис. представлены линии магнитной индукции внутри и вне соленоида. Чем соленоид длиннее, тем меньше магнитная индукция вне его. Поэтому приближенно можно считать, что поле бесконечно длинного соленоида сосредоточено целиком внутри него, а полем вне соленоида можно пренебречь.

На участке вне соленоида В = 0.

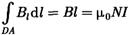(2)

Из (2) приходим к выражению для магнитной индукции поля внутри соленоида (в вакууме):

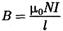(3)

Важное значение для практики имеет также магнитное поле тороида — кольцевой катушки, витки которой намотаны на сердечник, имеющий форму тора (рис.). Магнитное поле, как показывает опыт, сосредоточено внутри тороида, вне его поле отсутствует.

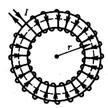Рис.

Линии магнитной индукции в данном случае, как следует из соображений симметрии, есть окружности, центры которых расположены по оси тороида. В качестве контура выберем одну такую окружность радиусом r. Тогда, по теореме о циркуляции (1), 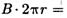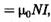откуда следует, что магнитная индукция внутри тороида (в вакууме)

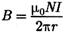
где N — число витков тороида.

Если контур проходит вне тороида, то токов он не охватывает и В∙2πr = 0. Это означает, что поле вне тороида отсутствует (что показывает и опыт).