Магнитное поле внутри соленоида

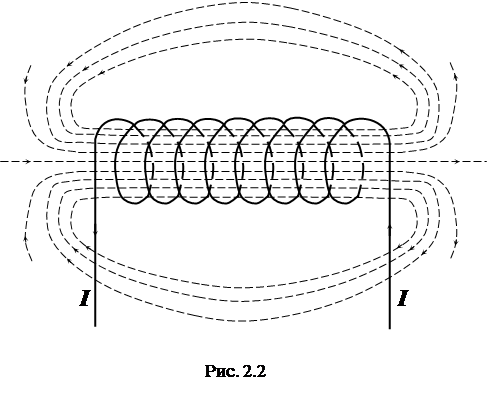Электрический ток, проходя через обмотку соленоида, создает во внутренней полости магнитное поле. Если длина соленоида во много раз превосходит его диаметр, то такой соленоид можно с хорошим приближением считать бесконечно длинным.

В этом случае магнитное поле снаружи пренебрежимо мало, а поле внутри соленоида практически однородно (неоднородность проявляется лишь около его концов рис. 2.2).

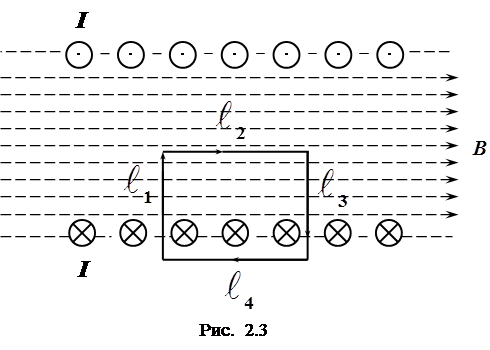
Для вычисления индукции внутри соленоида по обмотке которого идет ток I, можно воспользоваться законом полного тока. Для этого вычислим сначала циркуляцию вдоль замкнутого контура L, который в данном случае для упрощения суммирования удобно взять в виде прямоугольника, как показано на рис. 2.3 (закон полного тока справедлив для контура любой формы).

Тогда циркуляция распадается на четыре составные части:

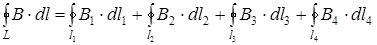(2.5)

Из рис. 2.3 видно, что суммирование вдоль участков l₁, l₃ и l₄ равно нулю, поскольку вектор индукции в этих случаях либо перпендикулярен отрезкамdl_i, либо равен нулю (вне соленоида). Таким образом,

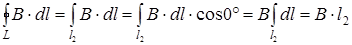(2.6)

где учтено, что величина и направление вектора B на участке l₂ внутри соленоида для всех dl_i одинаковы.

Пусть на единицу длины соленоида приходится n витков. Тогда контур L будет охватывать N=n·l₂проводников с током I, а значит

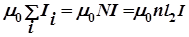. (2.7)

Приравнивая (2.6) и (2.7), в соответствии с законом полного тока, получим:

В = μ₀nI (2.8)

3. Метод измерений

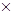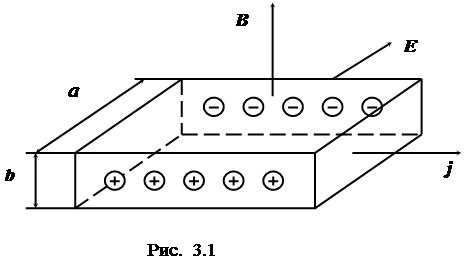
Для экспериментального исследования индукции магнитного поля на оси соленоида в настоящей работе используется метод, основанный на явлении Холла. Если через проводящую пластинку с поперечным сечением a b пропустить ток плотностью j и поместить ее в поперечное магнитное поле с индукцией B, то на движущиеся носители зарядов будет действовать сила Лоренца. В результате на одной грани пластинки будут скапливаться положительные, а на другой — отрицательные заряды. Таким образом, возникает добавочное электрическое поле, напряженность которого E перпендикулярна векторамB и j (рис. 3.1). Возникающая при этом разность потенциалов называется ЭДС Холла. Величина Δφ между боковыми гранями пропорциональна величине тока i и индукции В:

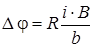(3.1)

Коэффициент пропорциональности R называется постоянной Холла. В работе используется полупроводниковый датчик Холла марки ДХГ-2 с управляющим током i = 12 мА. Поскольку линии магнитной индукции внутри соленоида направлены вдоль оси, то датчик Холла располагается на торце специального штока, вставляемого в соленоид. Для измерения положения датчика внутри соленоида на боковой грани штока нанесена миллиметровая шкала.

4. Требования к технике безопасности

1. Прежде чем приступить к работе, внимательно ознакомьтесь с заданием и оборудованием.

2. Проверьте заземление лабораторной установки и изоляцию токонесущих проводов.

3. Немедленно сообщите преподавателю или лаборанту о замеченных неисправностях.

4. Не загромождайте свое рабочее место оборудованием, не относящимся к выполняемой работе.

5. Не оставляйте без присмотра свою лабораторную установку, это может привести к несчастному случаю.

6. По окончанию работ приведите в порядок свое рабочее место. Обесточьте все лабораторные приборы.

7. Запрещается уходить из лаборатории без разрешения преподавателя.

5. Порядок выполнения работы

Задание 1. Определение зависимости магнитной индукции в средней точке на оси соленоида и тарировка датчика Холла.

Таблица 5.1

№	Ic, A	Δφ, В	B, Тл	R, В·м/Тл·А
…

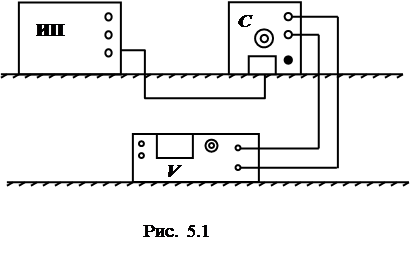
1. Собрать схему, изображенную на рис. 5.1.

2. Поставить шток с датчиком Холла в среднее положение на оси соленоида («0» по шкале).

3. Включить источник питания и цифровой вольтметр в сеть. Измерить ЭДС Холла в центре соленоида для токов 0,5; 1,0; 1,5; 2,0; 2,5 А. Данные занести в табл. 5.1.

4. Вычислить индукцию магнитного поля по формуле (2.8), полагая n = 17·10³ витков/м; данные занести в табл. 5.1.

5. Вычислить значение постоянной Холла R для каждого измерения по формуле (3.1); данные занести в табл. 5.1. Найти среднее значение R.

6. Построить график зависимости Δφ = f(I_c) по данным табл. 5.1.

Задание 2. Исследование зависимости индукции магнитного поля от координаты Z вдоль оси соленоида, отсчитываемой от средней точки.

1. Установить величину тока в катушке по указанию преподавателя.

2. Перемещая шток с датчиком Холла с интервалом ΔZ=1 см измерить ЭДС Холла вдоль всей оси соленоида. Полученные данные занести в табл. 5.2.

Таблица 5.2

Ток соленоида Ic = … A
Z, мм						…
Δφ, В
В, Тл

3. Вычислить индукцию поля В для каждого положения датчика Холла по формуле (3.1). При расчете использовать значение R, полученное в задании 1. Данные занести в табл. 5.2.

4. Построить график зависимости В от Z по данным табл. 5.2.

5. Повторить измерения и расчеты по пп. 2 – 4 для нового значения I_c, указанного преподавателем.

6. Для одного из полученных значений B рассчитать абсолютную и относительную погрешности измерения.

6. Требования к отчету

Отчет по лабораторной работе должен содержать:

1) название и номер лабораторной работы;

2) основные формулы для выполнения работы;

3) таблицы с результатами измерений и вычислений;

4) графики на миллиметровой бумаге;

5) расчеты погрешностей измерений;

6) выводы к работе.

7. Контрольные вопросы

1. Какие существуют характеристики магнитного поля?

2. Как определяется величина и направление вектора магнитной индукции магнитного поля?

3. Как вычисляется циркуляция вектора магнитной индукции?

4. Почему магнитное поле является вихревым?

5. Как формулируется закон полного тока? Какие величины и как он объединяет?

6. Как используется закон полного тока при расчете магнитного поля внутри соленоида?

7. Какое явление лежит в основе экспериментального определения магнитного поля соленоида?

Список литературы

1. Савельев И.В. Курс общей физики. T. 2. – М.: Наука. Физмат, 1998.

2. Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высшая школа, 1999.