Основной закон релятивистской динамики материальной точки

Согласно представлениям классической механики, масса тела есть величина постоянная. Однако в конце XIX столетия на опытах с быстро движущимися электрона­ми было установлено, что масса тела за­висит от скорости его движения, а имен­но возрастает с увеличением скорости по закону

m = 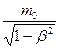, ( β = υ/c ) (5.10)

где т₀ - масса покояматериальной точ­ки, т. е. масса, измеренная в той инерциальной системе отсчета, относительно ко­торой материальная точка находится в по­кое; с - скорость света в вакууме; т - масса точки в системе отсчета, относи­тельно которой она движется со скоростью υ. Из принципа относительности Эйнштейна, утверждающего инва­риантность всех законов природы при пе­реходе от одной инерциальной системы отсчета к другой, следует условие инвари­антности уравнений физических законов относительно преобразований Лоренца. Основной закон динамики Ньютона

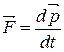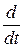= (mυ) (5.11)

оказывается также инвариантным по от­ношению к преобразованиям Лоренца, ес­ли в нем справа стоит производная по времени от релятивистского импульса.

Учитывая, что релятивистский импульс материальной точки

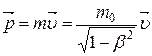, (5.12)

основной закон релятивистской дина­микиматериальной точки имеет вид

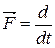
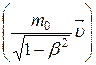. (5.13)

Отметим, что уравнение (5.11) внешне совпадает с основным уравнением ньютоновской механики. Однако физический смысл его другой: справа стоит производная по времени отрелятивистское импульса, определяемого формулой(5.12). Таким образом, уравнение (5.13) инвариантно по отношению к преобразованиям Лоренца и, следова­тельно, удовлетворяет принципу относи­тельности Эйнштейна. Следует учитывать, что ни импульс, ни сила не являются инва­риантными величинами. Более того, в об­щем случае ускорение не совпадает по направлению с силой.

В силу однородности пространства в релятивистской механике вы­полняется закон сохранениярелятивист­ского импульса:релятивистский импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени.

Анализ формул (5.10), (5.12) и (5.13) показывает, что при скоростях, значитель­но меньших скорости света, уравне­ние (5.13) переходит в основной закон классической механики. Следо­вательно, условием применимости законов классической (ньютоновской) механики является условие υ << c. Законы классиче­ской механики получаются как следствие теории относительности для предельного случая υ << c.Таким образом, классическая механика-это механика макротел, движущихся с малыми скоро­стями (по сравнению со скоростью света в вакууме).

Экспериментальное доказательство за­висимости массы от скорости (5.10) явля­ется подтверждением справедливости спе­циальной теории относительности. На основании этой зависимости про­изводятся расчеты ускорителей элементарных частиц.