И 24.Статистика равновесных носителей заряда в полупроводниках .Электронно-дырочная теплоемкость полупроводников.

В случае полупроводника вопрос о распределении носителей заряда несколько усложняется. Дело в том, что в полупроводнике носители заряда возникают в результате возбуждения электронов из валентной зоны в зону проводимости (разрыва валентных связей). В результате такого перехода мы получаем электрон в валентной зоне и пустое место (дырку) в зоне проводимости. Валентные электроны соседних атомов могут захватываться на пустое место. Таким образом, дырка перемещается по кристаллу, и, соответственно, дает вклад в его термодинамические характеристики. Вероятность возбуждения электрона в валентную зону , очевидно, изменяется с температурой как , где - ширина запрещенной зоны. Поэтому число электронов в зоне проводимости, и число дырок в валентной зоне существенно зависит от температуры. Кроме того, для того, чтобы повысить число носителей заряда, полупроводники легируют. Поэтому при описании полупроводника мы должны учитывать также и примеси. Ясно, что концентрации носителей заряда должны существенным образом зависеть от концентрации примесей, и отношения энергии их ионизации к температуре.

Таким образом, вычисление химического потенциала полупроводника при заданном числе носителей в зонах становится бессмысленным. Поэтому в полупроводниках уравнение для определения химического потенциала нужно писать из несколько иных соображений.

Рассмотрим собственный полупроводник (без примесей). В этом случае электроны проводимости и дырки в валентной зоне появляются только парами. Поэтому число электронов в зоне проводимости и дырок в валентной зоне одинаково

. (1)

Равенство (11) можно использовать как уравнение для химического потенциала. Действительно, число электронов и дырок даются выражениями

. (2)

и

. (3)

Здесь мы учли, что вероятность того, что в состоянии нет электрона (среднее число дырок в этом состоянии) есть . Таким образом, подставив эти интегралы в (1) мы получим уравнение для химического потенциала.

Ясно, что в состоянии равновесия дырки будут расположены главным образом вблизи потолка валентной зоны. Поэтому при вычислении достаточно рассмотреть только эти состояния. Для простоты валентную зону также будем считать зону проводимости невырожденной, а эффективную массу изотропной

, (4)

где - масса дырки вблизи потолка валентной зоны.

Как было получено на прошлой лекции, плотность состояний невыроженной зоны проводимости с изотропным параболическим законом дисперсии имеет вид

, (5)

Легко сообразить, что плотность состояний вблизи потолка валентной зоны будет получаться из (5) заменой на и на . Таким образом,

. (6)

Соответственно, для числа электронов проводимости и дырок получаем

. (7)

и

. (8)

Здесь мы ввели обозначения и .

Как мы видели на прошлой лекции, при

. (9)

Таким образом, при абсолютном нуле

. (10)

и

. (11)

Поскольку при абсолютном нуле свободных носителей нет , то из (10) и (11) следует, что и . Следовательно, . Таким образом, мы видим, что химический потенциал лежит в запрещенной зоне.

Рассмотрим теперь случай достаточно низких температур, при которых . Тогда получаем

. (12)

и

. (13)

Учитывая, что

, (14)

получаем

. (15)

и

. (16)

Здесь мы обозначили

(18)

и

(19)

Величины (18) и (19) называются эффективными плотностями состояний зоны проводимости и валентной зоны соответственно.

Таким образом, уравнение (1) для химического потенциала принимает вид

. (20)

Отсюда для химического потенциала получаем

. (21)

Таким образом, мы видим, что при абсолютном нуле температуры химический потенциал в собственном полупроводнике находится посередине запрещенной зоны. Энергии краев зон зависят от температуры. Если выбрать начало отсчета энергии в середине запрещенной зоны при любой температуре, то хим. потенциал – линейная функция температуры. С ростом температуры он приближается к той зоне, в которой эффективная масса плотности состояний меньше. Это происходит потому что для обеспечения равенства концентрации электронов и дырок необходимо чтобы химический потенциал располагался ближе к зоне с меньшей плотностью состояний.

Подставляя (21) в (15) и (16), находим равновесные значения концентраций свободных носителей заряда

. (22)

Таким образом, мы видим, что, как и следовало ожидать, число носителей в собственном полупроводнике, пропорционально вероятности возбуждения электрона из валентной зоны в зону проводимости.

В случае примесных полупроводников мы должны учесть, что электроны в зоне проводимости могут появляться за счет перехода с донорных примесных уровней, а дырки в валентной зоне за счет переходов электронов на акцепторные уровни. Поэтому в этом случае уравнение на химический потенциал мы должны писать как

. (23)

Здесь и - число заряженных акцепторов и доноров соответственно.

Задача о вычислении концентрации электронов на примесных уровнях довольно непростая. Ее мы рассмотрим на отдельном семинарском занятии. Пока же для качественных оценок мы будем использовать самое простое приближение – будем считать, что каждая примесь имеет один невырожденный уровень энергии и соответственно. Тогда

(24)

и

, (25)

где и - концентрация акцепторов и доноров соответственно.

Определим теперь положение хим. потенциала в полупроводнике, в котором имеется только один сорт примеси. Пусть это будут доноры. Здесь возможны два случая. Если температура не очень велика, тогда электроны в зоне проводимости будут появляться в основном за счет термоионизации доноров. В этом случае концентрацией дырок можно пренебречь и условие (23) приобретает вид

. (26)

При достаточно высоких температурах концентрация электронов в зоне проводимости, пришедших из валентной зоны может оказаться больше, чем концентрации доноров. В этом случае полупроводник будет вести себя как собственный.

Найдем химический потенциал в первом случае, когда справедливо (26). В случае невырожденного полупроводника (в котором ) число электронов в зоне проводимости дается (15). Выражая химический потенциал через концентрацию электронов в зоне проводимости

. (27)

, запишем (26) в виде

, (28)

где

. (29)

Решая квадратное уравнение (28) находим концентрацию электронов проводимости

. (30)

Рассмотрим два предельных случая. Пусть температура настолько низка, что выполняетсяусловие Тогда из (29) получаем

, (31)

где энергия ионизации основного состояния донора. Из (31) видно, что при низких температурах зависимость электронной концентрации от температуры определяется в основном экспонентой с показателем равным половине энергии ионизации деленной на температуру. Поэтому, измеряя зависимость концентрации от температуры можно найти энергию ионизации донора. Подставляя (21) в (27), находим зависимость химического потенциала от температуры

. (32)

При концентрации доноров , и температуре Т=300 К, величина, стоящая под знаком логарифма в (32), порядка , т.е. второе слагаемое порядка 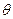. Это означает, что химический потенциал проходит примерно посередине между нижним краем зоны и донорным уровнем.

Рассмотрим теперь противоположный предельный случай, когда Он соответствует достаточно высоким температурам, когда эффективная плотность состояний зоны проводимости велика по сравнению с концентрацией доноров, но температура должна быть не слишком велика для того чтобы концентрация дырок была много меньше концентрации доноров. Проводя в (30) разложение по малому параметру, получаем

, (33)

т.е. электроны со всех доноров ушли в зону проводимости. Для химического потенциала в этом случае получаем

.. (34)

Легко видеть, что логарифм в (34) отрицательный, и химический потенциал расположен ниже донорного уровня.

Рассмотрим теперь случай компенсированного полупроводника. Компенсированным называется полупроводник, в котором имеются как доноры, так и акцепторы. Пусть . Будем опять рассматривать случай не слишком высоких температур, когда можно пренебречь дырками в валентной зоне. В этом случае все акцепторы захватывают электроны с доноров и заряжаются отрицательно. Этот процесс энергетически выгоден с точки зрения термодинамики. Оставшиеся на донорах электроны имеют возможность уйти в зону проводимости. Условие (23) в этом случае имеет вид

. (35)

Поступая также, как при получении (28), уравнение (35) запишем в виде

, (36)

Отсюда

. (37)

Рассмотрим опять два предельных случая. В случае низких температур разлагая в (37) корень в ряд Тейлора получим

. (38)

Как видно, при низких температурах зависимость электронной концентрации от температуры определяется в основном экспонентой с показателем равным энергии ионизации деленной на температуру.

Соответственно, для химического потенциала полуяаем

. (39)

Отметим, что при абсолютном нуле температуры химический потенциал равен энергии основного состояния донора. Так должно быть, поскольку при нулевой температуре хим. потенциал отделяет занятые состояния от пустых. В рассматриваемом случае при нулевой температуре часть доноров не имеет электронов, а в оставшейся части электрон занимает основное состояние донора.

В случае высоких температур выражение (37) опять можно разложить в ряд Тейлора. В результате получаем

, (40)

т.е. все оставшиеся электроны после ухода на акцепторы попадают в зону проводимости. Зависимость хим. потенциала от температуры в этом случае имеет вид

. (42)

Вычислим теперь теплоемкость электронной подсистемы полупроводника. Для простоты рассмотрим собственный полупроводник. Внутренняя энергия электронов проводимости и валентных электронов

. (43)

Здесь первая сумма есть внутренняя энергия электронов в зоне проводимости, а вторая – внутренняя энергия электронов в валентной зоне. Совершая во второй сумме тождественное преобразование

, (44)

получаем

. (43)

Величина есть энергия полностью заполненной валентной зоны. Для данного полупроводника она есть константа, не зависящая от температуры. Примем эту константу за нуль энергии. Тогда

. (44)

Как видно, внутренняя энергия складывается из двух частей – внутренней энергии электронов в зоне проводимости, и внутренней энергии частиц с энергией , распределенных также как и пустые места в валентной зоне (т.е. дырок).

Записывая выражение (44) через плотность состояний и воспользовавшись (5) и (6), находим

, (45)

где

. (46)

Для упрощения вычислений рассмотрим невырожденный полупроводник. Тогда концентрация носителей в зонах дается выражением (22), а для интеграла (46) имеем

. (47)

Интеграл (47) заменой сводится к интеграл . Вычислив таким образом этот интеграл, получим

. (48)

Подставляя (48) в выражение для внутренней энергии (45), и используя (20) и (21), получим

. (49)

Дифференцируя (49) по температуре, находим электронно-дырочную теплоемкость, отнесенную к единице объема

, (50)

где

. (51)

Формула (50) справедлива при . Иначе нужно учитывать вырождение свободных электронов и дырок. Легко показать, что наибольшее значение получается при . Тогда по порядку величины .

Теплоемкость 1см³ при температурах выше дебаевской по порядку величины равна , где - концентрация атомов. Таким образом, .

Аналогичные соотношения имеют место и в случае примесных полупроводников. Таким образом, электронно-дырочная теплоемкость в полупроводниках всегда очень мала по сравнению с теплоемкостью кристаллической решетки.