Электромагнитные колебания и волны

Электромагнитные колебания – это периодические изменения со временем электрических и магнитных величин в электрической цепи.

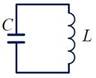При колебаниях происходит непрерывный процесс превращения энергии системы из одной формы в другую. В случае колебаний электромагнитного поля обмен может идти только между электрической и магнитной составляющей этого поля. Простейшей системой, где может происходить этот процесс, является колебательный контур. Идеальный колебательный контур (LC-контур) — это электрическая цепь, состоящая из катушки индуктивностью L и конденсатора емкостью C.

В отличие от реального колебательного контура, который обладает электрическим сопротивлением R, электрическое сопротивление идеального контура всегда равно нулю. Следовательно, идеальный колебательный контур является упрощенной моделью реального контура.

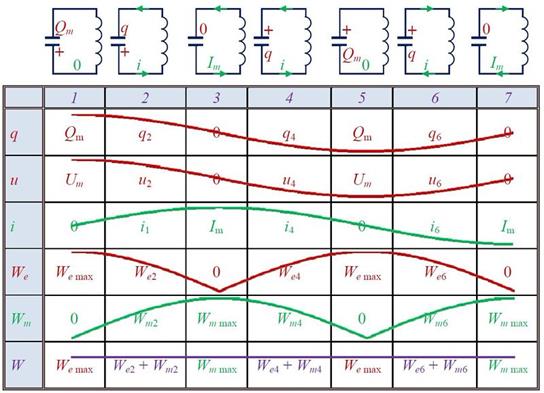
Рассмотрим процессы, которые возникают в колебательном контуре. Для выведения системы из положения равновесия зарядим конденсатор так, что на его обкладках будет заряд Q_m. Из формулы, связывающей заряд конденсатора и напряжение на нём, находим значение максимального напряжения на конденсаторе 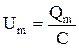. Тока в цепи в этом момент времени нет, т.е. 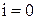. Сразу после зарядки конденсатора под действием его электрического поля в цепи появится электрический ток, величина которого будет увеличиваться с течением времени. Конденсатор в это время начнет разряжаться, т.к. электроны, создающие ток, (напоминаю, что за направление тока принято направление движения положительных зарядов) уходят с отрицательной обкладки конденсатора и приходят на положительную. Вместе с зарядом q будет уменьшаться и напряжение u. При увеличении силы тока через катушку возникнет ЭДС самоиндукции, препятствующая изменению (возрастанию) силы тока. Вследствие этого, сила тока в колебательном контуре будет возрастать от нуля до некоторого максимального значения не мгновенно, а в течение некоторого промежутка времени, определяемого индуктивностью катушки. Заряд конденсатора q уменьшается и в некоторый момент времени становится равным нулю (q = 0, u = 0), сила тока в катушке достигнет максимального значения I_m. Без электрического поля конденсатора (и сопротивления) электроны, создающие ток, продолжают свое движение по инерции. При этом электроны, приходящие на нейтральную обкладку конденсатора, сообщают ей отрицательный заряд, электроны, уходящие с нейтральной обкладки, сообщают ей положительный заряд. На конденсаторе начинает появляться заряд q (и напряжение u), но противоположного знака, т.е. конденсатор перезаряжается. Теперь новое электрическое поле конденсатора препятствует движению электронов, поэтому сила тока начинает убывать. Опять же это происходит не мгновенно, поскольку теперь ЭДС самоиндукции стремится скомпенсировать уменьшение тока и «поддерживает» его. А значение силы тока I_m оказывается максимальным значением силы тока в контуре. Далее сила тока становится равной нулю, а заряд конденсатора достигнет максимального значения Q_m (U_m). И снова под действием электрического поля конденсатора в цепи появится электрический ток, но направленный в противоположную сторону, величина которого будет увеличиваться с течением времени. А конденсатор в это время будет разряжаться. И так далее.

Так как заряд на конденсаторе q (и напряжение u) определяет его энергию электрического поля W_e 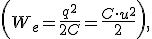а сила тока в катушке — энергию магнитного поля Wm 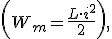то вместе с изменениями заряда, напряжения и силы тока, будут изменяться и энергии.

Электромагнитные колебания – это колебания электрического заряда, силы тока, напряжения, связанные с ними колебания напряженности электрического поля и индукции магнитного поля.

Свободными называются такие колебания, которые возникают в замкнутой системе вследствие отклонения этой системы от состояния устойчивого равновесия. Применительно к колебательному контуру это означает, что свободные электромагнитные колебания в колебательном контуре возникают после сообщения энергии системе (зарядки конденсатора или пропускания тока через катушку).

Циклическая частота и период колебаний в колебательном контуре определяются по формулам: , .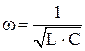

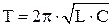Максвелл теоретически предсказал существование электромагнитных волн, т.е. переменного электромагнитного поля, распространяющегося в пространстве с конечной скоростью, и создал электромагнитную теорию света.

Электромагнитная волна – это распространение в пространстве с течением времени колебаний векторов 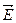и .

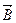Если в какой-либо точке пространства возникает быстро меняющееся электрическое поле, то оно в соседних точках вызывает появление переменного магнитного поля, которое, в свою очередь возбуждает появление переменного электрического поля и т.д. Чем быстрее меняется магнитное поле (больше 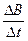), тем интенсивнее возникающее электрическое поле Е и наоборот. Таким образом, необходимым условием образования интенсивных электромагнитных волн является достаточно высокая частота электромагнитных колебаний.

Из уравнений Максвелла следует, что в свободном пространстве, где нет токов и зарядов (j=0, q=0) электромагнитные волны поперечны, т.е. вектор скорости волны 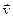перпендикулярен векторам 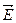и 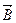, и векторы 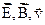образуют правовинтовую тройку.

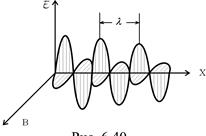Модель электромагнитной волны показана на рисунке. Это плоская линейно поляризованная волна. Длина волны 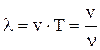, где Т – период колебаний, 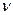— частота колебаний. В оптике и радиофизике модель электромагнитной волны выражается через векторы 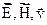. Из уравнений Максвелла следует 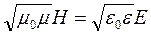. Это означает, что в бегущей плоской электромагнитной волне колебания векторов 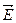и 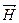происходят в одинаковой фазе и в любой момент времени электрическая энергия волны равна магнитной.

Скорость электромагнитной волны в среде 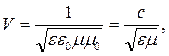где V – скорость электромагнитной волны в данной среде, 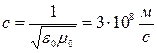, с – скорость электромагнитной волны в вакууме, равная скорости света.

Выведем волновое уравнение.

Как известно из теории колебаний, уравнение плоской волны, распространяющейся вдоль оси x 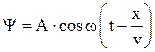, где 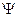– колеблющаяся величина (в данном случае E или H), v – скорость волны, ω – циклическая частота колебаний.

Таким образом, уравнение волны 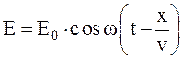Продифференцируем его дважды по t и по x. 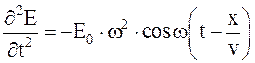, 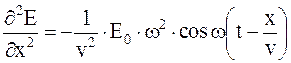. Отсюда получаем 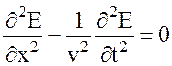. Аналогично можно получить 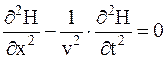. В общем случае, когда волна распространяется в произвольном направлении, эти уравнения следует записать в виде: 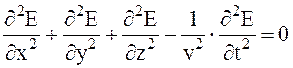, 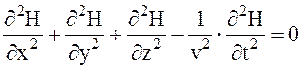. Выражение 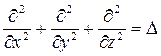называется оператором Лапласа. Таким образом,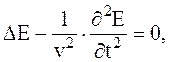 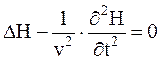. Эти выражения называются волновыми уравнениями.

В колебательном контуре происходит периодическое превращение электрической энергии конденсатора 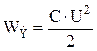в магнитную энергию катушки индуктивности 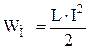. Период колебаний 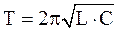. При этом излучение электромагнитных волн мало, т.к. электрическое поле сосредоточено в конденсаторе, а магнитное – внутри соленоида. Чтобы сделать излучение заметным, нужно увеличить расстояние между обкладками конденсатора С и витками катушки L. При этом объем, занимаемый полем, увеличится, L и С – уменьшатся, т.е. частота колебаний возрастет.

Экспериментально электромагнитные волны впервые получил Герц (1888 г.) при помощи изобретенного им вибратора. Попов (1896 г.) изобрел радио, т.е. использовал электромагнитные волны для передачи информации.

Для характеристики энергии, переносимой электромагнитной волной, вводится вектор плотности потока энергии. Он равен энергии, переносимой волной за 1 секунду через единичную площадку, перпендикулярную вектору скорости 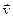. 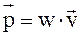где 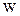– объемная плотность энергии, v – скорость волны.

Объемная плотность энергии 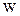складывается из энергии электрического поля и магнитного поля .

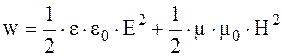Учитывая 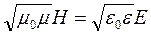, можно записать 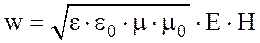. Отсюда плотность потока энергии 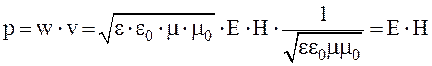. Поскольку 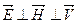, получаем 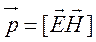. Это вектор Умова-Пойнтинга.

Шкала электромагнитных волн – это расположение диапазонов электромагнитных волн в зависимости от их длины волны λ и соответствующих свойств.

1) Радиоволны. Длина волны λ от сотен километров до сантиметров. Для генерирования и регистрации служит радиоаппаратура.

2) Микроволновая область λ от 10 см до 0,1 см. Это радиолокационный диапазон или диапазон СВЧ (сверхвысоких частот). Для генерирования и регистрации этих волн существует специальная аппаратура СВЧ.

3) Инфракрасная (ИК) область λ~1мм 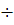800 нм. Источники излучения – нагретые тела. Приемники – тепловые фотоэлементы, термоэлементы, болометры.

4) Видимый свет, воспринимаемый человеческим глазом. λ~0,76 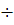0,4 мкм.

5) Ультрафиолетовая (УФ) область λ~400 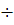10 нм. Источники – газовые разряды. Индикаторы – фотопластинки.

6) Рентгеновское излучение λ~10нм 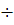10^-3нм. Источники – рентгеновские трубки. Индикаторы – фотопластинки.

7) γ-лучи λ<10пм. Источники – радиоактивные превращения. Индикаторы – специальные счетчики.