Энергия и волновые функции атома водорода

Рассмотрим систему, состоящую из электрона е, который движется в кулоновском поле ядра с зарядом Ze . Такую систему называют водородоподобной. При Z =1 это атом водорода, при Z =2 – однократно ионизованный атом гелия - ион 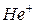и т.д.

Потенциальная энергия взаимодействия электрона с ядром равна

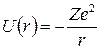, (5.1)

где r - расстояние между электроном и ядром, которое будем полагать точечным и неподвижным.

Уравнение Шрёдингера будет иметь вид

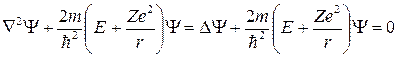. (5.2)

Поле, в котором движется электрон, является центрально-симметричным, т.е. зависит только от 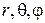. Поэтому решение уравнения (5.2) целесообразно проводить в сферической системе координат. Оператор Лапласа в этой системе запишется

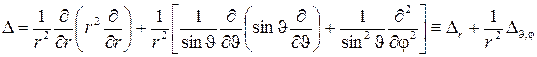. (5.3)

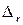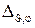Здесь и − радиальная и угловая части лапласиана соответственно.

Тогда (5.2) перепишется

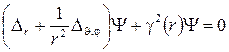, (5.4)

где 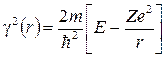(5.5)

зависит только от r.

Угловые 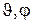и радиальные r координаты независимы и решение можно искать в виде 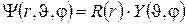. Тогда 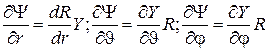и уравнение (5.4) после умножения на 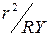и перегруппировки слагаемых примет вид

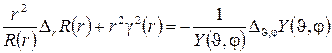. (5.6)

Поскольку в левой части этого уравнения стоит величина, зависящая только от радиальной, а в правой – только от угловых координат, то это равенство может иметь место только тогда, когда обе его части равны одной и той же постоянной 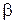. Таким образом, из (5.6) получаем два уравнения для радиальной и угловой частей волновой функции:

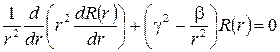, (5.7)

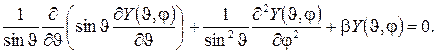(5.8)

Займемся анализом уравнения (5.8), заметив, что оно не содержит потенциальную энергию. Поэтому результаты, получаемые из него, имеют универсальный характер и описывают общие свойства поведения частицы в любом центральном поле сил. Угловые координаты 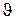и 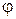также являются независимыми и поэтому функцию 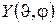можно представить в виде

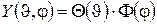. (5.9)

Подставив это выражение в (5.8), получим

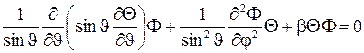. (5.10)

Домножив (5.10) на 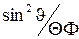и проведя перегруппировку слагаемых, зависящих от соответствующих переменных, получим

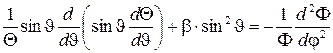. (5.11)

В соотношении (5.11) частные производные заменены полными, так как функци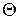и и 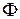зависят каждая только от одной переменной. Поскольку в левой и правой частях (5.11) стоят функции, зависящие от разных переменных, данное равенство может иметь место, если обе его части будут равны одной и той же постоянной 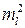. Тогда из (5.11) получаем два уравнения для одной переменной каждое:

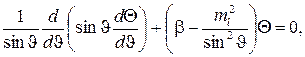(5.12)

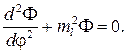(5.13)

Очевидно, что решением уравнения (5.13) является функция

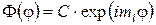, (5.14)

где С – произвольная постоянная. Поскольку 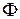должна быть однозначной функцией угла 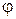, она не должна меняться при изменении угла 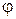на угол кратный 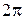. Следовательно

,

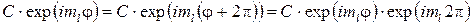откуда 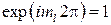. Величины удовлетворяющие этому условию, образуют ряд допустимых квантовых значений:

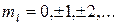(5.15)

Число , удовлетворяющее условию (5.15), называют магнитным квантовым числом.

Обратимся теперь к уравнению (5.12).Из курса математики известно, что конечные во всей области изменения переменной 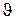решения (5.12) существуют лишь при определенных значениях параметра 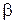, равных 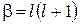. Величина l, получившая в квантовой механике название азимутального квантового числа, при этом может принимать лишь неотрицательные целые значения:

l = 0, 1, 2,… (5.16)

Решением уравнения (5.12) является специальная функция, функция 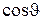, называемая полиномом Лежандра − .

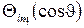Таким образом, угловая часть волновой функции зависит от двух целочисленных параметров (квантовых чисел) 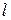и .

Оределим теперь радиальную часть волновой функции 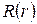. Учитывая, что 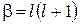, уравнение (5.7) перепишем

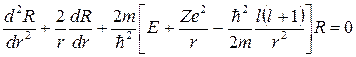. (5.18)

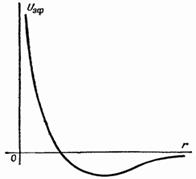(5.18) можно трактовать как уравнение, описывающее одномерное движение в потенциальном поле, с эффективной потенциальной энергией 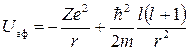(рис.5.1). Отсюда видно, что при Е < 0 мы имеем «потенциальную яму» и следует ожидать, что движение будет периодическим, а значения энергии квантованными. При Е > 0 движение ограничено только с одной стороны потенциальным барьером. В этом случае спектр собственных значений энергии будет сплошным.

Мы будем рассматривать только случай Е< 0. Рис.5.1 Введем обозначения 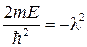; 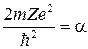(5.19)

и перепишем уравнение (5.18)

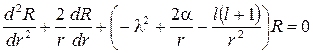(5.20)

и рассмотрим асимптотический случай, когда r очень велико. В этом случае уравнение (5.20) перепишется

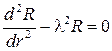. (5.21)

Его решение .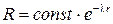

Можно показать, что в общем случае решение уравнения (5.20) имеет вид

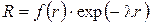, (5.22)

где 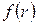- многочлен по степеням r. Точное значение функции R(r),которая зависит от двух целых положительных чисел n, l (квантовые числа) имеет вид:

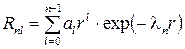, где 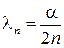. (5.23)

Тогда, принимая во внимание (5.19) можно получить разрешенные значения энергии атома 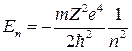. (5.24)

Приведем, например, значения энергии и радиальной части волновой функции для двух состояний:

п = 1 – основное состояние ; ;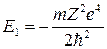

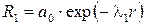п = 2 – первое возбужденное ; .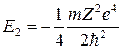

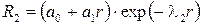Из (5.19) и (5.23) следует, что для атома водорода ( Z =1) 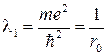, где 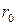− первый боровский радиус.

Таким образом, квантовая механика приводит к таким же значениям энергии, что и теория Бора. Однако в квантовой механике эти значения получаются как следствие ее основных положений. Бору же для получения такого результата пришлось вводить специальные дополнительные предположения.

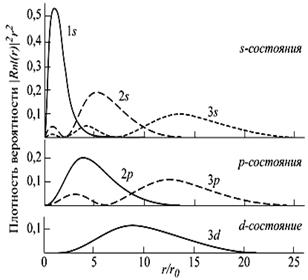Получив выражение для волновой функции, мы можем найти вероятность нахождения электрона в определенной точке пространства. Для атома водорода вероятность нахождения электрона в радиальном слое толщины dr на расстоянии r от ядра 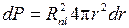приведена на рис.5.2. Расстояния даны в боровских радиусах 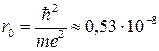см. Цифры на кривых означают квантовое число п, буквы квантовые числа l (s соответствует l = 0; p - l = 1; d – l =2). Из рисунка видно, что в основном состоянии 1s максимальна вероятность обнаружить элекРис.5.2 трон на расстоянии первого боровского

радиуса.

Лекция 6