Общие методические указания к решению задач и выполнению контрольных работ
Содержание
Введение. 2
1. Содержание курса физики. 3
2 ЛИТЕРАТУРА.. 9
3 ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ И ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ. 10
4 Основные формулы.. 12
5 Таблицы вариантов. 36
6 Задачи для контрольных работ. 41
ПРИЛОЖЕНИЯ.. 92
ЛИТЕРАТУРА
1. Трофимова Т.И. Курс физики. - М.: Высшая школа, 1985.
2. Детлаф А.А., Яворский Б.М., Милковская Л.Б. Курс физики. - М.: Высшая школа, 1973 – 1979. - Т. 1, 2, 3.
3. Зисман Г.А., Тодес О.М. Курс общей физики. - М.: Наука, 1972 - 1974. - Т. 1, 2, 3.
4. Савельев И.В. Курс общей физики. - М.: Наука, 1977 - 1979. - Т. 1, 2, 3.
5. Сивухин Д.В. Общий курс физики. - М.: Наука, 1977-1980.- Т. 1, 2, 3, 4.
6. Епифанов Г.И. Физика твердого тела. Учеб. пособие для втузов. Изд. 2—е, перераб. и доп. М., Высш. шк., 1977. 288 с.: ил
7. Волькенштейн В.С. Сборник задач по общему курсу физики. - М.: Наука, 1979.
8. Чертов А. Г., Воробьев А. А. Задачник по физике. - М.: Высшая школа, 1987.
9. Иродов И.Е. Задачи по квантовой физике: Учебное пособие для физ. спец. вузов. – М.: Высш. шк., 1991. – 175 с.: ил.
10. Пинский А.А. Задачи по физике. - М.: Высш. шк., 1985.
11. Трофимова Т.И., Павлов З.Г. Сборник задач по курсу физики с решениями: Учебное пособие для вузов. - М.: Высш. шк., 1999. – 591 с.: ил.
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ И ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ
1. За время изучения курса общей физики студент-заочник должен представить в учебное заведение в зависимости от специальности от четырех до восьми контрольных работ.
2. Номера задач, которые студент должен включить в свою контрольную работу, определяются по таблицам вариантов.
3. Контрольные работы нужно выполнять чернилами в школьной тетради.
4. Условия задач в контрольной работе надо переписать полностью без сокращений. Для замечаний преподавателя на страницах тетради оставлять поля.
5. Высылать на рецензию следует одновременно не более одной работы. Во избежание одних и тех же ошибок очередную работу следует высылать только после получении рецензии на предыдущую.
6. Если контрольная работа при рецензировании не зачтена, студент обязан представить ее на повторную рецензию, включив в нее те задачи, решения которых оказались неверными. Повторную работу необходимо представить в месте с незачтенной.
7. Зачтенные контрольные работы предъявляются экзаменатору. Студент должен быть готов во время экзамена дать пояснения по существу решения задач, входящих в контрольные работы.
8. Решения задач следует сопровождать краткими, но исчерпывающими пояснениями; в тех случаях, когда это возможно, дать чертеж, выполненный с помощью чертежных принадлежностей.
9. Решать задачу надо в общем виде, т.е. выразить искомую величину в буквенных обозначениях величин, заданных в условии задачи. При таком способе решения не производятся вычисления промежуточных величин.
10. После получения расчетной формулы для проверки правильности ее следует подставить в правую часть формулы вместо символов величин обозначения единиц этих величин, произвести с ними необходимые действия и убедиться в том, что полученная при этом единица соответствует искомой величине. Если такого соответствия нет, то это означает, что задача решена неверно.
11. Числовые значения величин при подстановке их в расчетную формулу следует выражать только в единицах СИ. В виде исключения допускается выражать в любых, но одинаковых единицах числовые значения однородных величин, стоящих в числителе и знаменателе дроби и имеющих одинаковые степени.
12. При подстановке в расчетную формулу, а также при записи ответа числовые значения величин следует записывать как произведение десятичной дроби с одной значащей цифрой перед запятой на соответствующую степень десяти. Например, вместо 3520 надо записать 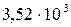 , вместо 0,00129 записать
, вместо 0,00129 записать 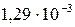 и т.п.
и т.п.
13. Вычисления по расчетной формуле надо проводить с соблюдением правил приближенных вычислений. Как правило, окончательный ответ следует записывать с тремя значащими цифрами. Это относится и к случаю, когда результат получен с применением калькулятора.
Основные формулы
Классическая механика.Кинематическое уравнение движения материальной точки (центра масс твердого тела) вдоль оси х
x = f(t),
где f(t) – некоторая функция времени.
Проекция средней скорости на ось х
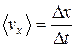
Средняя путевая скорость
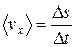
где ∆s – путь, пройденный точкой за интервал времени ∆t. Путь ∆s в отличие от разности координат ∆х = х2 – х1не может убывать и принимать отрицательные значения, т. е. ∆s ≥ 0.
Проекция мгновенной скорости на ось х
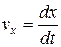 .
.
Проекция среднего ускорения на ось х
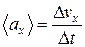 .
.
Проекция мгновенного ускорения на ось х
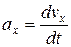 .
.
Кинематическое уравнение движения материальной точки по окружности
φ = f (f), r = R = const.
Модуль угловой скорости
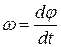 .
.
Модуль углового ускорения
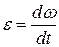 .
.
Связь между модулями линейных и угловых величин, характеризующих движение точки по окружности:
v = ωR, aτ = εR, ап = ω2R,
где v – модуль линейной скорости; aτ и ап – модули тангенциального и нормального ускорений; ω – модуль угловой скорости; ε – модуль углового ускорения; R – радиус окружности.
Модуль полного ускорения
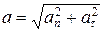 , или
, или 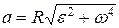 .
.
Угол между полным 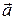 и нормальным
и нормальным 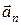 ускорениями
ускорениями
a = arc cos(an/a).
Кинематическое уравнение гармонических колебаний материальной точки
х = Acos (ωt + j),
где х – смещение; А – амплитуда колебаний; ω – угловая или циклическая частота; j – начальная фаза.
Циклическая частота w, период колебаний T и частота n связаны соотношениями
w = 2p/T = 2pn.
Скорость и ускорение материальной точки, совершающей гармонические колебания:
v = –Aωsin(ωt + j); а = –Aω2cos(ωt + j).
Сложение гармонических колебаний одного направления и одинаковой частоты:
а) амплитуда результирующего колебания
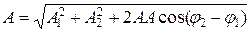 ;
;
б) начальная фаза результирующего колебания
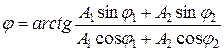 .
.
Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях,
х = А1соsωt; у = А2cos(ωt + φ):
а) 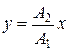 , если разность фаз j =0;
, если разность фаз j =0;
б) 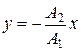 , еслиразность фаз j = ±π;
, еслиразность фаз j = ±π;
в) 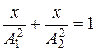 , если разность фаз j =±
, если разность фаз j =± 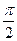 .
.
Период колебаний математического маятника
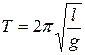 ,
,
где l – длина маятника, g – ускорение свободного падения.
Период колебаний пружинного маятника
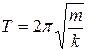 ,
,
где m – масса, k – жесткость пружины
Период колебаний физического маятника
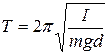 ,
,
где I – момент инерции маятника относительно оси качения, d – расстояние от оси до центра тяжести.
Уравнение плоской бегущей волны
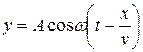 ,
,
где у – смещение любой из точек среды с координатой х в момент t; v – скорость распространения колебаний в среде.
Связь разности фаз ∆j колебаний с расстоянием ∆х между точками среды, отсчитанным в направлении распространения колебаний;
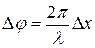 ,
,
где λ – длина волны.
Импульс материальной точки массой m, движущейся со скоростью 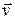 ,
,
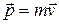 .
.
Второй закон Ньютона
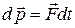 ,
,
где 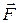 – результирующая сила, действующая на материальную точку.
– результирующая сила, действующая на материальную точку.
Силы, рассматриваемые в механике:
а) сила упругости
F = – kx,
где k – коэффициент упругости (в случае пружины – жесткость); х – абсолютная деформация;
б) сила тяжести
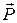 = m
= m 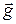 ;
;
в) сила гравитационного взаимодействия
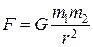 ,
,
где G – гравитационная постоянная; m1и т2 – массы взаимодействующих тел; r – расстояние между телами (тела рассматриваются как материальные точки). В случае гравитационного взаимодействия силу можно выразить также через напряженность 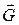 гравитационного поля:
гравитационного поля:
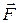 = m
= m 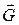 ;
;
г) сила трения (скольжения)
F = m×N,
где m – коэффициент трения; N – сила нормального давления.
Закон сохранения импульса
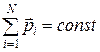 ,
,
или для двух тел (i=2)
m1 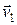 + m2
+ m2 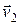 =m1
=m1 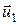 + m2
+ m2 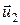 ,
,
где 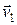 и
и 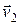 – скорости тел в момент времени, принятый за начальный;
– скорости тел в момент времени, принятый за начальный; 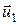 и
и 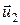 – скорости тех же тел в момент времени, принятый за конечный.
– скорости тех же тел в момент времени, принятый за конечный.
Кинетическая энергия тела, движущегося поступательно,
Eк = тv2/2, или Eк = р2/(2т).
Потенциальная энергия:
а) упругодеформированной пружины
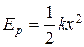 ,
,
где k – жесткость пружины; х – абсолютная деформация;
б) гравитационного взаимодействия
Ep = –Gm1m2/r,
где G – гравитационная постоянная; т1и т2 – массы взаимодействующих тел; r – расстояние между ними (тела рассматриваются как материальные точки);
в) тела, находящегося в однородном поле силы тяжести,
Ep = mgh,
где g – ускорение свободного падения; h – высота тела над уровнем, принятым за нулевой (формула справедлива при условии h<<R, где R – радиус Земли).
Закон сохранения механической энергии
Е = Eк + Ep = const.
Работа А, совершаемая результирующей силой, определяется как мера, изменения кинетической энергии материальной точки:
A = ∆EкT = Eк2 – Eк1.
Основное уравнение динамики вращательного движения относительно неподвижной оси z
Мz = Jze,
где Мz – результирующий момент внешних сил относительно оси z, действующих на тело; e – угловое ускорение; Jz – момент инерции относительно оси вращения.
Моменты инерции некоторых тел массой m:
а) стержня длиной l относительно оси, перпендикулярной стержню и проходящей через его центр масс,
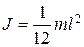 ;
;
б) обруча (тонкостенного цилиндра) относительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра) и проходящей через его центр масс,
J = mR2,
где R – радиус обруча (цилиндра);
в) диска радиусом R относительно оси, перпендикулярной плоскости диска и проходящей через его центр масс,
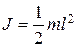 ;
;
г) тонкого круглого диска относительно оси, совпадающей с его диаметром
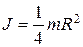 ,
,
где R – радиус диска.
д) шара относительно оси, проходящей через центр шара
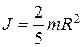
где R – радиус шара.
Проекция на ось z момента импульса тела, вращающегося относительно неподвижной оси z,
Lz = Jzω,
где ω – угловая скорость тела.
Закон сохранения момента импульса систем тел, вращающихся вокруг неподвижной оси z,
Jzω = const,
где Jz – момент инерции системы тел относительно оси z; ω – угловая скорость вращения тел системы вокруг оси z.
Кинетическая энергия тела, вращающегося вокруг неподвижной оси z,
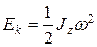 , или
, или 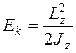 .
.
Релятивистская механика.Релятивистская масса
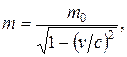 или
или 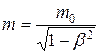 ,
,
где m0 – масса покоя частицы; v – ее скорость; c – скорость света в вакууме;b – скорость частицы, выраженная в долях скорости света ( 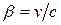 ).
).
Взаимосвязь массы и энергии релятивистской частицы
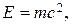 или
или 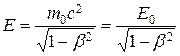 ,
,
где 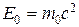 – энергия покоя частицы.
– энергия покоя частицы.
Полная энергия свободной частицы
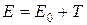 ,
,
где T – кинетическая энергия релятивистской частицы.
Кинетическая энергия релятивистской частицы
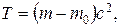 или
или 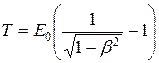 .
.
Импульс релятивистской частицы
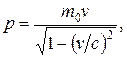 или
или 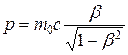 .
.
Связь между полной энергией и импульсом релятивистской частицы
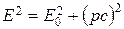 .
.
Молекулярная физика. Термодинамика.Количество вещества тела (системы)
v = N/Na,
где N - число структурных элементов (молекул атомов, ионов и т.п.), составляющих тело (систему); NA – постоянная Авогадро (Nа=6,02.1023 моль-1).
Молярная масса вещества
М = m/v,
где т – масса однородного тела (системы); v – количество вещества этого тела.
Относительная молекулярная масса вещества
Mr=ΣniAr,I,
где ni – число атомов i-гo химического элемента, входятих в состав молекулы данного вещества; Ar, t – относительная атомная масса этого элемента. Относительные атомные массы приводятся в таблице Д. И. Менделеева.
Связь молярной массы М с относительной молекулярной массой вещества
М = Mrk,
где k = 10-3 кг/моль.
Количество вещества смеси газов
v = v1 + v2 +…+ vn = N1/NA+N2/NA+…+Nn/NA,
или
v = 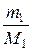 +
+ 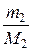 + … +
+ … + 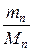 ,
,
где v1, N1, mi, Mi, – соответственно количество вещества, число молекул, масса, молярная масса i-го компонента смеси.
Уравнение Менделеева-Клапейрона (уравнение состояния идеального газа)
pV = 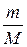 RT = vRT,
RT = vRT,
где т – масса газа, М – молярная масса газа, R – молярная газовая постоянная, v – количество вещества, Т – термодинамическая температура.
Опытные газовые законы, являющиеся частными случаями уравнения Менделеева-Клапейрона для изопроцессов:
а) закон Бойля-Мариотта (изотермический процесс: T = const, m = const)
pV = const
или для двух состояний газа
p1V1 = p2V2
б) закон Гей-Люссака (изобарный процесс: р = const, m = const)
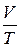 = const,
= const,
или для двух состояний
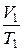 =
= 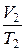 ;
;
в) закон Шарля (изохорный процесс: V = const, m = const)
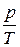 = const,
= const,
или для двух состояний
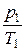 =
= 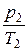 ;
;
г) объединенный газовый закон (m = const)
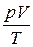 = const, или
= const, или 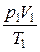 =
= 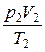 ,
,
где p1, V1, T1 – давление, объем и температура газа в начальном состоянии; р2, V2, T2 – те же величины в конечном состоянии.
Закон Дальтона, определяющий давление смеси газов,
р = p1 + p2 +…+ pn,
где pi – парциальные давления компонентов смеси; n – число компонентов смеси.
Парциальным давлением называется давление газа, которое производил бы этот газ, если бы только он один находился в сосуде, занятом смесью.
Молярная масса смеси газов
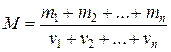 ,
,
где m – масса i-го компонента смеси; vi= 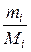 – количество вещества i-гo компонента смеси; n – число компонентов смеси.
– количество вещества i-гo компонента смеси; n – число компонентов смеси.
Массовая доля г-го компонента смеси газа (в долях единицы или процентах)
ωi = 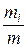 ,
,
где m – масса смеси.
Концентрация молекул
n = 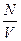 =
= 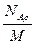
где N – число молекул, содержащихся в данной системе; ρ – плотность вещества; V – объем системы. Формула справедлива не только для газов, но и для любого агрегатного состояния вещества.
Основное уравнение кинетической теории газов
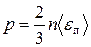 ,
,
где 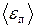 – средняя кинетическая энергия поступательного движения молекулы.
– средняя кинетическая энергия поступательного движения молекулы.
Средняя кинетическая энергия поступательного движения молекулы
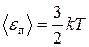 ,
,
где k – постоянная Больцмана.
Средняя полная кинетическая энергия
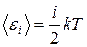 ,
,
где i – число степеней свободы молекулы
Зависимость давления газа от концентрации молекул и температуры
р = nkT.
Закон распределения молекул по скоростям (закон Максвелла): число молекул DN, относительные скорости которых лежат в интервале от u до u +Du, равно
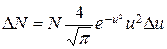
где N – полное число молекул газа, u = v/vв, где v – данная скорость, vв – наиболее вероятная скорость.
Скорости молекул:
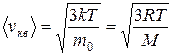 - средняя квадратичная;
- средняя квадратичная;
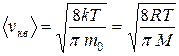 - средняя арифметическая;
- средняя арифметическая;
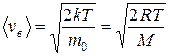 - наиболее вероятная,
- наиболее вероятная,
где m0– масса одной молекулы.
Относительная скорость молекулы
и = v/vB,
где v – скорость данной молекулы.
Среднее число столкновений одной молекулы за секунду
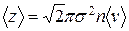 ,
,
где s - эффективный диаметр молекулы, n – концентрация молекул.
Удельные теплоемкости газа при постоянном объеме (сv) и постоянном давлении (сp)
Cv = 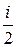
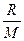 , Cр =
, Cр = 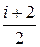
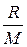 .
.
Связь между удельной с и молярной С теплоемкостями
с = С/М, С = сМ.
Уравнение Майера
Ср – Cv = R.
Внутренняя энергия идеального газа
U= 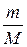
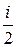 RT=
RT= 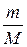 CVT.
CVT.
Первое начало термодинамики
Q = ∆U + A,
где Q – теплота, сообщенная системе (газу); ∆U – изменение внутренней энергии системы; А – работа, совершенная системой против внешних сил.
Работа расширения газа:
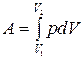 в общем случае;
в общем случае;
A = p(V2 – V1) при изобарном процессе;
A= 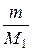 RTln
RTln 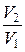 при изотермическом процессе;
при изотермическом процессе;
A = –∆U = – 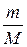 CV∆T, или A=
CV∆T, или A= 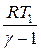
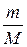
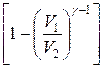
при изотермическом процессе; где γ=cp/cv–показатель адиабаты.
Уравнения Пуассона, связывающие параметры идеального газа при адиабатном процессе:
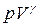 = const,
= const, 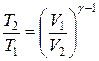 ,
,
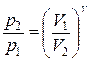 ,
, 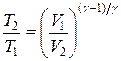
Термический КПД цикла
η = 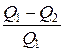 ,
,
где Q1 – теплота, полученная рабочим телом от теплоотдатчика; Q2 – теплота, переданная рабочим телом теплоприемнику.
Термический КПД цикла Карно
Η = 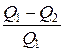 =
= 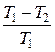 ,
,
где Т1и Т2 – термодинамические температуры теплоотдатчика и теплоприемника.
Изменение энтропии тела в любом обратимом процессе, переводящем его состояния A в состояние B
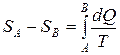 ,
,
где dQ – элементарное количество теплоты, полученное телом при температуре T.
Коэффициент поверхностного натяжения
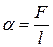 , или
, или 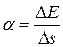 ,
,
где F – сила поверхностного натяжения, действующая на контур l, ограничивающий поверхность жидкости; DE – изменение свободной энергии поверхности пленки жидкости, связанное с изменением площади Ds поверхности этой пленки.
Формула Лапласа, выражающая давление p, создаваемое сферической поверхностью жидкости
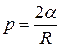 ,
,
где R – радиус сферической поверхности.
Высота подъема жидкости в капиллярной трубке
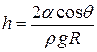 ,
,
где q – краевой угол (q = 0 при полном смачивании стенок трубки жидкостью; q = p при полном несмачивании); R – радиус канала трубки; r - плотность жидкости; g – ускорение свободного падения.
Высота подъема жидкости между двумя близкими параллельными друг другу плоскостями
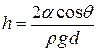 ,
,
где d – расстояние между плоскостями.
Электростатика. Постоянный электрический ток.Закон Кулона
F= 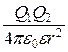 ,
,
где F – сила взаимодействия точечных зарядов Q1 и Q2; r – расстояние между зарядами; ε – диэлектрическая проницаемость; ε0 – электрическая постоянная.
Напряженность электрического поля и потенциал
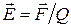 , φ = Ep/Q,
, φ = Ep/Q,
где Ep – потенциальная энергия точечного положительного заряда Q, находящегося в данной точке поля (при условии, что потенциальная энергия заряда, удаленного в бесконечность, равна нулю).
Сила, действующая на точечный заряд, находящийся в электрическом поле, и потенциальная энергия этого заряда
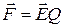 , Ep =Qj.
, Ep =Qj.
Напряженность и потенциал поля, создаваемого системой точечных зарядов (принцип суперпозиции электрических полей),
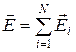 ,
, 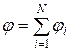
где 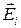 , ji – напряженность и потенциал в данной точке поля, создаваемого i-м зарядом.
, ji – напряженность и потенциал в данной точке поля, создаваемого i-м зарядом.
Напряженность и потенциал поля, создаваемого точечным зарядом
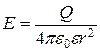 ,
, 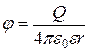
где r – расстояние от заряда Q до точки, в которой определяются напряженность и потенциал.
Напряженность и потенциал поля, создаваемого проводящей заряженной сферой радиусом R на расстоянии r от центра сферы:
а) Е = 0; 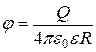 (при r < R);
(при r < R);
б) 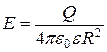 ;
; 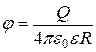 (при r = R);
(при r = R);
в) 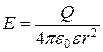 ;
; 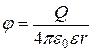 (при r>R);
(при r>R);
где Q – заряд сферы.
Линейная плотность заряда
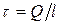 .
.
Поверхностная плотность заряда
σ = Q/S.
Напряженность и потенциал поля, создаваемого распределенными зарядами. Если заряд равномерно распределен вдоль линии с линейной плотностью t, то на линии выделяется малый участок длиной dl с зарядом dQ = t dl. Такой заряд можно рассматривать как точечный и применять формулы
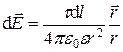 ;
; 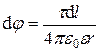 ,
,
где 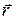 – радиус-вектор, направленный от выделенного элемента dl к точке, в которой вычисляется напряженность.
– радиус-вектор, направленный от выделенного элемента dl к точке, в которой вычисляется напряженность.
Используя принцип суперпозиции электрических полей, находим интегрированием напряженность 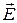 и потенциал φ поля, создаваемого распределенным зарядом:
и потенциал φ поля, создаваемого распределенным зарядом:
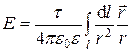 ;
; 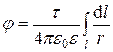 .
.
Интегрирование ведется вдоль всей длины l заряженной линии.
Напряженность поля, создаваемого бесконечной прямой равномерно заряженной линией или бесконечно длинным цилиндром
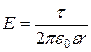 ,
,
где r – расстояние от нити или оси цилиндра до точки, напряженность поля в которой определяется.
Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью
Е= 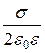 .
.
Связь потенциала с напряженностью:
a) 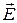 = -gradφ, или
= -gradφ, или 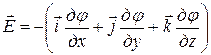 в общем случае;
в общем случае;
б) 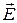 = (j1 – j2)/d в случае однородного поля;
= (j1 – j2)/d в случае однородного поля;
в) 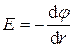 в случае поля, обладающего центральной или осевой симметрией.
в случае поля, обладающего центральной или осевой симметрией.
Электрический момент диполя
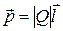 ,
,
где Q – заряд; 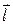 – плечо диполя (векторная величина, направленная от отрицательного заряда к положительному и численно равная расстоянию между зарядами).
– плечо диполя (векторная величина, направленная от отрицательного заряда к положительному и численно равная расстоянию между зарядами).
Работа сил поля по перемещению заряда Q из точки поля с потенциалом j1 в точку с потенциалом j2.
A12 = Q(j1 – j2)
или
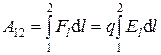 ,
,
где El – проекция вектора напряженности на направление dl.
Электроемкость
C = Q/j, или C = Q/U
где j – потенциал проводника (при условии, что в бесконечности потенциал проводника принимается равным нулю); U – разность потенциалов пластин конденсатора.
Электроемкость плоского конденсатора
С = ε0εS/d
где S – площадь пластины (одной) конденсатора; d – расстояние между пластинами.
Электроемкость батареи конденсаторов:
а) 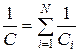 при последовательном соединении;
при последовательном соединении;
б) 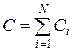 при параллельном соединении,
при параллельном соединении,
где N – число конденсаторов в батарее.
Энергия заряженного конденсатора:
W = QU/2, W = CU2/2, W = Q2/(2C).
Сила постоянного тока
I = Q/t,
где Q – заряд, прошедший через поперечное сечение проводника за время t.
Плотность тока
J = I/S,
где S – площадь поперечного сечения проводника.
Связь плотности тока со средней скоростью <v> направленного движения заряженных частиц
J = Qn<v>,
где Q – заряд частицы; n – концентрация заряженных частиц.
Закон Ома:
a) 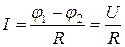 для участка цепи, не содержащего ЭДС, где j1 – j2 = U – разность потенциалов (напряжение) на концах участка цепи; R – сопротивление участка;
для участка цепи, не содержащего ЭДС, где j1 – j2 = U – разность потенциалов (напряжение) на концах участка цепи; R – сопротивление участка;
б) 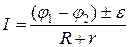 для участка цепи, содержащего ЭДС, где e – ЭДС источника тока; R – полное coпротивление участка; r – внутреннее coпротивленее источника;
для участка цепи, содержащего ЭДС, где e – ЭДС источника тока; R – полное coпротивление участка; r – внутреннее coпротивленее источника;
в) 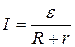 для замкнутой (полной) цепи, где R – внешнее сопротивление цепи; r – внутреннее сопротивление цепи.
для замкнутой (полной) цепи, где R – внешнее сопротивление цепи; r – внутреннее сопротивление цепи.
Законы Кирхгофа:
а) ΣIi = 0 – первый закон;
б) ΣIiRi = Σei – второй закон,
где ΣIi – алгебраическая сумма сил токов, сходящихся в узле; ΣIiRi – алгебраическая сумма произведений сил токов на сопротивления участков; ΣeI – алгебраическая сумма ЭДС.
Сопротивление R и проводимость G проводника
R = ρl/S, G = γS/l,
где ρ – удельное сопротивление; γ – удельная проводимость; l – длина проводника; S – площадь поперечного сечения проводника.
Сопротивление системы проводников:
а) R = ΣR при последовательном соединении;
б) 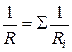 при параллельном соединении, где Ri – сопротивление i-гo проводника.
при параллельном соединении, где Ri – сопротивление i-гo проводника.
Работа тока:
А = IUt, A = I2Rt, A = U2t/R.
Первая формула справедлива для любого участка цепи, на концах которого поддерживается напряжение U, последние две – для участка, не содержащего ЭДС.
Мощность тока:
P = IU, P = I2R, Р = U2/R.
Закон Джоуля–Ленца
Q = I2Rt.
Закон Ома в дифференциальной форме
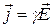 ,
,
где γ – удельная проводимость; 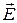 – напряженность электрического поля;
– напряженность электрического поля; 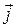 – плотность тока.
– плотность тока.
Связь удельной проводимости γ с подвижностью b заряженных частиц (ионов)
γ = Qn(b+ + b–),
где Q – заряд иона; n – концентрация ионов; b+ и b– – подвижности положительных и отрицательных ионов.
Электромагнетизм.Связь магнитной индукции 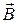 с напряженностью
с напряженностью 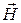 магнитного поля
магнитного поля
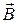 = μμ0
= μμ0 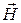
где μ – магнитная проницаемость изотропной среды; μ0 – магнитная постоянная. В вакууме μ = 1, и тогда магнитная индукция в вакууме
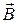 =μ0
=μ0 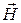
Закон Био–Савара–Лапласа
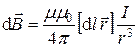 или
или 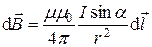 ,
,
где 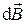 – магнитная индукция поля, создаваемого элементом провода длиной dl с током I;
– магнитная индукция поля, создаваемого элементом провода длиной dl с током I; 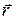 – радиус-вектор, направленный от элемента проводника к точке, в которой определяется магнитная индукция; a – угол между радиусом-вектором и направлением тока в элементе провода.
– радиус-вектор, направленный от элемента проводника к точке, в которой определяется магнитная индукция; a – угол между радиусом-вектором и направлением тока в элементе провода.
Магнитная индукция в центре кругового тока
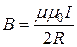 ,
,
где R – радиус кругового витка.
Магнитная индукция на оси кругового тока
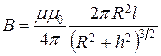 ,
,
где h – расстояние от центра витка до точки, в которой определяется магнитная индукция.
Магнитная индукция поля прямого тока.
В = μμ0I/(2πr0),
где r0 – расстояние от оси провода до точки, в которой определяется магнитная индукция.
Магнитная индукция поля, создаваемого отрезком провода с током,
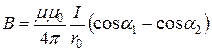 .
.
Магнитная индукция поля соленоида
В = μμ0nI,
где n – отношение числа витков соленоида к его длине.
Сила, действующая на провод с током в магнитном поле (закон Ампера),
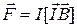 , или F = IBlsinα,
, или F = IBlsinα,
где I – длина провода; a – угол между направлением тока в проводе и вектором магнитной индукции 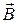 . Это выражение справедливо для однородного магнитного поля и прямого отрезка провода. Если поле неоднородно и провод не является прямым, то закон Ампера можно применять к каждому элементу провода в отдельности:
. Это выражение справедливо для однородного магнитного поля и прямого отрезка провода. Если поле неоднородно и провод не является прямым, то закон Ампера можно применять к каждому элементу провода в отдельности:
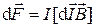 .
.
Магнитный момент плоского контура с током
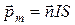 ,
,
где 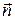 – единичный вектор нормали (положительной) к плоскости контура; I – сила тока, протекающего по контуру; S – площадь контура.
– единичный вектор нормали (положительной) к плоскости контура; I – сила тока, протекающего по контуру; S – площадь контура.
Механический (вращательный) момент, действующий на контур с током, помещенный в однородное магнитное поле,
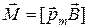 , или M = pmВsina,
, или M = pmВsina,
где a – угол между векторами 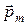 и
и 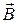 .
.
Потенциальная энергия (механическая) контура с контура с током в магнитном поле
Ep,мех = – 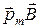 , или Ep,мех = –pmВcosa
, или Ep,мех = –pmВcosa
Отношение магнитного момента pm к механическому L (моменту импульса) заряженной частицы, движущейся по крутой орбите,
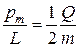 ,
,
где Q – заряд частицы; m – масса частицы.
Сила Лоренца
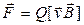 , или F = QvBsina,
, или F = QvBsina,
где 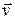 – скорость заряженной частицы; a – угол между векторами
– скорость заряженной частицы; a – угол между векторами 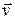 и
и 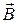 .
.
Магнитный поток:
а) в случае однородного магнитного поля и плоской поверхности
Ф = BScosa или Ф = BnS,
где S – площадь контура; a – угол между нормалью к плоскости контура и вектором магнитной индукции:
б) в случае неоднородного поля и произвольной поверхности
Ф = 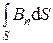 .
.
(интегрирование ведется по всей поверхности).
Потокосцепление (полный поток)
Y = NФ.
Эта формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу N витков.
Работа по перемещению замкнутого контура в магнитном поле
A = I∆Ф
ЭДС индукции
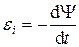 .
.
Разность потенциалов на концах провода, движущегося со скоростью 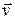 в магнитном поле,
в магнитном поле,
U = Blvsina,
где l – длина провода; a – угол между векторами 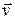 и
и 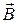 .
.
Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего этот контур,
Q = ∆Ф/R, или Q = N∆Ф/R = ∆Y/R,
где R – сопротивление контура.
Индуктивность контура
L = Ф/I.
ЭДС самоиндукции
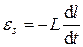 .
.
Индуктивность соленоида
L = μμ0n2V,
где п – отношение числа витков соленоида к его длине; V – объем соленоида.
Мгновенное значение силы тока в цепи, обладающей сопротивлением R и индуктивностью L:
а) 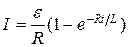 (при замыкании цепи), где e – ЭДС источника тока; t – время, прошедшее после замыкания цепи;
(при замыкании цепи), где e – ЭДС источника тока; t – время, прошедшее после замыкания цепи;
б) 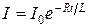 (при размыкании цепи), где l0 – сила тока в цепи при t = 0; t – время, прошедшее с момента размыкания цепи.
(при размыкании цепи), где l0 – сила тока в цепи при t = 0; t – время, прошедшее с момента размыкания цепи.
Энергия магнитного поля
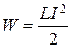 .
.
Объемная плотность энергии магнитного поля (отношение энергии магнитного поля соленоида к его объему)
w = BH/2, или w = В2/(2μμ0), или w = μμ0H 2/2
где В – магнитная индукция; H – напряженность магнитного поля.
Волновая оптика.Скорость света в среде
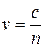 ,
,
где с – скорость света в вакууме; n – показатель преломления среды.
Оптическая длина пути световой волны
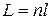 ,
,
где l – геометрическая длина пути световой волны в среде с показателем преломления n.
Оптическая разность хода двух световых волн
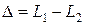 .
.
Зависимость разности фаз оптической разности хода световых вол
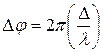 ,
,
где l – длина световой волны.
Условие максимального усиления света при интерференции
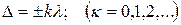
Условие максимального ослабления света
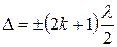 .
.
Оптическая разность хода световых волн, возникающая при отражении монохроматического света от тонкой пленки,
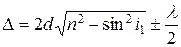 , или
, или 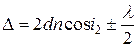 ,
,
где d – толщина пленки, n – показатель преломления пленки; i1 – угол падения; i2– преломления света в пленке.
Радиус светлых колец Ньютона в отраженном свете
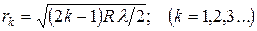
где k – номер кольца; R – радиус кривизны.
Радиус темных колец Ньютона в отраженном свете
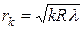 .
.
Угол j отклонения лучей, соответствующий максимуму (светлая полоса) при дифракции на одной щели, определяется из условия
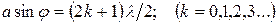 ,
,
где a – ширина щели; k – порядковый номер максимума.
Угол j отклонения лучей, соответствующий максимуму (светлая полоса) при дифракции света на дифракционной решетке, определяется из условия
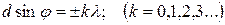
где d – период дифракционной решетки.
Разрешающая способность дифракционной решетки
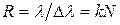 ,
,
где Dl – наименьшая разность длин волн двух соседних спектральных линий (l и l + Dl),при которой эти линии могут быть видны раздельно в спектре, полученным посредством данной решетки; N – полное число щелей решетки.
Формула Вульфа–Брэгга
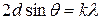 ,
,
где q – угол скольжения (угол между направлением параллельного пучка рентгеновского излучения, падающего на кристалл, и атомной плоскостью в кристалле); d – расстояние между атомными плоскостями кристалла.
Закон Брюстера
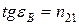 ,
,
где 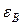 – угол падения, при котором отразившийся от диэлектрика луч полностью поляризован;
– угол падения, при котором отразившийся от диэлектрика луч полностью поляризован; 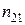 – относительный показатель преломления второй среды относительно первой.
– относительный показатель преломления второй среды относительно первой.
Закон Малюса
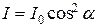
где I0 – интенсивность плоскополяризованного света, падающего на анализатор; I – интенсивность этого света после анализатора; a – угол между направлением колебаний электрического вектора света, падающего на анализатор, и плоскостью пропускания анализатора (если колебания электрического вектора падающего света совпадают с этой плоскостью, то анализатор пропускает данный свет без ослабления).
Угол поворота плоскости поляризации монохроматического света при прохождении через оптически активное вещество:
а) j = ad (в твердых телах),
где a – постоянная вращения, d – длина пути, пройденная светом в оптически активном веществе;
б) j = [a]rd (в растворах),
где [a] – удельное вращение; r – массовая концентрация оптически активного вещества в растворе.
Тепловое излучение.Закон Стефана–Больцмана для абсолютно черного тела
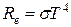 ,
,
где Re –энергетическая светимость (излучательность) абсолютно черного тела; s – постоянная Стефана–Больцмана; T – термодинамическая температура Кельвина.
Закон Стефана–Больцмана для нечерных тел
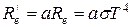 ,
,
где a – коэффициент излучения, показывающий, какую часть составляет энергетическая светимость 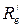 данного тела от энергетической светимости Re абсолютно черного тела, взятого при той же температур.
данного тела от энергетической светимости Re абсолютно черного тела, взятого при той же температур.
Связь между радиационной температурой Tp тела и его истинной температурой T
 .
.
Закон смещения Вина
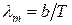 ,
,
где lm – длина волны, на которую приходится максимальная энергия излучения; b – постоянная Вина.
Формула Планка для спектральной плотности энергетической светимости абсолютно черного тела
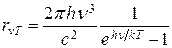
где h – постоянная планка, k – постоянная Больцмана, c – скорость света, n - частота излучения.
Квантовая природа света.Энергия фотона
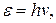 или
или 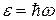 ,
,
где h – постоянная Планка; 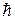 – постоянная Планка, деленная на 2p; n – частота фотона; w – циклическая частота.
– постоянная Планка, деленная на 2p; n – частота фотона; w – циклическая частота.
Масса фотона
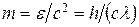 ,
,
где c – скорость света в вакууме; l – длина волны фотона.
Импульс фотона
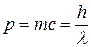 .
.
Формула Эйнштейна для фотоэффекта
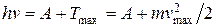 ,
,
где hn – энергия фотона, падающая на поверхность металла; A – работа выхода электрона; Tmax – максимальная кинетическая энергия фотоэффекта
Красная граница фотоэффекта
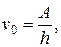 или
или 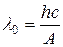 ,
,
где n0 – минимальная частота света, при которой еще возможен фотоэффект; l0 – максимальная длина волны света, при которой еще возможен фотоэффект; h – постоянная Планка; c – скорость света в вакууме.
Формула Комптона
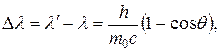 или
или 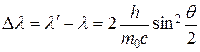 ,
,
где l – длина волны фотона, встретившегося со свободным или слабосвязанным электроном; l/ – длина волны фотона, рассеянного на угол q после столкновения с электроном; m0 – масса покоящегося электрона.
Комптоновская длина волны
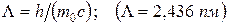 .
.
Давление света при нормальном падении на поверхность
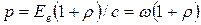 ,
,
где Ee – энергетическая освещенность (облученность); r – коэффициент отражения; w – объемная плоскость энергии излучения.
Атом Бора.Момент импульса электрона (второй постулат Бора)
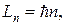 или
или 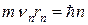 ,
,
где m – масса электрона; vn – скорость электрона на n-ой орбите; rn–радиус n-ой стационарной орбиты; 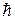 –постоянная Плана; n – главное квантовое число (n = 1,2,3,…).
–постоянная Плана; n – главное квантовое число (n = 1,2,3,…).
Радиус n-ой стационарной орбиты
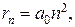
где a0 – первый боровский радиус.
Энергия электрона в атоме водорода
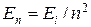 ,
,
где Ei – энергия ионизации атома водорода.
Энергия, излучаемая или поглощаемая атомом водорода,
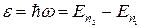 , или
, или 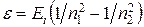 ,
,
где n1 и n2 – квантовые числа, соответствующие энергетическим уравнениям, между которыми совершается переход электрона в атоме.
Спектроскопическое волновое число
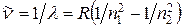 ,
,
где l – длина волны излучения или поглощения атомом; R – постоянная Ридберга.
Элементы квантовой механики.Длина волны де Бройля
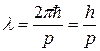 ,
,
где p – импульс частицы.
Импульс частицы и его связь с кинетической энергией 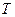 :
:
а) 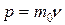 ;
; 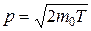 ;
;
б) 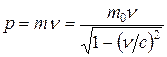 ;
; 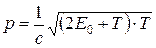 ,
,
где m0 – масса покоя частицы; m – релятивистская масса; v – скорость частицы; c – скорость света в вакууме; E0 – энергия покоя частицы.
Соотношение неопределённостей Гейзенберга:
а) 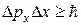 (для координаты и импульса),
(для координаты и импульса),
где 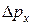 – неопределенность проекции импульса на ось X; Dx – неопределенность координаты;
– неопределенность проекции импульса на ось X; Dx – неопределенность координаты;
б) 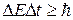 (для энергии и времени),
(для энергии и времени),
где DE – неопределенность энергии; Dt – время жизни квантовой системы в данном энергетическом состоянии.
Одномерное уравнение Шредингера для стационарных состояний
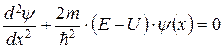 ,
,
где 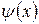 – волновая функция, описывающая состояние частицы; m – масса частицы; E – полная энергия; U = U(x) – потенциальная энергия частицы.
– волновая функция, описывающая состояние частицы; m – масса частицы; E – полная энергия; U = U(x) – потенциальная энергия частицы.
Плотность вероятности
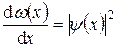 ,
,
где dw(x) – вероятность того, что частица может быть обнаружена вблизи точки с координатой x на участке dx.
Вероятность обнаружения частицы в интервале от 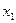 до
до 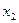
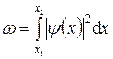 .
.
Решение уравнения Шредингера для одномерного, бесконечно глубокого, прямоугольного потенциального ящика:
а) 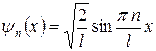 (собственная нормированная волновая функция);
(собственная нормированная волновая функция);
б) 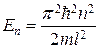 (собственное значение энергии),
(собственное значение энергии),
