Элементы квантовой статистики
Квантовая статистика.
Фазовое пространство.
Функция распределения
Квантовая статистика — раздел статистической физики, исследующий системы, которые состоят из огромного числа частиц, подчиняющихся законам квантовой механики.
В отличие от исходных положений классической статистической физики, в которой тождественные частицы различимы (частицу можно отличить от всех таких же частиц), квантовая статистика основывается на принципе неразличимости тождественных частиц (см. § 226). При этом оказывается, как будет показано ниже, что коллективы частиц с целым и полуцелым спинами подчиняются разным статистикам.
Пусть система состоит из N частиц. Введем в рассмотрение многомерное пространство всех координат и импульсов частиц системы. Тогда состояние системы определяется заданием 6N переменных, так как состояние каждой частицы определяется трой кой координат х, у, z и тройкой соответствующих проекций импульса рх, ру, рz.Соответственно число «взаимно перпендикулярных» координатных осей данного про странства равно 6N. Это 6N-мерное пространство называется фазовым пространством. Каждому микросостоянию системы отвечает точка в 6N-мерном фазовом пространстве, так как задание точки фазового пространства означает задание координат и им пульсов всех частиц системы. Разобьем фазовое пространство на малые 6N-мерные элементарные ячейки объемом dqdp = dq1dq2 … dq3Ndp1dp2...dp3N, где q— совокупность координат всех частиц, р— совокупность проекций их импульсов. Корпускуляр-но-волновой дуализм свойств вещества (см. § 213) и соотношение неопределенностей Гейзенберга (см. § 215) приводят к выводу, что объем элементарной ячейки (он называется фазовым объемом) не может быть меньше чем h3 (h— постоянная Планка).
Вероятность dW данного состояния системы можно представить с помощью функции распределения f(q, p):
dW = f(q,p) dq dp. (234.1)
Здесь dW—вероятность того, что точка фазового пространства попадет в элемент фазового объема dqdp, расположенного вблизи данной точки q, р. Иными словами, dW представляет собой вероятность того, что система находится в состоянии, в котором ее координаты и импульсы заключены в интервале q, q+dq и р, p+dp.
Согласно формуле (234.1), функция распределения есть не что иное, как плотность вероятности определенного состояния системы. Поэтому она должна быть нормирована на единицу:
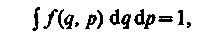
где интегрирование производится по всему фазовому пространству.
Зная функцию распределения f(q, p) , можно решить основную задачу квантовой статистики — определить средние значения величин, характеризующих рассматрива емую систему. Среднее значение любой функции
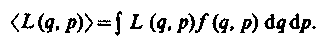 (234.2)
(234.2)
Если иметь дело не с координатами и импульсами, а с энергией, которая квантуется, то состояние системы характеризуется не непрерывной, а дискретной функцией распределения.
Явное выражение функции распределения в самом общем виде получил американский физик Д. Гиббс (1839—1903). Оно называется каноническим распределением Гиббса. В квантовой статистике каноническое распределение Гиббса имеет вид
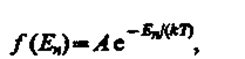 (234.3)
(234.3)
где А — постоянная, определяемая из условия нормировки к единице, n— совокупность всех квантовых чисел, характеризующих данное состояние. Подчеркнем, что f(En)есть именно вероятность данного состояния, а не вероятность того, что система имеет определенное значение энергии Еn,так как данной энергии может соответствовать не одно, а несколько различных состояний (может иметь место вырождение).
