Изобарлы процестің жұмысы
l= 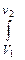 pdV=P(V2-V1)=R(T2-T1) (1.4.7)
pdV=P(V2-V1)=R(T2-T1) (1.4.7)
Газды қыздыруға келтірілген (немесе ол салқындағанда алынатын) жылуың мөлшелерін термодинамиканың бірінші заңынан анықтауға болады dq=dh-VdP=idem
q=h2-h1=Δh= 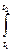
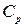 dT=
dT= 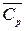
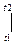 (t2-t1). (1.4.8)
(t2-t1). (1.4.8)
Мұндағы 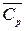
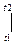 - t1-ден t2-ге дейінгі температуралар аралығындағы орта массалық изобарлық жылу сыйымдылық, мұнда Cp=idem
- t1-ден t2-ге дейінгі температуралар аралығындағы орта массалық изобарлық жылу сыйымдылық, мұнда Cp=idem
q=Cp(t2- t1)=Δh (1.4.9)
Изотермиялық процесс
Бұл процесте температура турақты, соның үшін
PV=RT=const, немесе
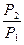 =
= 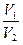 . (1.4.10)
. (1.4.10)
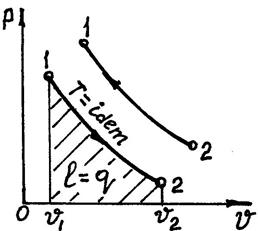
Яғни газдың қысымы оның көлеміне кері пропорционал болады, сондықтан газ изотермиялық қысылғанда қысымы үлкейді, ал газ изотермиялық ұлғайса, қысымы кішірейеді (Бойль-Мариотт заңы)
(1.4.10) – байланысты, бұл процестің графигі Р, V – координаттарында тең бүйірлі гипербола болады. (1.11-сурет)
1.11-сурет
Процестің жұмысы
l= 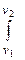 РdV=
РdV= 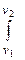 RTdV/V=RTln(V2/V1)= RTln(
RTdV/V=RTln(V2/V1)= RTln( 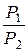 ); (1.4.11)
); (1.4.11)
Температура өзгермеуеіне байланысты иделды газдың ішкі энергиясы бұл процесте тұрақты болады ΔU=0 және Δh=0, сондықтан барлық газға келтірілген жылулық толық жұмысқа айналады:
q=1. (1.4.12)
Gт=dq/dт – жылу сыйымдылық формуласы көрсететіндей, изотермиялық процесте газдың жылусыйымдылығы ∞ тең.
Адиабаталық процесс.
Бұл процесс жүргізілгенде қоршаған ортамен жылу алмасу болмайды, осыған байланысты δq=0
Адиабаталық процесс үшін термодинамиканың бірінші заңы мынадай түрде жазылады
PVк=idem, (1.4.13)
мұндағы к=Ср/СV – адиабаталық көрсеткіш.
Адиабатылық процестің графигі (1.12-суретте) көрсетілген.
Адиабата көрсеткіші к >1 болғандықтан адиабата изотермаға қарағанда құламалау келеді, өйткені адиабаталық ұлғайланғанда газдың температурасының төмендеуіне байланысты изотермалық процеске қарағанда қысым жылдамырақ төмендейді.
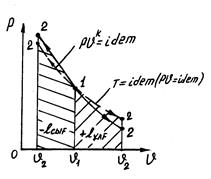
1.12-сурет
(1.4.13) теңдеуінен мынаны табамыз: Р1/Р2 =(V2/V1)к немесеV2/V1=(Р1/Р2)1/к (1.4.14)
(1.4.13) теңдеуі V, P координатындағы адиабаттық идеалды газдың теңдеуі Сv=idem және Ср= idem болғанда.
PV=RT күй теңдеуіне сәйкес, адибаттық процестегі тепмператураның көлемен немесе қысыммен байланысын көрсететін теңдеулерін табамыз:
ТVк-1=const, (1.4.15)
немесе Т1/Т2=(V2/V1)к-1 немесе(V2/V1)1/к-1 (1.4.16)
Т1/Т2=(Р1/Р2)к-1/к =(V2/V1)к-1 (1.4.17)
Бір атомды газ үшін к=1.66, екі атомды газ үшін к=1.4, ал үш және көп атомды газдар үшін к=1.33
Термодинамиканың бірінші заңы бойынша адиабатты процестегі ұлғаю жұмысы ішкі энергияның азаюымен жүреді және де төмендегі теңдеулердің біреуімен анықталады:
l= -∆U=CV(Т2-Т1)= 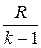 (Т1-Т2)=
(Т1-Т2)= 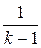 (Р1V1-P2V2)=
(Р1V1-P2V2)= 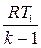 (1-
(1- 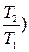 ) =
) =
= 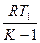 [1-(
[1-( 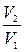 )k-1]=
)k-1]= 
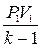 (1-
(1- 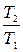 )=
)= 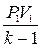 [1-(
[1-( 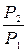 )
) 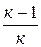 ] (1.4.18)
] (1.4.18)
Бұл процесте газдың қоршаған ортамен жылу алмасуы өзгермейді, сондықтан q=0, онда С=dq/dТ теңдеуінде, адиабаттық процестің жылусыйымдылығы нольге тең болады.(Сq=0).
Политроптық процесс
Политроптық процесс деп – жүйенің физикалық күйінің өзгеруінде газдың жылу- сыйымдылығы тұрақты сақталатын термодинамикалық процесті айтады. Егер барлық термодинамикалық процестер турақты жылусыйымдылықта өтетін болса, онда олар жеке кездейсоқ политропты процесс болады.
Политропты прцесс түсініктемелері, көбінесе жылу және газды двигательдердің, компрессолардың сығылу және улғаю жұмыстық процестерін оқып үйренуде қолданылады.
Кезкелген еркін процесті Р, V координатында (кіші учаскелі) төмендегі теңдікпен анықтайды.
Р Vn=idem, (1.4.19)
n – политроп көрсеткіші. Оның сандық мәні - ∞ пен + ∞ аралығында болуы мүмкін, бірақ көрсетілген процесс үшін ол тұрақты шама болады.
Политроп теңдеуі 1.4.19 адиабаттық теңдеуден айырмашылығы n-көрсеткіші, сондықтан барлық қатыныстағы негізгі параметрлерін адиабаттық процесіндегі формулаларымен анықтауға болады (1.4.14)-(1.4.18), бірақ адиабат көрсеткіштерінің К орнына политроп көрсеткіштерін n-ді қабылдау керек.
Политроп көрсеткіші n және полтироп процесінің жылусыйымдылығы Сn төмендегіше анықталады;
n= 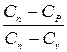 , (1.4.20)
, (1.4.20)
осыдан Сn=Cv* 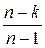 (1.4.21)
(1.4.21)
