Приложение В – Примеры определения импульсной передаточной функции

При определении импульсной передаточной функции импульсную систему представляют в виде структурной схемы, приведенной на рисунке В1.

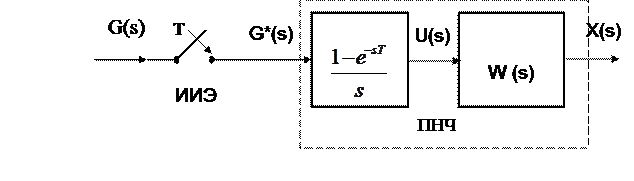
Рисунок В1 – Разомкнутая импульсная система

Пример В1. Определить импульсную передаточную функцию системы (рисунок В1) с формирующим элементом типа фиксатора нулевого порядка и непрерывной частью с передаточной функцией .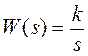

Решение

1) Передаточная функция ПНЧ:

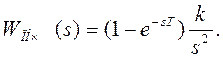
2) Вспомогательная передаточная функция W₁(s)=k/s².

3) Весовая функция ω₁(t) представляет обратное преобразование Лапласа от W₁(s), т.е.

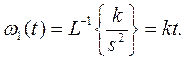
4) Решетчатая функция .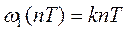

5) Передаточная функция W₁(s) в z-форме

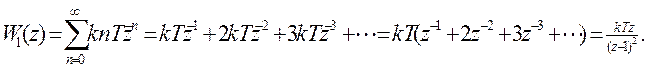
6) Z – преобразование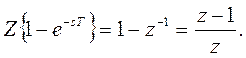

7) Окончательно имеем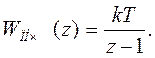

Пример В2. Определить импульсную передаточную функцию системы (рисунок В1) с формирующим элементом типа фиксатора нулевого порядка и непрерывной частью с передаточной функцией .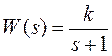

Решение

1) Передаточная функция ПНЧ:

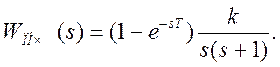
2) Вспомогательная передаточная функция

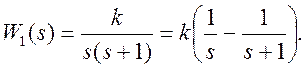
3) Весовая функция ω₁(t) представляет обратное преобразование Лапласа от W₁(s), т.е.

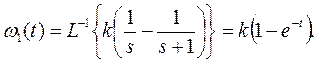
4) Решетчатая функция .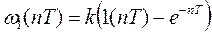

5) Передаточная функция W₁(s) в z-форме

.

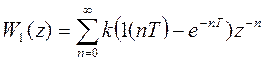6) Импульсная передаточная функция .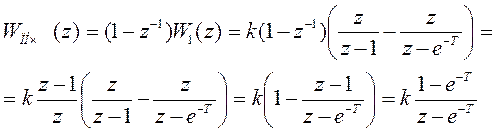

Приложение Г – Расчет и построение переходной характеристики импульсной системы

Пример Г. Передаточная функция непрерывной части импульсной системы (рисунок В1) .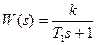

Требуется: 1)определить и построить переходную характеристику системы при условии: k=1, T₁=1 c, период квантования по времени Т=1c;

2) построить переходную характеристику при Т=0,1с;

3) поострить переходную характеристику, если в системе отсутствует импульсная часть, т.е. для непрерывной системы.

Решение

Согласно определению переходной функции необходимо получить выражение, определяющее реакцию системы на единичное ступенчатое воздействие, т.е. сигнал на входе системы g(t) =1(t).

1) Изображение по Лапласу сигнала на выходе

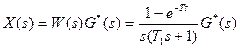(Г1)

2) Z-изображение сигнала на выходе x(t)

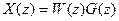(Г2)

3) Импульсная передаточная функция (см. пример В2)

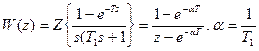. (Г3)

4) Изображение G(z) найдем из таблицы z-преобразований (приложение А)

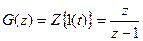. (Г4)

5) Учитывая (3) и (4) запишем z-изображение x(t)

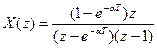. (Г5)

6) Импульсную переходную функцию x(nT) находим с помощью обратного z-преобразования. При этом, чтобы воспользоваться таблицей z-преобразований, необходимо выражение (Г5) разложить на простые дроби. Как видно из таблицы z-преобразований, числитель всех z-преобразований содержит множитель z. Поэтому на простые дроби раскладывается функция X(z)/ z , а затем каждая дробь умножается на z, чтобы придать разложению надлежащую форму.

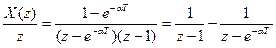; (Г6)

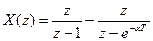. (Г7)

7) Следовательно,

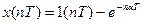. (Г8)

8) Подставляя в (Г8) n=0,1,2,…, вычисляем значения x(nT) и строим графики переходных характеристик

x(t)

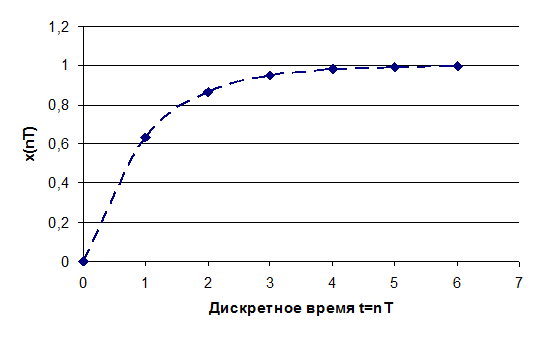
Рисунок Г1- Переходная функция импульсной системы Т=1 с и непрерывной системы (пунктирная линия)

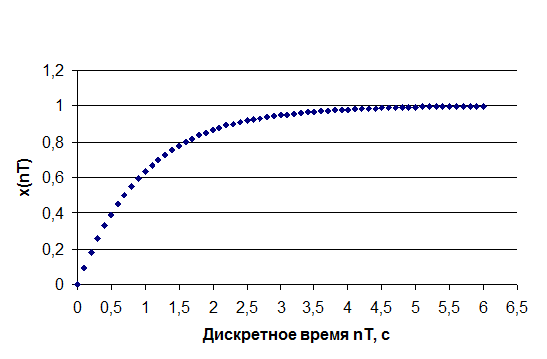
Рисунок Г2 - Переходная функция импульсной системы Т=0,1 с

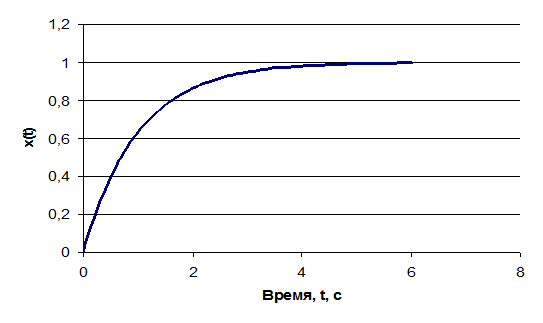
Рисунок Г2 - Переходная функция непрерывной системы

Как видно из графиков, в непрерывной системе переходная характеристика представляет собой экспоненту, Импульсная переходная характеристика соответствует непрерывной только в моменты квантования. Z- преобразование позволяет получить реакцию системы только в моменты квантования. Чем меньше период квантования, тем выше соответствие.