Абсолютно черное тело. Серое тело. Закон Кирхгофа.

По определению 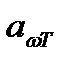не может быть больше единицы. Для тела, полностью поглощающего падающее на него излучение всех частот, 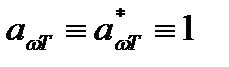. Такое тело называют абсолютно черным. Тело, для которого 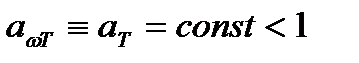, называется серым. Между испускательной и поглощательной способностью любого тела имеется определенная связь.

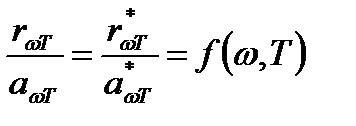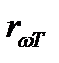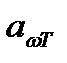Закон Кирхгофа: Отношение испускательной и поглощательной способностей не зависит от природы тела, оно является для всех тел одной и той же (универсальной) функцией частоты (длины волны) и температуры: .Сами величины и , взятые отдельно, могут меняться чрезвычайно сильно при переходе от одного тела к другому. Отношение же их оказывается одинаковым для всех тел. Это означает, что тело, сильнее поглощающее какие либо лучи, будет эти лучи сильнее и испускать.Для абсолютно черного тела по определению 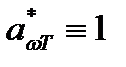. Следовательно, 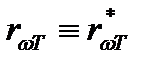для такого тела равна 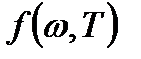. Таким образом, универсальная функция Кирхгофа 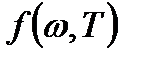есть не что иное, как испускательная способность абсолютно черного тела: 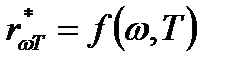.При теоретических исследованиях для характеристики спектрального состава равновесного теплового излучения удобнее пользоваться функцией частоты − 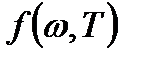. В экспериментальных работах удобнее пользоваться функцией длины волны − 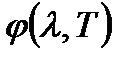. Обе функции связаны друг с другом формулой: 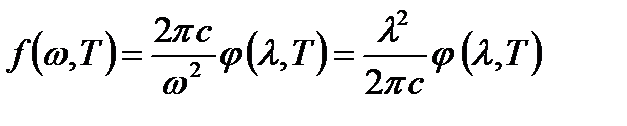.Для того, чтобы по известной функци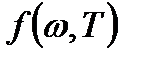и найти 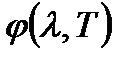, нужно заменить в 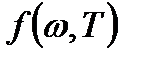частоту 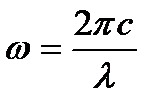и получившееся выражение умножить на 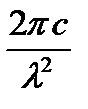: 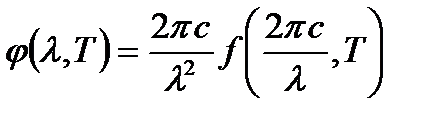.Для нахождения 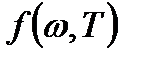по известной 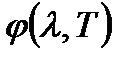нужно воспользоваться соотношением: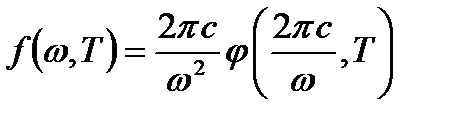

3. Равновесное излучение и его свойства. Спектральная плотность энергии излучения.Рассмотрим излучение, находящееся в равновесии с веществом. В равновесном состоянии энергия излучения будет распределена с определенной объемной плотностью 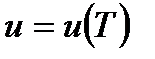. Спектральное распределение этой энергии можно охарактеризовать функцией 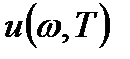, определяемой условием 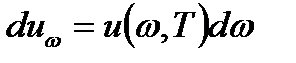, где 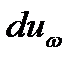− объемная плотность энергии излучения, приходящаяся на интервал частот 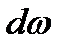. Полная плотность энергии 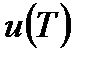связана с функцией 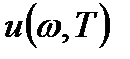формулой: 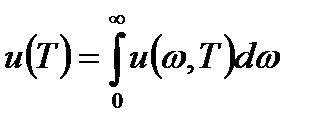. Равновесная плотность энергии теплового излучения 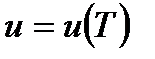связана с энергетической светимостью абсолютно черного тела 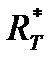и испускательной способностью абсолютно черного тела соотношениями: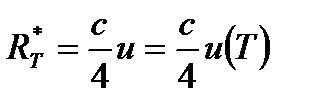 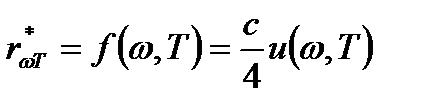, где − скорость света в вакууме. Св-ва РИ: 1)РИ однородно, изотропно, неполяризованное. 2)Т.к. излуч.нах.с ТД в равнов. со стенками полости, то им.смысл говорить не только о Т стенок, но и о Т РИ. Т_РИ-это св-во самого излучения и о ней есть смысл говорить, даже когда нет стенок. 3)из ТДих соображений след., что ОПэн. И РИ завис.только от Т и не завис. От материала и формы стенок полости. 4) Ри при Т тождественно изл. АЧТ при той же Т.Поэтому наз. черным излуч.

4. Закон Стефана-Больцмана. Формула Вина и закон смещения Вина. Формула Рэлея-Джинса.Из закона Кирхгофа следует, что испускательная способность абсолютно черного тела является универсальной функцией, поэтому нахождение ее явной зависимости от частоты 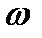и температуры 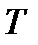является важной задачей теории теплового излучения. Австрийский физик Й. Стефан, анализируя экспериментальные данные, и Л. Больцман, применяя термодинамический метод, установили зависимость энергетической светимости абсолютно черного тела 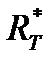от его абсолютной температуры. Закон Стефана-Больцмана: 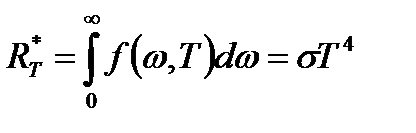, т.е. энергетическая светимость абсолютно черного тела пропорциональна четвертой степени его абсолютной температуры; где 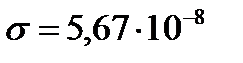Вт/(м²∙К⁴) − постоянная Стефана-Больцмана, 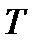− абсолютная температура абсолютно черного тела. Закон Стефана-Больцмана, определяя зависимость 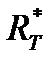от температуры, не дает ответа относительно спектрального состава излучения абсолютно черного тела. Из экспериментальных кривых зависимости функции 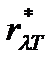от длины волны 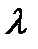при различных температурах следует, что распределение энергии в спектре излучения черного тела является неравномерным. Все кривые имеют явно выраженный максимум, который по мере повышения температуры смещается в сторону более коротких волн. Площадь, ограниченная кривой зависимости 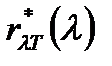и осью абсцисс 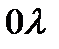, пропорциональна энергетической светимости 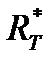абсолютно черного тела. Немецкий физик В. Вин, опираясь на законы термодинамики и электродинамики, показал, что функция спектрального распределения должна иметь вид: 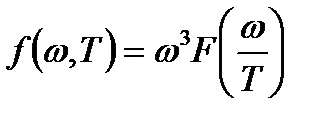, где 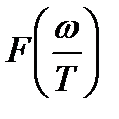− неизвестная функция отношения частоты к температуре. Формула зависимости спектральной плотности энергии равновесного излучения от его частоты, полученная Вином: 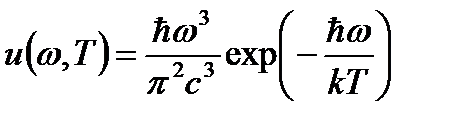, носит название формулы Вина и дает хорошее согласие с экспериментом в области достаточно больших частот. Закон смещения Вина устанавливает зависимость длины волны 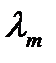, соответствующей максимуму функции 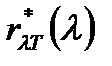, от температуры 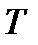: 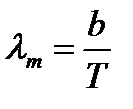, т.е. длина волны 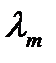, на которую приходится максимум функции испускательной способности абсолютно черного тела 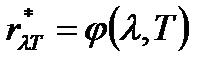, обратно пропорциональна абсолютной температуре 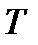этого тела; 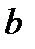− постоянная Вина, ее экспериментальное значение 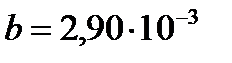м∙К. Формула Рэлея-Джинса для равновесной плотности энергии теплового излучения: 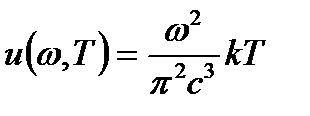и для испускательной способности абсолютно черного тела: 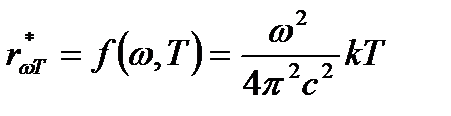. Формула Рэлея-Джинса удовлетворительно согласуется с экспериментальными данными лишь при больших длинах волн (малых частотах), и резко расходится с опытом для малых длин волн. Интегрирование выражения по 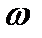в пределах от 0 до 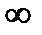дает для равновесной плотности энергии 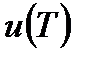бесконечно большое значение. Этот результат, получивший название ультрафиолетовой катастрофы, также находится в противоречии с опытом. Равновесие между излучением и излучающим телом устанавливается при конечных значениях .

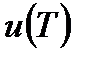5. Гипотеза Планка и формула Планка. Квантовая теория равновесного излучения.Правильное, согласующееся с опытными данными выражение для равновесной плотности энергии теплового излучения было получено немецким физиком М. Планком. Для этого ему пришлось отказаться от представлений классической физики, согласно которым энергия любой системы может изменяться непрерывно, и допустить, что электромагнитное излучение испускается в виде отдельных порций энергии − квантов, величина которых пропорциональна частоте излучения: 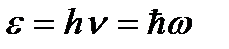, где 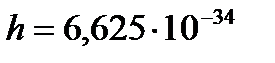Дж∙с − постоянная Планка, 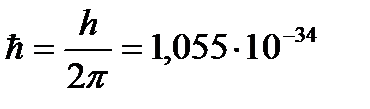Дж∙с − приведенная постоянная Планка. Формулы Планка для равновесной плотности энергии теплового излучения и универсальной функции Кирхгофа (или испускательной способности абсолютно черного тела) соответственно: , , .

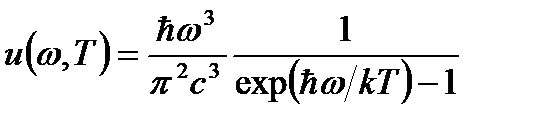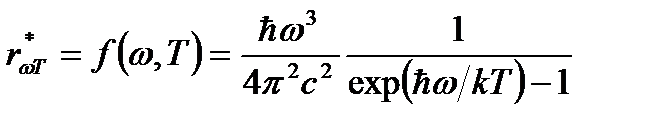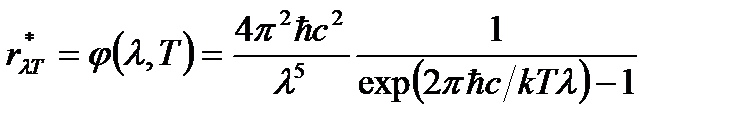Формула Планка не только согласуется с экспериментальными данными во всем интервале частот от 0 до 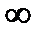, но и позволяет получить законы теплового излучения, а также вычислить постоянные в законах теплового излучения. Таким образом, формула Планка дает полное описание равновесного теплового излучения.

Законы теплового излучения и формулы Вина и Рэлея-Джинса как следствия формулы Планка.

7. Фотоэлектрический эффект. Экспериментальные законы внешнего фотоэффекта. Внутренний фотоэффект. Применение. Фотоэффектом называется явление высвобождения электронов под действием электромагнитного излучения (фотонов), сопровождающееся его(их)поглощением. Внеш.ФЭ-пр-с вых.эл-ов с пов-ти вещ.под дейст. света.При внутр.ФЭ эл-ны, выбив. Под дейст.излуч.из атомов не покидают пределы вещ.,а стан.эл-ами проводимости,а само вещ.не теряет электронейтральность.Рис.в тетр. Ч/з кварц.окно УФ излуч.попад.на фотокатод. В рез.ФЭ с пов.катода выбив.фотоэл-ны,они разгон.эл.полем. При увел.U м/у К и А все больш.частьэл-ов попад.на анод, след увел. Сила фототока. Когда всеэл-ны, выбив.с пов-ти К, дост.А,фототок вых.на насыщ.При смене полярности подкл. Фотоэл-ны не разгон., а тормозят полем и вел.фототока уменьш.Напряжение, при кот.фототок равен нулю, наз.задерживающее.Экспериментальные законы ФЭ: 1. При фиксир.пад.света фототок насыщ.прямопропорц.эн-ой освещ.фотокатода: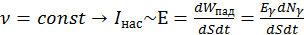

2.мах кинет.эн.фотоэл-на лин.завис.от частоты пад.света, но не завис.от его интенсивности. 3. У каждого вещ.фотокатода сущ.красная границаФЭ,при кот.ФЭ еще возможен. Кр.граница ФЭ завис.от материала и сост.пов-ти фотокатодов. Применение: Внеш.ФЭ исп. В вакуумных фотоэл.,фотоэлектронных умножителях. Внутренний ФЭ: в полупроводниках и диэлектриках