Определение концентрации сахара в растворе

1*. Приготовьте раствор сахара:

Масса сахара 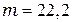г;

Объем раствора 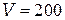мл.

Парциальная плотность 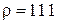кг/м³.

2*. Залейте раствор в кювету (объект 44, длина 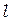= 0,120 м).

3*. Удалите с излучателя линзу-насадку (объект 42), если она установлена. Установите фотодатчик (объект 38) в поворотном столе (объект 13) на оптическую скамью комплекса ЛКО-5 в крайнее правое положение.

4*. Подключите фотодатчик к микроамперметру и включите излучатель. Убедитесь в том, что отсутствует «зашкаливание» микроамперметра на шкале 200 мкА (или 2000 мкА), когда на индикаторе гаснут все цифры кроме единицы.

Внимание! Пункты, помеченные звёздочкой, выполняет преподаватель или лаборант.

5. Установите сразу после излучателя поляризатор (объект 37) в кассете поворотного держателя (модуль 10). Подберите ориентацию поляризатора по максимуму показаний микроамперметра.

6. Установите перед фотодатчиком анализатор в поворотном держателе (модуль 12). Поворачивая анализатор вокруг оптической оси, убедитесь в том, что существуют минимальные 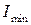и максимальные 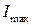показания микроамперметра. Запишите их значения. Перекройте рукой пучок излучения и зафиксируйте фоновый отсчет .

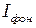7. Установите минимальное 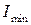значение показаний миллиамперметра, иными словами «скрестите» поляризаторы и запишите значение угла 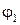по шкале анализатора.

8. Установите между поляризатором и анализатором кювету с раствором сахара. При этом показания миллиамперметра возрастут, или как говорят, поле «просветлится». Запишите показания миллиамперметра .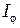

9. Поворотом анализатора снова добейтесь минимальных показаний миллиамперметра. Запишите угол 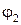, при котором достигается это минимум. Повторите измерения не менее трёх раз. Все данные занесите в таблицу.

Таблица

	Без кюветы	С кюветой

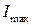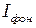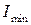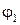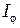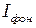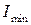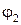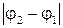10. По формуле:

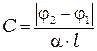
рассчитайте концентрацию 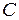сахара, используя постоянную вращения плоскости поляризации

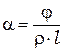=0,45 град/(кг/м²)

и длину кюветы 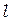=0,120 м.

11. Найдите среднее значение 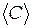, и по формуле Стьюдента рассчитайте погрешность измерений.

11. Запишите результат в формате:

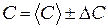
Контрольные вопросы

1.Что такое естественный свет? Как колеблется электрический вектор естественного света?

2. Что такое поляризованный свет? Какие существуют виды поляризации?

3. Как изменяются интенсивности естественного и поляризованного света при прохождении через идеальный поляризатор? Закон Малюса.

6. Поляризация при отражении света от диэлектрика. Закон Брюстера. Стопа Столетова.

7. Двойное лучепреломление. Свойства обыкновенного и необыкновенного лучей.

8. Прохождение плоскополяризованного света через одноосную кристаллическую пластинку. Оптическая разность хода и разность фаз обыкновенного и необыкновенного лучей на выходе из кристалла.

9. Какие существуют способы получения поляризованного света.

10. Как объяснить механизм вращения плоскости поляризации оптически активными веществами?

11. Какие существуют методы измерения угла поворота плоскости поляризации световой волны оптически активной средой?

5. ЛАБОРАТОРНАЯ РАБОТА№ 3-27
ОПРЕДЕЛЕНИЕ УГЛА БРЮСТЕРА

Цели работы: изучение поляризации света при отражении от поверхности диэлектрика, определение угла Брюстера.

Приборы и принадлежности: лабораторный комплекс ЛКО-5.

Методика эксперимента

При наклонном падении света на поверхность диэлектрика коэффициент отражения 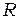волн с поляризацией в плоскости падения отличается от коэффициента отражения волн с поляризацией, перпендикулярной плоскости падения. На рис. 1. условно обозначены стрелками – колебания вектора 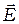в плоскости падения, точками – перпендикулярно плоскости падения.

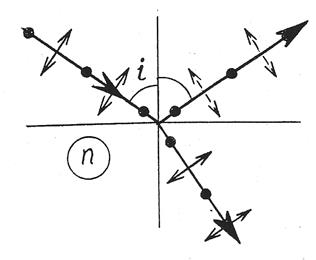
Рис. 1.

На рис. 2 приведены графики зависимостей коэффициентов отражения от угла падения. Существует угол падения, называемый углом Брюстера 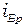, при котором 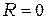, т.е. волна с поляризацией в плоскости падения вообще не отражается. Это случается, когда отраженный и преломлённый лучи ортогональны. Рассматривая отражённую волну как результат излучения дипольных моментов атомов диэлектрика, колеблющихся под действием электрического поля прошедшей (преломлённой) волны и учитывая, что в направлении своих колебаний диполи не излучают, мы можем объяснить отсутствие отраженной волны, показанной на рис. 1 пунктиром (см. эффект Брюстера – раздел 3)

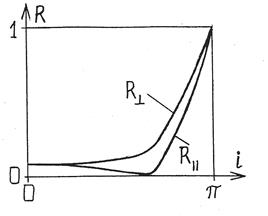
Рис. 2.

Из законов геометрической оптики следует:

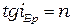(1)

где 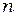- показатель преломления диэлектрика. При этом прошедший свет будет частично поляризован, а отраженный свет будет частично поляризован, если 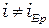, и полностью поляризован, если 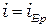. Измерив, экспериментально угол Брюстера по формуле (1) можно рассчитать показатель преломления диэлектрика.

Порядок выполнения работы

Лабораторная работа выполняется на модульном учебном комплексе ЛКО-5. Перед началом работы необходимо ознакомиться с описанием комплекса, инструкцией по его эксплуатации и техники безопасности в Приложении № 3.

Задание 1

1. Удалите с излучателя линзу-насадку (объект 42), если она установлена.

2. Установите на оптическую скамью сразу после излучателя поляризатор (объект 12).

3. За поляризатором на оптическую скамью установите пластмассовую пластину (объект 6) в поворотном столе (модуль 13) перпендикулярно оптической оси.

4*. Включите лазерный источник.

Внимание! Пункты, помеченные звёздочкой, выполняет преподаватель или лаборант.

5. Поворачивая стол, наблюдайте визуально за поведением интенсивности отраженного от пластинки лазерного пучка на фронтальном экране. Если не наблюдается выраженного минимума интенсивности отражённого луча, подберите с помощью поляризатора (объект 12) такую поляризацию излучения, чтобы в падающем на пластинку излучении вектор 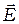колебался в плоскости падения. В нашем случае это горизонтальная плоскость. Направление 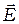совпадает с направлением рукоятки поворота поляризатора (объект 12).

6. Зафиксируйте угловое положение стола, отвечающее минимуму отражения, подстройте поляризацию падающего света и ещё раз уточните положение минимума. Запишите значение угла 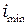по шкале поворотного стола

7. Определите положение нормали к пластинке, для этого пустите отражённый луч навстречу падающему лучу и запишите значение угла .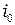

8. Найдите угол Брюстера по формуле:

.

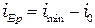9. По формуле (1) рассчитайте показатель преломления пластины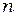

10. Оцените погрешность и запишите результат в формате:

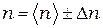
Задание 2

1. Установите вместо пластмассовой пластины (объект 6) последовательно объекты 4, 5, 7, 8 или 9 из набора объектов комплекса ЛКО-1 (не менее трёх, по указанию преподавателя).

2. Используя методику задания 1, измерьте угол Брюстера для выбранных объектов.

Контрольные вопросы

1.Что такое естественный свет? Как колеблется электрический вектор естественного света?

2. Что такое поляризованный свет? Какие существуют виды поляризации?

3. Как изменяются интенсивности естественного и поляризованного света при прохождении через идеальный поляризатор? Закон Малюса.

6. Поляризация при отражении света от диэлектрика. Закон Брюстера. Стопа Столетова.

7. Двойное лучепреломление. Свойства обыкновенного и необыкновенного лучей.

8. Прохождение плоскополяризованного света через одноосную кристаллическую пластинку. Оптическая разность хода и разность фаз обыкновенного и необыкновенного лучей на выходе из кристалла.

9. Какие существуют способы получения поляризованного света.

10. Как объяснить механизм вращения плоскости поляризации оптически активными веществами?

11. Какие существуют методы измерения угла поворота плоскости поляризации световой волны оптически активной средой?

6. ЛАБОРАТОРНАЯ РАБОТА№ 3-28
ЭЛлиПТИЧЕСКАЯ ПОЛЯРИЗАЦИЯ

Цели работы: изучение прохождения света через кристаллическую пластинку.

Приборы и принадлежности: лабораторный комплекс ЛКО-5.

Методика эксперимента

При прохождении света через анизотропные среды, в частности, через кристаллы, поляризация излучения может изменяться. В каждом кристалле существуют три взаимно ортогональных направления, называемые главными осями кристалла, обладающие важным свойством: если волна линейно поляризована и колебания вектора 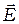направлены вдоль одной из главных осей, то поляризация волны при прохождении через кристалл не изменяется. Для разных главных осей показатели преломления, а значит и скорости распространения волн, различны.

Воспользуемся этим для получения света с эллиптической поляризацией. Пусть свет проходит через кристаллическую пластинку, главные оси которой направлены по осям х и y, соответствующие показателям преломления и , лежат в плоскости пластинки, а третья ось z нормальна к пластинке. Направим пучок света вдоль оси z (рис.68).

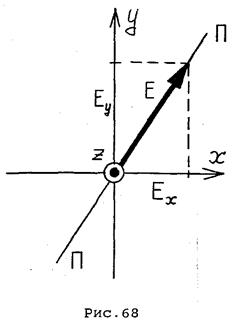
Поле 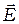падающей волны разложим на составляющие

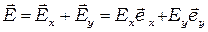
где 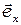и 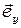единичные векторы по осям 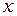и 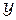. Волна с полем 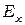затратит на прохождение пластинки время 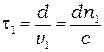, а волна с 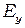- время 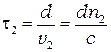, в итоге одна волна опередит другую на время 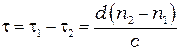, что приведёт к дополнительному сдвигу фаз колебани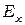й и 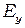на величину

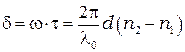
Тот же результат можно получить по-другому: для двух волн пластина создает разность хода

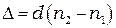
и разность фаз

.

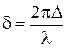Если 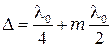пластинку называют четвертьволновой. Если 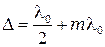- пластинку называют полуволновой.

Если в линейно поляризованной падающей волне вектор 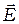уже направлен вдоль одной из главных осей х или у, то амплитуда колебаний вдоль другой оси равна нулю, и на выходе из пластинки имеем лишь ту составляющую вектора 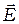, что и на входе, т.е. поляризация волны не изменится. Если же на входе обе компоненты 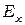и 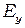не равны нулю, то поляризация на выходе определяется соотношением их амплитуд и полученной разностью фаз .

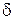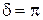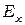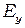При (полуволновая пластинка) синфазные колебания и на входе в пластинку превращаются в противофазные на выходе.

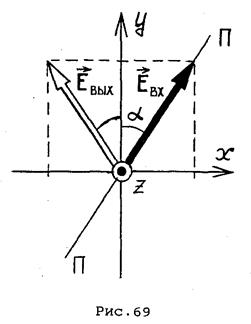
Это приводит к повороту плоскости поляризации на угол 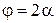, где 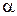- угол между главной осью пластинки и плоскостью поляризации падающей волны (рис.69). Если повернуть пластинку вокруг оси 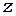, плоскость поляризации на выходе повернется на вдвое больший угол.

Если 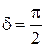(четвертьволновая пластинка) и угол 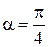, то на выходе получим ортогональные колебания равных амплитуд ( 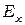= 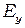) с фазовым сдвигом 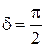, что соответствует круговой поляризации.

Если вносимая пластинкой разность хода заранее неизвестна (таков объект 39), её можно определить по анализу поляризации после пластинки следующим образом. Определим положение главных осей пластинки и установим их под углом 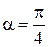к плоскости поляризации падающего света, определяемой входным поляризатором П1 (рис. 70).

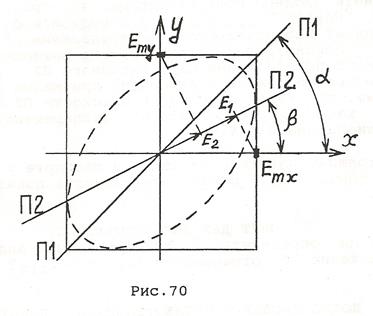
После пластинки получим колебания с одинаковыми амплитудами и со сдвигом фаз 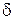, который следует найти. Установим после пластинки поляризатор П2. Через него пройдут колебания с амплитудам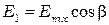и

и ,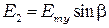

где угол 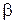определяет ориентацию поляризатора (см. рис. 70). Интенсивность прошедшей через поляризатор волны определяется этими амплитудами, а также разностью фаз колебаний (см. методическое пособие - “Интерференция”):

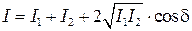
Учитывая, что 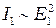а 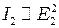и модули амплитуды 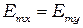, получаем:

.

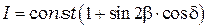Поворачивая поляризатор П2, найдем максимальное и минимальное значение интенсивности прошедшего через него излучения. Поскольку

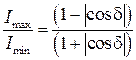
находим:

.

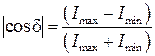Для однозначного определения 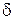нужно знать возможный диапазон значений толщины пластины. Известно, что для объекта 39 разность хода .

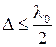Задание 1