Квантовая теория атома водорода
34.1. Модель атома Резерфорда-Бора
Резерфорд предложил ядерную(планетарную) модель атома. Согласно этой модели, вокруг положительного ядра, имеющего заряд Ζе (Ζ — порядковый номер элемента в системе Менделеева, е — элементарный заряд), размер 10-15 – 10-14 м и массу, практически равную массе атома. В области с линейными размерами порядка 10-10 м по замкнутым орбитам движутся электроны, образуя электронную оболочку атома. Так как атомы нейтральны, то заряд ядра равен суммарному заряду электронов, т. е. вокруг ядра должно вращаться Ζ электронов.
Считаем, что электрон движется вокруг ядра по круговой орбите радиуса r. При этом кулоновская сила взаимодействия между ядром и электроном сообщает электрону центростремительное ускорение. Второй закон Ньютона для электрона, движущегося по окружности под действием кулоновской силы, имеет вид:
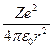 =
= 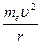 , (34.1)
, (34.1)
где mе, и υ — масса и скорость электрона на орбите радиуса r, ε0 — электрическая постоянная.
Уравнение (34.1) содержит два неизвестных: r и υ. Следовательно, существует бесчисленное множество значений радиуса и соответствующих ему значений скорости а значит, и энергии, удовлетворяющих этому уравнению. Поэтому величины r, υ (следовательно, и Е) могут меняться непрерывно, т. е. может испускаться любая, а не вполне определенная порция энергии. Тогда спектры атомов должны быть сплошными. В действительности же опыт показывает, что атомы имеют линейчатый спектр. Из выражения (34.1) следует, что при r~10-10 м скорость движения электронов - υ~106 м/с, а ускорение ~ 1022 м/с2. Согласно классической электродинамике, ускоренно движущиеся электроны должны излучать электромагнитные волны и вследствие этого непрерывно терять энергию. В результате электроны будут приближаться к ядру и, в конце концов, упадут на него. Таким образом, атом Резерфорда оказывается неустойчивой системой, что опять-таки противоречит действительности.
Попытки построить модель атома в рамках классической физики не привели к успеху. Преодоление возникших трудностей потребовало создания качественно новой — квантовой— теории атома.
Исследования спектров излучения разреженных газов (т. е. спектров излучения отдельных атомов) показали, что каждому газу присущ определенный линейчатый спектр, состоящий из отдельных спектральных линий или групп близко расположенных линий. Самым изученным является спектр наиболее простого атома — атома водорода.
И. Бальмер подобрал эмпирическую формулу, описывающую все известные в то время спектральные линии атома водорода в видимой области спектра:
ν= R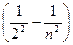 (n =3, 4, 5, ...), (34.2)
(n =3, 4, 5, ...), (34.2)
где R =3,29×1015 с-1 —постоянная Ридберга.
Из выражения (34.2) вытекает, что спектральные линии, отличающиеся различными значениями п, образуют группу или серию линий, называемую серией Бальмера.
В спектре атома водорода было обнаружено еще несколько серий.
В ультрафиолетовой области спектра находится серия Лаймана:
ν= R 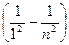 (n =2, 3, 4, 5, ...),
(n =2, 3, 4, 5, ...),
В инфракрасной области спектра были также обнаружены:
Серия Пашена ν= R 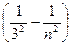 (n = 4, 5, 6,...),
(n = 4, 5, 6,...),
Серия Брэкета ν= R 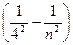 (n = 5, 6, 7,...),
(n = 5, 6, 7,...),
Серия Пфунда ν= R 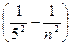 (n = 6, 7, 8,...),
(n = 6, 7, 8,...),
Серия Хэмфри ν= R 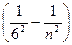 (n = 7, 8, 9,...),
(n = 7, 8, 9,...),
Все приведенные выше серии в спектре атома водорода могут быть описаны одной формулой, называемой обобщенной формулой Бальмера:
ν = R 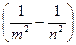 , (34.3)
, (34.3)
где тимеет в каждой данной серии постоянное значение, т = 1, 2, 3, 4, 5, 6 (определяет серию), п принимает целочисленные значения начиная с т+1 (определяет отдельные линии этой серии).
Приведенные выше сериальные формулы подобраны эмпирически и долгое время не имели теоретического обоснования, хотя и были подтверждены экспериментально с очень большой точностью.
Постулаты Бора
Первая попытка построить качественно новую — квантовую — теорию атома предпринята Нильсом Бором. Он поставил перед собой цель связать в единое целое эмпирические закономерности линейчатых спектров, ядерную модель атома Резерфорда и квантовый характер излучения и поглощения света. В основу своей теории Бор положил два постулата.
Первый постулат Бора (постулат стационарных состояний): в атоме существуют стационарные (не изменяющиеся со временем) состояния, в которых он не излучает энергии. Стационарным состояниям атома соответствуют стационарные орбиты, по которым движутся электроны. Движение электронов по стационарным орбитам не сопровождается излучением электромагнитных волн.
В стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь дискретные квантованные значения момента импульса, удовлетворяющие условию
mе υ rn = n ћ (n= 1, 2, 3,…) (34. 4)
где mе, — масса электрона, υ — его скорость по n -й орбите радиуса rn, ћ=h/2π.
Второй постулат Бора (правило частот): при переходе электрона с одной стационарной орбиты на другую излучается (поглощается) один фотон с энергией
hv = Е n -Еm (34.5)
равной разности энергии соответствующих стационарных состояний (Е n и Еm — соответственно энергии стационарных состояний атома до и после излучения (поглощения)). При Еm < Еn происходит излучение фотона (переход атома из состояния с большей энергией в состояние с меньшей энергией, т. е. переход электрона с более удаленной от ядра орбиты на более близлежащую), при Еm >Еn, —его поглощение (переход атома из состояния с меньшей энергией в состояние с большей энергией, т. е. переход электрона на более удаленную от ядра орбиту). Набор возможных дискретних частот v = (Еn -Еm)/h квантовых переходов и определяет линейчатый спектр атома.
34.3. Спектр атома водорода по Бору
Постулаты, выдвинутые Бором, позволили рассчитать спектр атома водорода и водородоподобных систем — систем, состоящих из ядра с зарядом Zе и одного электрона (например, ионы Не+ , Lі2+ ), а также теоретически вычислить постоянную Ридберга.
Рассмотрим движение электрона в водородоподобной системе, ограничиваясь круговыми стационарными орбитами.
Радиус n-й стационарной орбиты:
rn = n2 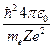 , (34.6)
, (34.6)
где n = 1, 2, 3, ... . Из выражения (34.6) следует, что радиусы орбит растут пропорционально квадратам целых чисел.
Для атома водорода (Z=1) радиус первой орбиты электрона при п=1, называемый первым боровским радиусом, равен
r1 = а = 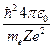 = 52,8 пм, (34.7)
= 52,8 пм, (34.7)
Полная энергия электрона в водородоподобной системе складывается из его кинетической энергии (mеυ2/2) и потенциальной энергии в электростатическом поле ядра (-Ze2/4πε0r):
Е =(mеυ2/2) - (Ze2/4πε0r)= -½(Ze2/4πε0r)
учли, что (mеυ2/2) = ½(Ze2/4πε0r). Учитывая квантованные для радиуса n-й стационарной орбиты значения (34.6), получим, что энергия электрона может принимать только следующие дозволенные дискретные значения:
Еn = - 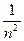
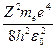 (n= 1,2,3,…), (34.8)
(n= 1,2,3,…), (34.8)
где знак минус означает, что электрон находится в связанном состоянии.
Из формулы (34.8) следует, что энергетические состояния атома образуют последовательность энергетических уровней, изменяющихся в зависимости от значения п. Целое число n в выражении (34.8), определяющее энергетические уровни атома, называется главным квантовым числом. Энергетическое состояние с п=1 является основным (нормальным) состоянием; состояния с n>1 являются возбужденными. Энергетический уровень, соответствующий основному состоянию атома, называется основным (нормальным) уровнем; все остальные уровни являются возбужденными.
Придавая n различные целочисленные значения, получим для атома водорода (Z = 1), согласно формуле (33.8), возможные уровни энергии. Энергия атома водорода с увеличением n возрастает и энергетические уровни сближаются к границе, соответствующей значению n=∞. Атом водорода обладает, таким образом, минимальной энергией (Е1=-13,55эВ) при п=1 максимальной (Е∞ =0) при п= ∞. Следовательно, значение Е∞ =0 соответствует ионизации атома (отрыву от него электрона). Согласно второму постулату Бора, при переходе атома водорода (Z= 1) из стационарного состояния п в стационарное состояние т с меньшей энергией испускается квант
hν=Е n -Еm = - 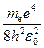
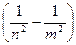 ,(34.9)
,(34.9)
откуда частота излучения
ν = 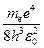
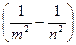 = R
= R 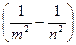 ,(34.10)
,(34.10)
где R= 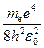 .
.
Воспользовавшись при вычислении R современными значениями универсальных постоянных, получим величину, совпадающую с экспериментальным значением постоянной Ридберга в эмпирических формулах для атома водорода.
Подставляя, например, в формулу (34.10) m =1 и п=2, 3, 4, ..., получим группу линий, образующих серию Лаймана и соответствующих переходам электронов с возбужденных уровней (n=2, 3, 4, ...) на основной (m=1). Аналогично, при подстановке m = 2, 3, 4, 5, 6 и соответствующих им значений n получим серии Бальмера, Пашена, Брэкета, Пфунда и Хэмфри.
Следовательно, по теории Бора, спектральные серии соответствуют излучению, возникающему в результате перехода атома в данное состояние из возбужденных состояний расположенных выше данного.
Спектр поглощения атома водорода является линейчатым, но содержит при нормальных условиях только серию Лаймана. Он также объясняется теорией Бора. Так как свободные атомы водорода обычно находятся в основном состоянии (стационарное состояние с наименьшей энергией при n=1), то при сообщении атомам извне определенной энергии могут наблюдаться лишь переходы атомов из основного состояния в возбужденные (возникает серия Лаймана).
Теория Бора обладает внутренними противоречиями (с одной стороны, применяет законы классической физики, а с другой — основывается на квантовых постулатах). В теории Бора рассмотрены спектры атома водорода и водородоподобных систем и вычислены частоты спектральных линий, однако эта теория не смогла объяснить интенсивности спектральных линий и ответить на вопрос: почему совершаются те или иные переходы? Серьезным недостатком теории Бора была невозможность описания с ее помощью спектра атома гелия — одного из простейших атомов, непосредственно следующего за атомом водорода.
