Аналогія між величинами, які характеризують поступальний і обертальний рухи
МІНІСТЕРСТВО ОСВІТИ ТА НАУКИ УКРАЇНИ
ПРИДНІПРОВСЬКА ДЕРЖАВНА АКАДЕМІЯ БУДІВНИЦТВА ТА АРХІТЕКТУРИ
Кафедра фізики
МЕТОДИЧНІ ВКАЗІВКИ
До виконання модульних завдань з курсу фізики для студентів
Денної форми навчання
Дніпропетровськ – 2009
Методичні вказівки до виконання модульних завдань з курсу фізикидля студентів денної форми навчання всіх спеціальностей. / Укладачі: Романець Р.Г, Карасьов Г.Г., Подолинський В.В., Волнянська І.П., Побединська М.П. – Дніпропетровськ: ПДАБА. 2009р. – 15с.
Пропоновані методичні вказівки призначені для використання в умовах упровадження кредитно-модульної системи навчання. Він включає матеріали для вивчення курсу фізики в першому семестрі двосеместрового курсу фізики. Ці матеріали розбиті на три навчальні модулі. Відмітна особливість даних методичних вказівок полягає в тому, що основну увагу приділено конкретній модульно-рейтинговій навчальній технології проведення занять з курсу фізики для інженерних спеціальностей. Методичні вказівки дають змогу використовувати їх студентами як в аудиторній, так і в самостійній роботі.
Укладачі: Р.Г.Романець, кандидат фізико-математичних наук, доцент,
професор кафедри фізики ПДАБА;
Г.Г.Карасьов, кандидат фізико-математичних наук, доцент,
кафедри фізики ПДАБА;
В.В.Подолінський, кандидат фізико-математичних наук, доцент,
кафедри фізики ПДАБА;
І.П.Волнянська, асистент кафедри фізики ПДАБА.
М.П.Побединська, асистент кафедри фізики ПДАБА.
Відповідальний за випуск:Б.М.Дікарев, кандидат фізико-математичних
наук, професор, зав. кафедри фізики ПДАБА.
Рецензент: І.П.Гаркуша, професор, зав. кафедри фізики НГУ.
Затверджено
на засіданні кафедри фізики ПДАБА.
Протокол № 8 від 16.04.2009р.
Зав. кафедри фізики Дикарев Б.М.
Затверджено
на засіданні Президії методичної ради ПДАБА.
Протокол № від 2009р.
Пропоновані методичні вказівки призначені для використання в умовах упровадження кредитно-модульної системи навчання. Він включає матеріали для вивчення курсу фізики в першому семестрі двосеместрового курсу фізики. Вивчення курсу фізики відбувається на протязі 18 тижнів і розподіляється на три модулі.
Першому модулю відповідає розділ „Фізичні основи механіки” і він розрахований на 6 учбових тижнів. На протязі цього відрізку навчання студенти розв’язують задачі циклу 1 на розділ курсу фізики „Кінематика поступального і обертального рухів”; циклу 2 на розділ „Динаміка”, циклу 3 „Обертальний рух. Деформація твердих тіл”. На останньому тижні першого модуля за результатами поточної успішності і контрольної роботи студенту виставляється модульна рейтингова оцінка.
Другому модулю відповідають розділи „Молекулярна фізика” і „Термодинаміка” і цей модуль теж розрахований на 6 учбових тижнів. На протязі цього відрізку навчання студенти розв’язують задачі циклу 4 на розділ курсу фізики „Молекулярна фізика” і циклу 5 на розділ „Термодинаміка”. На останньому тижні другого модуля за результатами поточної успішності і контрольної роботи студенту виставляється модульна рейтингова оцінка.
Третьому модулю відповідають розділи „Електростатика” , „Постійний струм” , „Магнітне поле” і цей модуль розрахований на 6 тижнів. На протязі цього відрізку навчання студенти розв’язують задачі циклу 6 на розділ „Електростатика”, циклу 7 на розділ „Постійний струм”, задачі циклу 8 на розділ „Магнітне поле” і циклу 9 на розділ „Електромагнітна індукція”. На останньому тижні третього модуля за результатами поточної успішності і контрольної роботи студенту виставляється модульна рейтингова оцінка.
Данні методичні вказівки дають змогу студентам планувати свій навчальний процес, орієнтуватися у різних розділах курсу фізики. Перед використанням задач з відповідних циклів студентам пропонуються основні фізичні формули, які вони можуть застосовувати при розв’язанні задач як в аудиторній, так і в самостійній роботі.
Механіка
Лінійне прискорення 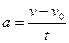 ,
, 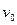 - початкова швидкість. Кутове прискорення
- початкова швидкість. Кутове прискорення 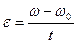 , де кутова швидкість
, де кутова швидкість  ,
, 
 число обертів за одиницю часу,
число обертів за одиницю часу,  - початкова кутова швидкість.
- початкова кутова швидкість.
Лінійний шлях 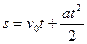 . Кутовий шлях
. Кутовий шлях 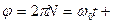
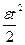
 , де
, де  - загальне число обертів за час
- загальне число обертів за час  .
.
Другий закон Ньютона для поступального руху  . Другий закон Ньютона для обертального руху
. Другий закон Ньютона для обертального руху 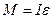 , де момент сили
, де момент сили  ,
, 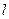 - плече сили.
- плече сили.
Момент інерції диска відносно осі симетрії 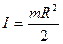 , -
, - 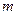 - маса і
- маса і  радіус диска. Момент інерції стержня відносно перпендикулярної осі, що проходить через середину стержня
радіус диска. Момент інерції стержня відносно перпендикулярної осі, що проходить через середину стержня  , де
, де 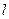 - довжина стержня.
- довжина стержня.
Кінетична енергія диска, що котиться, складається з кінетичної енергії поступального руху 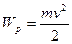 і кінетичної енергії обертального
і кінетичної енергії обертального  руху
руху  .
.
Імпульс тіла 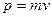 , імпульс сили
, імпульс сили  . Момент імпульсу
. Момент імпульсу  .
.
Сила тяжіння 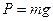 , де
, де 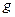 =9.8 м/с
=9.8 м/с  . За законом всесвітнього тяжіння
. За законом всесвітнього тяжіння 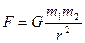 , де гравітаційна стала
, де гравітаційна стала  =6.67*10
=6.67*10 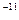 -Н*м
-Н*м  /кг
/кг  . Якщо на тіло діє сила тяжіння
. Якщо на тіло діє сила тяжіння  і сила натягу
і сила натягу  , рівняння динаміки для прискореного руху вниз має вигляд
, рівняння динаміки для прискореного руху вниз має вигляд 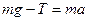 , а при русі вгору цим рівнянням буде
, а при русі вгору цим рівнянням буде  .
.
Механічне напруження  , де
, де  - модуль Юнга. Потенціальна енергія пружно деформованого тіла
- модуль Юнга. Потенціальна енергія пружно деформованого тіла 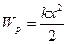 . Молекулярна фізика і термодинаміка
. Молекулярна фізика і термодинаміка
Рівняння Менделєєва-Клапейрона 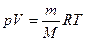 , універсальна газова стала
, універсальна газова стала  8.31 Дж/(моль*К).
8.31 Дж/(моль*К).
Об’єднаний газовий закон 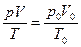 , для ізотермічного процесу
, для ізотермічного процесу  const і
const і  ; для ізобарного процесу
; для ізобарного процесу  const і
const і  ; для ізохорного процесу
; для ізохорного процесу 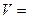 const і
const і 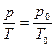 . Густина речовини
. Густина речовини 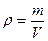 . Кількість молекул газу
. Кількість молекул газу  , де число Авогадро
, де число Авогадро 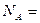 6.02*10
6.02*10  1/кмоль.
1/кмоль.  Середня енергія однієї молекули
Середня енергія однієї молекули  , число ступенів вільності
, число ступенів вільності 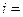 3 (поступальні) для одноатомної молекули,
3 (поступальні) для одноатомної молекули, 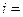 5 (3 поступальні і 2 обертальні) для двоатомної молекули,ри. Больцмана
5 (3 поступальні і 2 обертальні) для двоатомної молекули,ри. Больцмана 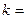 1.38*10
1.38*10  Дж/К.
Дж/К.
Перший закон термодинаміки  , елементарна кількість теплоти при
, елементарна кількість теплоти при 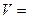 const,
const,  ; при
; при  const,
const,  , де
, де  - молярні теплоємності при сталих
- молярні теплоємності при сталих 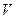 і
і 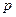
Зміна внутрішньої енергії,  ,
, 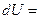 0 при
0 при  const. Елементарна робота
const. Елементарна робота 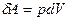 ,
, 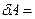 0 при
0 при 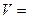 const. В адіабатному процесі
const. В адіабатному процесі  0. К.к.д. ідеальної теплової машини
0. К.к.д. ідеальної теплової машини  .
.
Аналогія між величинами, які характеризують поступальний і обертальний рухи
| Фізична величина | Поступальний рух (I) | Обертальний рух (II) | Зв’язок |
| Переміщення Шлях | лінійне  лінійний лінійний 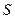 | кутове  кутовий кутовий  | 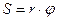 |
| Швидкість | лінійна 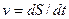 | кутова 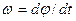 |  |
| Прискорення | тангенціальне 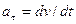 | кутове  нормальне нормальне  | 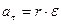 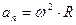 |
| Результуюча сила (I) Момент сили (II) |  | 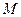 |  |
| Швидкість (I) Швидкість (II) | 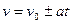 | 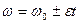 | |
| Шлях (I) Шлях (II) |  | 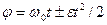 | |
| Швидкість (I) Швидкість (II) | 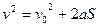 |  | |
| Маса (I) Момент інерції (II) | 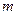 |  |  |
Імпульс (I)  Момент імпульсу (II) Момент імпульсу (II) | 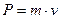 |  | |
| Другий закон Ньютона | 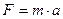  | 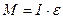  | |
Імпульс сили (I)  Момент імпульсу сили (II) Момент імпульсу сили (II) |  | 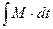 | |
Робота (I)  Робота (II) Робота (II) |  |  | |
Потужність (I)  Потужність (II) Потужність (II) |  | 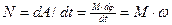 | |
Кінетична енергія (I) Кінетична енергія (II)  |  |  | |
| Потенціальна енергія | П 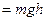 П П 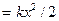 |
Цикл 1 задач з фізики на розділ „Кінематика поступального і обертального рухів”
Задача 1.1.
Першу половину часу свого руху автомобіль рухався зі швидкістю Відповідь (В):
 км/год, а другу половину часу – зі швидкістю
км/год, а другу половину часу – зі швидкістю 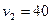 км/год.
км/год. 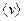 = 60 км/год.
= 60 км/год.
Яка середня швидкість 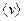 руху автомобіля?
руху автомобіля?
Задача 1.2.
Першу половину свого шляху автомобіль рухався зі швидкістю (В): 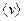 =53,3 км/год
=53,3 км/год  км/год, а другу половину шляху– зі швидкістю
км/год, а другу половину шляху– зі швидкістю 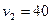 км/год.
км/год.
Яка середня швидкість 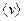 руху автомобіля?
руху автомобіля?
Задача 1.3.
На висоті  м тіло, що вільно падає, мало швидкість (В):
м тіло, що вільно падає, мало швидкість (В):  м/с.
м/с.
 м/с. Чому дорівнює швидкість тіла на висоті
м/с. Чому дорівнює швидкість тіла на висоті 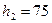 м?
м?
Задача 1.4.
Вільно падаюче тіло в останню секунду руху проходить половину (В): 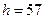 м,
м,
всього шляху. З якої висоти  падало тіло і який час
падало тіло і який час  його падіння.
його падіння.  с.
с.
Задача 1.5.
Рух матеріальної точки описується рівнянням 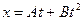 , де (В): 40 с; 80 м;
, де (В): 40 с; 80 м;
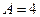 м/с,
м/с,  м/с
м/с  . Визначити момент часу, в який швидкість -0,1 м/с
. Визначити момент часу, в який швидкість -0,1 м/с  .
.
 точки дорівнює нулю. Знайти координату і прискорення в цей
точки дорівнює нулю. Знайти координату і прискорення в цей
момент.
Задача 1.6.
Залежність шляху  , який пройшло тіло, від часу
, який пройшло тіло, від часу  описується (В):
описується (В):  с;
с;
рівнянням  , де
, де 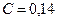 м/с
м/с  і
і  м/с
м/с  .
. 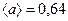 м/с
м/с  .
.
Через який час  після початку руху тіло буде мати прискорення
після початку руху тіло буде мати прискорення
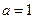 м/с
м/с  . Знайти середнє прискорення
. Знайти середнє прискорення 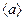 за цей проміжок часу.
за цей проміжок часу.
Задача 1.7.
Тіло кинуто горизонтально зі швидкістю 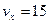 м/с. Знайти нормальне (В):
м/с. Знайти нормальне (В):  м/с
м/с 
 і тангенціальне
і тангенціальне  прискорення тіла через час
прискорення тіла через час  с після початку руху.
с після початку руху.  = 5,4м/с
= 5,4м/с 
Задача 1.8.
Тіло кинуто зі швидкістю 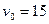 м/с під кутом
м/с під кутом  до горизонту. (В):
до горизонту. (В):  м;
м;
Не враховуючи опору повітря, знайти: 1) висоту  підйому тіла; 2)
підйому тіла; 2) 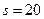 м;
м;
дальність польоту  ; 3) час підйому
; 3) час підйому  і час спуску
і час спуску  тіла.
тіла.  с.
с.
Задача 1.9.
Тіло, що обертається, збільшило свою кутову швидкість з 2,0 до (В):  с
с  .
.
64,8 рад/с за час, протягом якого відбулося 100 повних обертів.
Знайти кутове прискорення  тіла.
тіла.
Задача 1.10.
Колесо радіуса  м обертається так, що залежність кута повороту (В):
м обертається так, що залежність кута повороту (В):
радіуса колеса від часу описується рівнянням  , де
, де  рад/с;
рад/с;
 рад,
рад,  рад/с,
рад/с, 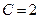 рад/с
рад/с  . Для точок на ободі колеса знайти
. Для точок на ободі колеса знайти  м/с;
м/с;
через  (с) після початку руху: а) кутову швидкість; б) лінійну
(с) після початку руху: а) кутову швидкість; б) лінійну 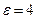 с
с  ;
;
швидкість; в) кутове прискорення; г) тангенціальне прискорення; 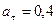 м/с
м/с  ;
;
д) нормальне прискорення. 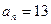 м/с
м/с  .
.
Цикл 2 задач з фізики на розділ „Динаміка”
Задача 2.1.
На рівному столі лежить брусок масою 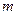 =4 кг. До бруска Відповідь (В):
=4 кг. До бруска Відповідь (В):  = 1,4 м/
= 1,4 м/  прив’язані два шнури, перекинуті через нерухомі блоки, що
прив’язані два шнури, перекинуті через нерухомі блоки, що  =11.2 Н,
=11.2 Н,  =16.8 Н
=16.8 Н
прикріплені до протилежних країв стола. До кінців шнурів
підвішені гирі, маси яких 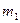 =1кг і
=1кг і 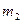 = 2 кг. Знайти приско-
= 2 кг. Знайти приско-
реня, з яким рухається брусок, і силу натягу  кожного із
кожного із
шнурів. Масою блоків і тертям знехтувати.
Задача 2.2.
Матеріальна точка масою 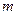 =2 кг рухається під дією деякої (В):
=2 кг рухається під дією деякої (В):  =-0.8 Н,
=-0.8 Н, 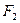 =-8 Н
=-8 Н
сили  відповідно до рівняння
відповідно до рівняння 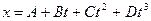 , де
, де  =0 при
=0 при  = 1.67 с
= 1.67 с
 =1 м/
=1 м/  ,
, 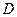 =-0.2 м/
=-0.2 м/  . Знайти значення цієї сили в моме-
. Знайти значення цієї сили в моме-
ти часу  =2 с і
=2 с і  =5 с. В який момент часу сила дорівнює
=5 с. В який момент часу сила дорівнює
нулю.
Задача 2.3.
Тіло маси 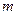 =2 кг падає вертикально з прискоренням
=2 кг падає вертикально з прискоренням  = 5 м/
= 5 м/  . (В)
. (В) 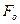 =9.6 Н.
=9.6 Н.
Визначити силу опору при русі цього тіла.
Задача 2.4.
З вершини клина, довжина якого 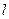 =2 м і висота
=2 м і висота  =1 м, почи- (В):
=1 м, почи- (В):  =3.63 м/
=3.63 м/  ,
,
нає сковзати невелике тіло. Коефіцієнт тертя між тілом і кли-  =1.05 с,
=1.05 с,
ном  =0.15. Визначити: 1) прискорення, з яким рухається
=0.15. Визначити: 1) прискорення, з яким рухається  =3.81 м/с
=3.81 м/с
тіло; 2) час проходження тіла вздовж клина; 3) швидкість тіла
у основи клина.
Задача 2.5.
Кулька масою 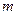 = 300 г ударяється об стіну і відскакує від неї. (В): Р= 3 Н*с
= 300 г ударяється об стіну і відскакує від неї. (В): Р= 3 Н*с
Визначити імпульс Р, який одерже стіна, якщо в останній мо-
мент перед ударом кулька мала швидкість  =10 м/с і ця швид-
=10 м/с і ця швид-
кість була направлена під кутом 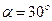 до поверхні стіни. Удар
до поверхні стіни. Удар
вважати абсолютно пружним.
Задача 2.6.
До шнура підвішено гирю маси 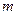 . Гирю відвели у бік так, що (В): 3
. Гирю відвели у бік так, що (В): 3 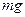 ;
;
шнур прийняв горизонтальне положення, і відпустили. Визначи- 
ти силу натягу шнура  в момент, коли шнур проходить положен-
в момент, коли шнур проходить положен-
ня рівноваги. Який кут  з вертикальною лінією складає шнур в
з вертикальною лінією складає шнур в
момент, коли сила натягу шнура дорівнює силІ тяжіння гирі?
Задача 2.7.
Автомобіль з масою 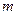 =5 т рухається зі швидкістю
=5 т рухається зі швидкістю  10 м/с по (В): 39 кН
10 м/с по (В): 39 кН
опуклому мосту. Визначити силу  тиску автомобіля на міст у
тиску автомобіля на міст у
його верхній частині, якщо радіус кривизни моста дорівнює 50 м.
Задача 2.8.
Знайти роботу  піднімання вантажу по похилій площині довжи- (В): 1.35 кДж
піднімання вантажу по похилій площині довжи- (В): 1.35 кДж
ри 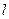 =2 м, якщо маса
=2 м, якщо маса 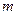 вантажу дорівнює 100 кг, кут нахилу
вантажу дорівнює 100 кг, кут нахилу 
коефіцієнт тертя  = 0.1 і вантаж рухається з прискоренням
= 0.1 і вантаж рухається з прискоренням  =1 м/
=1 м/  .
.
Задача 2.9.
Камінець рухається з найвищої точки купола, який має форму півсфери. (В): Яку дугу  описує камінець перед тим, як він відірветься від поверхні
описує камінець перед тим, як він відірветься від поверхні  купола? Тертям знехтувати.
купола? Тертям знехтувати.
Цикл 3 задач з фізики на розділи: „Обертальний рух. Деформація твердих тіл”
Задача 3.1.
Однорідний диск радіусом  м і масою
м і масою 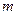 = 5 кг обертається Відповідь (В): навколо осі, яка проходить через його центр перпендикулярно до його
= 5 кг обертається Відповідь (В): навколо осі, яка проходить через його центр перпендикулярно до його  = 4,0 Н
= 4,0 Н
площини. Залежність кутової швидкості 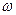 обертання диска від часу
обертання диска від часу
дається рівнянням  де
де  рад/
рад/  . Визначити дотичну
. Визначити дотичну
силу, яка прикладена до ободу диска. Тертям знехтувати.
Задача 3.2.
Маховик, момент інерції якого  63,6 кг*м
63,6 кг*м  , обертається з кутовою (В):
, обертається з кутовою (В):  100 Н*м
100 Н*м
швидкістю  31,4 рад/с. Визначити момент сил гальмування
31,4 рад/с. Визначити момент сил гальмування 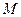 , під
, під
дією яких маховик зупиняється через час 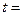 20 с. Маховик вважати
20 с. Маховик вважати
однорідним диском.
Задача 3.3.
Дві гирі з масами  2 кг і
2 кг і 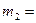 1 кг з’єднані ниткою, яка перекинута (В):
1 кг з’єднані ниткою, яка перекинута (В):  2,8 м/
2,8 м/ 
через блок масою  1 кг. Визначити прискорення
1 кг. Визначити прискорення  , з яким рухаються гирі
, з яким рухаються гирі  14,0 Н
14,0 Н
і сили натягу 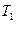 і
і  ниток, до яких підвішені гирі. Блок вважати однорідним
ниток, до яких підвішені гирі. Блок вважати однорідним 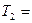 12,6 Н диском. Тертям знехтувати.
12,6 Н диском. Тертям знехтувати.
Задача 3.4.
Диск з масою  2 кг котиться без ковзання по горизонтальній площині зі (В)
2 кг котиться без ковзання по горизонтальній площині зі (В) 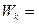 24 Дж
24 Дж
швидкістю  4 м/с. Визначити кінетичну енергію
4 м/с. Визначити кінетичну енергію  диска.
диска.
Задача 3.5.
Куля діаметром  6 см і масою
6 см і масою  0,25 кг котиться без ковзання по (В):
0,25 кг котиться без ковзання по (В): 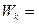 0,1 Дж
0,1 Дж
горизонтальній площині з частотою обертання  4 об/с. Визначити
4 об/с. Визначити
кінетичну енергію  кулі.
кулі.
Задача 3.6.
Колесо, яке оберталось рівно сповільнено, зменшило за час 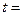 1 хв частоту (В):
1 хв частоту (В):
обертання від 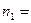 300 об/хв до
300 об/хв до 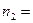 180 об/хв. Момент інерції колеса
180 об/хв. Момент інерції колеса  рад/с
рад/с 
 2 кг*м
2 кг*м  . Визначити кутове прискорення
. Визначити кутове прискорення  колеса, момент сил
колеса, момент сил  Н*м
Н*м
гальмування 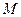 , роботу сил гальмування
, роботу сил гальмування  і число обертів
і число обертів  ,
,  Дж
Дж
яке зробило колесо за час 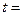 1 хв.
1 хв.  240 об
240 об
Задача 3.7.
Махове колесо починає обертатися з кутовим прискоренням  0,5 рад/с
0,5 рад/с  і (В):
і (В):  =
=
через час  с після початку руху набуває момент імпульсу
с після початку руху набуває момент імпульсу  73,5 кг*м
73,5 кг*м  /с. = 490 Дж
/с. = 490 Дж
Визначити кінетичну енергію  колеса через час
колеса через час  20 с після початку руху.
20 с після початку руху.
Задача 3.8.
Горизонтальна платформа масою 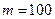 кг обертається навколо вертикальної (В): осі, яка проходить через центр платформи, з частотою
кг обертається навколо вертикальної (В): осі, яка проходить через центр платформи, з частотою  10 об/хв.Чоловік
10 об/хв.Чоловік  об/хв
об/хв
масою 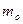 = 60 кг стоїть при цьому на краю платформи. З якою частотою
= 60 кг стоїть при цьому на краю платформи. З якою частотою  почне
почне
обертатися платформа, якщо чоловік перейде від краю платформи до її центру?
Платформу вважати однорідним диском, а чоловіка – точковою масою.
Задача 3.9.
До вертикального дроту довжиною 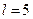 м і площею поперечного перерізу (В):
м і площею поперечного перерізу (В):  = 208 Гпа
= 208 Гпа
 мм
мм  підвішений вантаж масою
підвішений вантаж масою 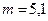 кг. В результаті цього довжина
кг. В результаті цього довжина
дроту збільшилася на 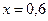 мм. Визначити модуль Юнга
мм. Визначити модуль Юнга  матеріалу дроту .
матеріалу дроту .
Цикл задач 4 з фізики на розділ „Молекулярна фізика”
Задача 4.1.
У балоні містилася маса 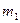 =10 кг газу під тиском
=10 кг газу під тиском  Мпа. Яку Відповідь (В):
Мпа. Яку Відповідь (В):
масу  випустили з балона, якщо тиск став рівним
випустили з балона, якщо тиск став рівним 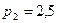 Мпа?
Мпа? 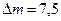 кг
кг
Температуру газу вважати сталою.
Задача 4.2.
Визначити масу 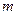 повітря, що заповнює аудиторію вистою
повітря, що заповнює аудиторію вистою  м і (В):
м і (В):
площею підлоги 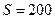 м
м  . Тиск повітря
. Тиск повітря  кПа, температура
кПа, температура 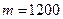 кг.
кг.
Приміщення 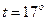 С. Молярна маса повітря М = 0,029 кг/моль.
С. Молярна маса повітря М = 0,029 кг/моль.
Задача 4.3.
При температурі  С тиск водяної насиченої пари
С тиск водяної насиченої пари 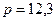 кПа. (В):
кПа. (В):
Визначити густину  водяної пари.
водяної пари.  кг/м
кг/м 
Задача 4.4.
У повітрі міститься 23,6% кисню і 76,4% азоту (за масою) під тиском (В):
 кПа при температурІ
кПа при температурІ  С. Визначити густину
С. Визначити густину  повітря і
повітря і  кг/м
кг/м 
парціальні тиски  і
і  кисню і азоту.
кисню і азоту.  кПа,
кПа,  кПа
кПа
Задача 4.5.
Молекула азоту, що летить зі швидкістю 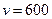 м/с пружно ударяється (В):
м/с пружно ударяється (В):
об стінку посудини по нормалі до неї. Визначити імпульс сили  Н*с
Н*с
 , який одержала стінка посудини за час удару.
, який одержала стінка посудини за час удару.
Задача 4.6.
Визначити кількість молекул 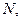 що міститься у кімнаті об’ємом
що міститься у кімнаті об’ємом  м
м  (В):
(В):
при температурі 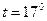 С під тиском
С під тиском  кПа.
кПа. 
Задача 4.7.
Середня квадратична швидкість молекул деякого газу 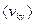 = 450 м/с. Тиск (В):
= 450 м/с. Тиск (В):
газу 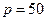 кПа. Визначити густину
кПа. Визначити густину  газу за цих умов.
газу за цих умов.  кг/м
кг/м 
Задача 4.8.
При якій температурі молекули гелію будуть мати ту ж саму середню квадратичну (В):
швидкість, що і молекули водню при температурі 20 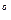 С?
С? 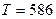 К.
К.
Задача 4.9.
Визначити середнє значення  повної кінетичної енергії однієї молекули гелію, (В):
повної кінетичної енергії однієї молекули гелію, (В):
кисню і водяної пари при температурі  К.
К.  Дж;
Дж;  Дж;
Дж; 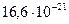 Дж.
Дж.
Задача 4.10.
Балон місткістю 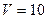 л містить водень масою
л містить водень масою 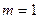 г. Визначити середню (В):
г. Визначити середню (В): 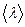 =
=
довжину вільного пробігу 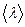 молекул. Діаметр молекули водню
молекул. Діаметр молекули водню 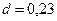 нм. = 142 нм.
нм. = 142 нм.
Задача 4.11.
На якій висоті  над поверхнею Землі атмосферний тиск вдвоє менший, (В):
над поверхнею Землі атмосферний тиск вдвоє менший, (В):
ніж на її поверхні. Вважати, що температура  повітря дорівнює 290К і
повітря дорівнює 290К і  =5,88 км.
=5,88 км.
Не змінюється з висотою.
Задача 4.12.
Вуглекислий газ і азот знаходяться за однакових температур і тисків. (В): 
Визначити для цих газів відношення: а) коефіцієнтів дифузії; 
б) в’вязкостей ; в) теплопровідностей. Діаметри молекул газів 
вважати однаковими.
Цикл задач 5 з фізики на розділ „Термодинаміка”
Задача 5.1.
Визначити теплопровідність  повітря при тиску
повітря при тиску  кПа і. Відповідь (В):
кПа і. Відповідь (В):
температурі 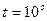 С. Діаметр молекул повітря
С. Діаметр молекул повітря  нм 13,2 мВт/(м*К)
нм 13,2 мВт/(м*К)
Задача 5.2.
Молярна маса деякого газу  кг/моль. Відношення
кг/моль. Відношення 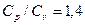 . (В):
. (В):
Визначити питомі теплоємності 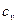 і
і  цього газу.
цього газу. 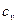 =693 Дж/(кг*К);
=693 Дж/(кг*К);  =970 Дж/(кг*К)
=970 Дж/(кг*К)
Задача 5.3.
Маса  г кисню знаходиться під тиском
г кисню знаходиться під тиском  кПа при температурі (В):
кПа при температурі (В):
 С. Після нагрівання при
С. Після нагрівання при 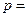 const газ зайняв об’єм
const газ зайняв об’єм  л.
л.  кДж,
кДж,
Визначити кількість теплоти  , яку одержав газ, зміну
, яку одержав газ, зміну  внутрішньої
внутрішньої 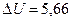 кДж,
кДж,
енергії газу і роботу  , яка була виконана газом при розширенні.
, яка була виконана газом при розширенні.  кДж.
кДж.
Задача 5.4.
Кількість 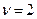 кмоль вуглекислого газу нагрівається під сталим тиском на (В):
кмоль вуглекислого газу нагрівається під сталим тиском на (В):  =50 К. Визначити зміну
=50 К. Визначити зміну  внутрішньої енергії газу, роботу
внутрішньої енергії газу, роботу 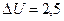 МДж,
МДж,
 розширення газу і кількість теплоти
розширення газу і кількість теплоти  яка була надана газу.
яка була надана газу. 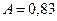 МДж,
МДж, 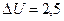 МДж,
МДж,
Задача 5.5.
При ізотермічному розширенні маси  г азоту при температурі (В):
г азоту при температурі (В): 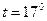 С була виконана робота
С була виконана робота  Дж. У скільки разів змінився тиск у 2,72 рази
Дж. У скільки разів змінився тиск у 2,72 рази
азоту при розширенні? зменшився .
Задача 5.6.
При ізотермічному розширенні водню масою 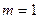 г, який мав температуру (В):
г, який мав температуру (В):  К, об’єм газу зріс у три рази. Визначити роботу
К, об’єм газу зріс у три рази. Визначити роботу 
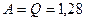 кДж
кДж
розширення газу і кількість теплоти  , яку одержав газ.
, яку одержав газ.
Задача 5.7.
При розширенні водень виконав роботу 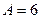 кДж. Визначити кількість теплоти (В):
кДж. Визначити кількість теплоти (В):
 , яка була надана газу, якщо процес відбувався: 1) ізобарно; 2) ізотермічно. 1) 21 кДж;
, яка була надана газу, якщо процес відбувався: 1) ізобарно; 2) ізотермічно. 1) 21 кДж;
2) 6 кДж.
Задача 5.8.
Водень за нормальних умов мав об’єм  м
м  . Визначити зміну
. Визначити зміну  (В): внутрішньої енергії газу при його адіабатному розширенні до об’єму 3,8 МДж.
(В): внутрішньої енергії газу при його адіабатному розширенні до об’єму 3,8 МДж.
 м
м  .
.
Задача 5.9.
Ідеальний газ виконує цикл Карно. Температура  охолоджувача дорівнює (В): 290 К. У скільки разів збільшиться ККД циклу, якщо температура нагрівача у 1,88
охолоджувача дорівнює (В): 290 К. У скільки разів збільшиться ККД циклу, якщо температура нагрівача у 1,88
підвищиться від  К до
К до  К.
К.
Задача 5.10.
Визначити зміну  ентропіі при перетворенні маси
ентропіі при перетворенні маси 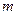 = 1 г льоду (
= 1 г льоду ( 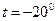 С) в (В): пару (
С) в (В): пару ( 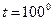 С).
С).  Дж/К.
Дж/К.
Задача 5.11.
Змішали воду масою 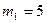 кг при температурі
кг при температурі  К з водою масою (В):
К з водою масою (В): 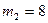 кг при температурі
кг при температурі  К. Визначити: 1) температуру суміші
К. Визначити: 1) температуру суміші  ;
;  =323 К;
=323 К;
2) зміну ентропії, яка відбулася при змішуванні. 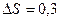 кДж.
кДж.
