Кинетические уравнения для населенностей уровней
Для анализа условий возникновения инверсной населенности в рассмотренных схемах оптической накачки составляются кинетические (балансные) уравнения, описывающие скорости изменения населенностей всех уровней в процессе накачки. Рассмотрим для примера трехуровневую схему накачки.
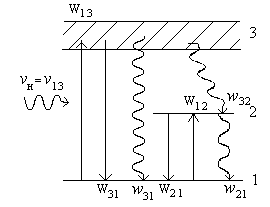 | Рис.1.14.Схема переходов в трехуровневой схеме оптической накачки. |
Вероятности для вынужденных переходов (Wij) и вероятности процессов релаксации (wij) на этом рисунке приведены с учетом особенностей оптического диапазона, для которого характерны большие расстояния между квантовыми уровнями (Еi-Ej>>kT). Скорости изменения населенностей квантовых уровней описываются следующими уравнениями:
DN3/dt=W13 (N1-N3)-w32N3-w31N3
DN2/dt=W21 (N1-N2) +w32N3-w21N2
DN1/dt =W21 (N2-N1) +W13 (N3-N1) +w21N2+w31N3 (1.64)
где учтено, что W12=W21, W13=W31= 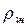 B13,
B13, 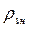 - спектральная объемная плотность энергии излучения накачки. Для определения порогового уровня накаfreакуимс нра5 ччки, при котором достигается инверсия населенностей между вторым и первым уровнями, т.е. N2>N1, достаточно проанализировать случай, когда под действием сильного излучения накачки установится стационарный режим, характеризирующийся условием dNi / dt=0.
- спектральная объемная плотность энергии излучения накачки. Для определения порогового уровня накаfreакуимс нра5 ччки, при котором достигается инверсия населенностей между вторым и первым уровнями, т.е. N2>N1, достаточно проанализировать случай, когда под действием сильного излучения накачки установится стационарный режим, характеризирующийся условием dNi / dt=0.
Тогда система(1.64) сводится к виду:
W13 (N1-N3)-w32N3-w31N3=0
W21 (N1-N2) +w32N3-w21N2=0
N1+N2+N3=N0 (1.65)
В этой алгебраической системе уравнений третье уравнение системы (1.64) заменено уравнением, определяющим полную населенность N0 в рассматриваемой системе.
Дальнейшее упрощение полученной системы связано с тем обстоятельством, что при dN3/dt=0 накопления частиц на третьем уровне не происходит, поэтому остается справедливым условие N3<<N1. Тогда система(1.65) приводится к виду:
W13N1-N3(w32+w31)=0
W21 (N1-N2) +N3w32-N2w21=0
N0 ≈N1+N2 (1.66)
Из этой системы находятся N1 и N2, а затем величина ∆= N2- N1, определяющая инверсию населенностей между вторым и первым уровнями: 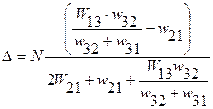 (1.67)
(1.67)
Возможность инверсного заселения второго уровня, используя механизм накачки через третий уровень, определяется выполнением физического условия, при котором вероятность релаксации с третьего уровня на второй должна быть значительно больше вероятности релаксации с третьего уровня обратно на первый, т.е. w32>>w31.
При этом w32=w32би+w32изл=w32би+A32 (1.68)
гдеw32би-вероятность безызлучательных переходов, а w32изл=А32 - вероятность спонтанных переходов. В рассматриваемой схеме должно выполняться условие w32изл≈0, т.е. w32≈w32би (вероятность релаксации 3→2 должна быть в основном безызлучательной).
Для перехода 2→1 наоборот основную роль должны играть излучательные переходы, т.е. w21 = w21би+A21≈ A21
C учетом сказанного, формула (1.68) принимает вид:
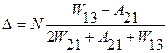 (1.69)
(1.69)
Отсюда ∆=(N2-N1)>0, если W13>A21=1/τ21сп (1.70)
Так как W13= 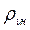 B13, то условие (1.70) можно представить в виде, которое определяет пороговый уровень накачки для достижения состояния с инверсией населенностей:
B13, то условие (1.70) можно представить в виде, которое определяет пороговый уровень накачки для достижения состояния с инверсией населенностей: 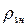 пор≥
пор≥ 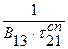 (1.71)
(1.71)
На рис.1.15. представлены графики изменения населенностей в трехуровневой (а) и четырехуровневой (б) схемах в зависимости от уровня накачки. Заштрихованные области соответствуют состоянию с инверсией населенностей квантовых уровней.
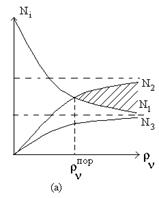 | 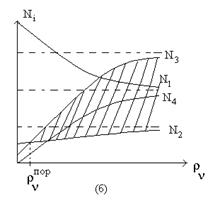 |
Рис. 1.15. Графики изменения населенностей.
Оптические резонаторы
В качестве колебательной системы в генераторах радиодиапазона применяется колебательный контур, а в СВЧ диапазоне - объемные резонаторы, представляющие собой отрезки пустого металлического волновода прямоугольной или цилиндрической формы. При этом размеры для объемного резонатора L порядка длины волны 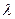 .
.
При дальнейшем увеличении частоты и переходе в миллиметровый или оптический диапазон изготовление объемных резонаторов столь малых размеров становится технологически невозможным. Кроме того, с уменьшением линейных размеров резко падает добротность резонатора.
Поэтому для инфракрасного и оптического диапазона вместо объемного резонатора А.М. Прохоровым был предложен открытый резонатор, представляющий собой систему из двух зеркальных поверхностей, установленных на расстоянии L друг от друга. В такой системе L>> 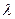 , что решает проблему реализации колебательной системы в оптическом диапазоне волн.
, что решает проблему реализации колебательной системы в оптическом диапазоне волн.
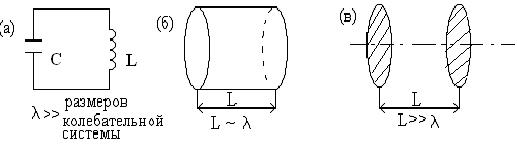
Рис.1.16.Колебательные системы для радио (а), СВЧ (б) и оптического диапазона волн (в).
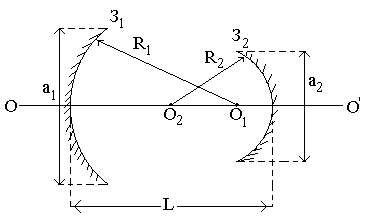
В общем случае открытый резонатор (ОР) представляет собой систему из двух зеркальных поверхностей сферической формы (рис.1.17.), характеризующийся следующими основными параметрами:1)Радиусы кривизны зеркал R1 и R2 с центрами в точках О1 и О2, расположенных на оптической оси ОО’; 2)База резонатора L; 3)Коэффициенты отражения зеркал по интенсивности r1 и r2; 4) g-параметры g1=1-L/R1, g2=1-L/R2
| Рис.1.17. Оптическая схема резонатора. |
 5)Число Френеля Nф= а1а2/λL, где а1 и а2 диаметры зеркал.
5)Число Френеля Nф= а1а2/λL, где а1 и а2 диаметры зеркал.
Рассмотрим в общем виде картину физических процессов при распространении электромагнитной волны в пассивном открытом резонаторе, содержащим между зеркалами однородную, изотропную и пассивную диэлектрическую среду.
При построении теории ОР определяющим являются дифракционные потери, связанные с дифракцией электромагнитного поля на краях зеркал, имеющих конечные размеры. Количественно дифракционные потери оцениваются числом Френеля Nф, определяющим число зон Френеля, укладывающихся на поверхности одного из зеркал, если смотреть из центра другого.
При больших числах Френеля (Nф>>100) дифракционными потерями можно пренебречь и использовать для анализа процессов в резонаторе метод геометрической оптики и простейшую волновую теорию.
В геометрическом приближении, пользуясь понятием светового луча, можно получить условие устойчивости открытого резонатора.
Волновая теория позволяет найти частотный спектр (собственные типы колебаний или продольные моды) открытого резонатора и получить первоначальное представление о распределении поля на поверхности зеркал.
Однако наиболее общей и полной является дифракционная теория ОР, в рамках которой можно получить информацию как о частотном спектре (продольные моды), так и пространственном распределении поля в поперечном направлении (поперечные моды).
