Примеры решения задач по электричеству и магнетизму
Задача 1. Два равных отрицательных заряда по 9 нКл находятся в воде на расстоянии 8 см друг от друга. Определить напряженность и потенциал поля в точке, расположенной на расстоянии 5 см от зарядов.
| Дано: | 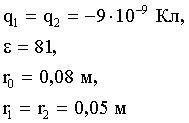 | 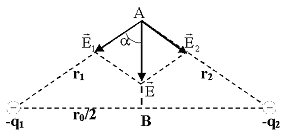 Рис.3 Рис.3 |
| Найти: | Е,φ |
Решение: Напряженность поля в точке А (рис. 3) по принципу суперпозиции равна:
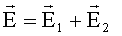
По теореме косинусов:
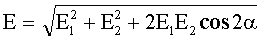
Напряженность поля точечного заряда:
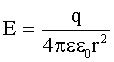
По условию 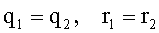 , следовательно,
, следовательно, 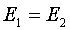 . Тогда:
. Тогда:

Но 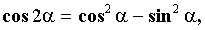 поэтому:
поэтому:
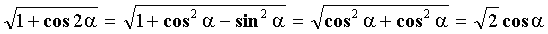
и результирующая напряженность равна:
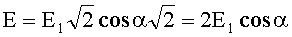
Обозначим АВ = h. Тогда 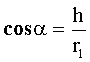
По теореме Пифагора:
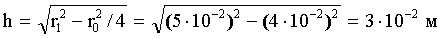
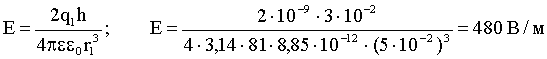
Потенциал φ результирующего поля в точке А равен:
Потенциал поля, создаваемого точечным зарядом, равен:
Но по условию  . Тогда
. Тогда 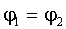 , следовательно:
, следовательно:
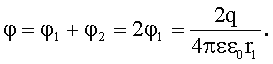
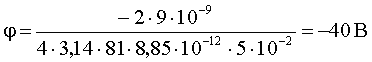
Проверка размерности:
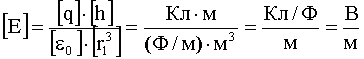
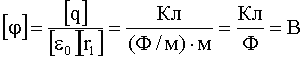
Ответ: Е = 480 В/м; φ = -40 В.
Задача 2. Электрон, ускоренный разностью потенциалов 6 кВ, влетает в однородное магнитное поле под углом 30º к направлению поля и начинает двигаться по спирали. Индукция магнитного поля равна В = 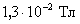 .
.
Найти радиус витка и шаг спирали.
| Дано: | 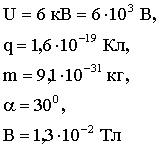 | 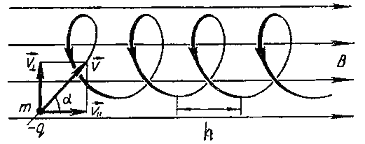 Рис.4 Рис.4 |
| Найти: | R, h. |
Решение: Скорость электрона найдем из условия, что работа сил электрического поля затрачивается на изменение кинетической энергии электрона:
А = ΔW. Работа в электрическом поле равна произведению заряда на разность потенциалов: А = qU. Начальная кинетическая энергия равна нулю, поэтому ΔW = W. Следовательно:
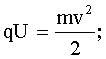 отсюда
отсюда 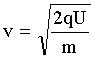 . (1)
. (1)
Разложим скорость электрона, влетающего в магнитное поле, на две составляющие: 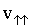 - составляющая скорости, направленная вдоль силовых линий поля и
- составляющая скорости, направленная вдоль силовых линий поля и 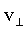 - составляющая скорости, направленная перпендикулярно силовым линиям поля. Из рис. 4:
- составляющая скорости, направленная перпендикулярно силовым линиям поля. Из рис. 4:

Проекция траектории электрона на плоскость, перпендикулярную к 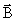 , представляет собой окружность, следовательно, сила Лоренца сообщает частице нормальное (центростремительное) ускорение. Сила Лоренца равна:
, представляет собой окружность, следовательно, сила Лоренца сообщает частице нормальное (центростремительное) ускорение. Сила Лоренца равна:
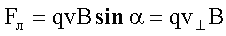
Центростремительное ускорение:
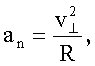
где R - радиус окружности.
По второму закону Ньютона: F = ma.
Тогда: 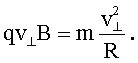
Отсюда: 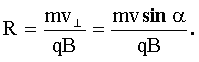 (2)
(2)
Период обращения равен:
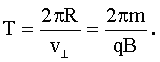
Так как скорость частицы имеет составляющую 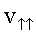 , то траектория частицы представляет собой винтовую линию.
, то траектория частицы представляет собой винтовую линию.
Шаг винтовой линии равен:
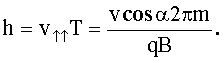 (3)
(3)
Проверка размерности расчетных формул (2) и (3).
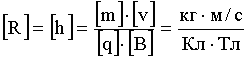
Размерность произведения [q]·[B] найдем из выражения для силы Лоренца:
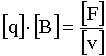
По второму закону Ньютона: F = ma, т.е.
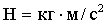
Тогда: 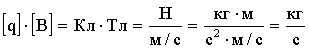
Следовательно, 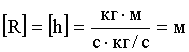
Подставим численные значения в (1), (2) и (3).
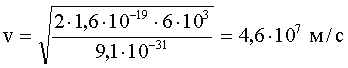
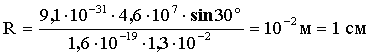
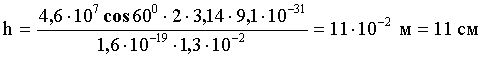
Ответ: R = 1 см, h = 11 см.
Задача 3. Проволочное кольцо радиусом 10 см лежит на столе. Какой заряд потечет по кольцу, если его повернуть с одной стороны на другую. Сопротивление кольца 1 Ом. Вертикальная составляющая индукции магнитного поля Земли равна 50 мТл.
| Дано: | 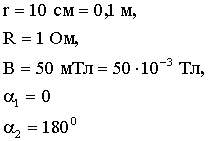 |
| Найти: | q |
Решение: По определению сила тока равна производной от заряда по времени:
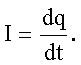
Отсюда заряд, который потечет по проводнику, определяется равенством:
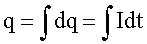 (1)
(1)
По закону Ома для замкнутой цепи сила тока равна:
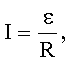 (2)
(2)
где ε - ЭДС источника, R - сопротивление цепи.
Ток в кольце появляется благодаря ЭДС индукции. Поэтому 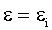 . ЭДС индукции найдем по закону Фарадея-Ленца:
. ЭДС индукции найдем по закону Фарадея-Ленца:
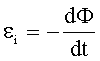 (3)
(3)
где 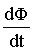 - скорость изменения магнитного потока.
- скорость изменения магнитного потока.
Подставим (3) в (2):
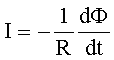 (4)
(4)
Подставим (4) в (1):
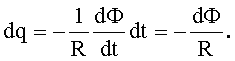 (5)
(5)
Проинтегрируем (5), получим:
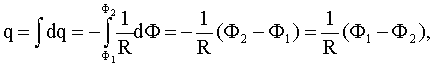
где 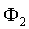 - магнитный поток, пронизывающий кольцо после поворота на угол180?;
- магнитный поток, пронизывающий кольцо после поворота на угол180?;
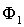 - магнитный поток до поворота.
- магнитный поток до поворота.
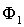 и
и 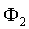 вычисляются по формулам:
вычисляются по формулам:

где В - индукция магнитного поля,
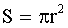 - площадь кольца,
- площадь кольца,
α - угол между нормалью к площади кольца и линиями индукции.
Тогда: 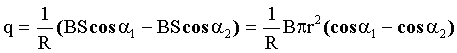
Проверка размерности:
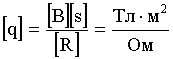
Так как 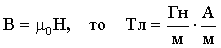
Размерность индуктивности найдем из закона 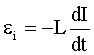
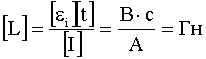
По закону Ома: 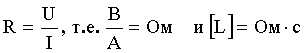
Тогда: 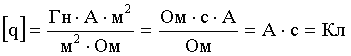
Вычислим q. Учтем, что до поворота нормаль к площади кольца параллельна вектору 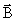 . Поэтому α1 = 0. После поворота нормаль противоположно направлена вектору
. Поэтому α1 = 0. После поворота нормаль противоположно направлена вектору 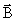 . Поэтому α2 = 180°. Тогда:
. Поэтому α2 = 180°. Тогда:
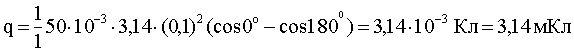
Ответ: q = 3,14 мКл.
Колебания. Волны
