Кінетичні наслідки з перетворень Лоренца.

Розглянемо коротко кінетичні (просторово-часові) наслідки з перетворень Лоренца (тобто, у кінцевому рахунку, з постулатів СТВ).

1) Обмеженість швидкості руху матеріальних об'єктів. З перетворень Лоренца (8.1) чи (8.2) видно, що при вони утрачають фізичний зміст, тому що при v=c координати і час приймають безсмислові нескінченні значення, а при вони взагалі стають мнимими, тобто нефізичними величинами. З цього випливає, що перетворення Лоренца мають фізичний сенс тільки при:

(9.1)

тобто відносна швидкість руху будь-яких ІСВ не може досягти швидкості світла у вакуумі. З огляду на те, що з кожною ІСВ реально зв'язане тіло відліку, що завжди є масивним (тобто має відмінну від нуля масу спокою), ми приходимо до важливого фізичного висновку: масивні матеріальні об'єкти ні в який ІСВ не можна розігнати до швидкості світла у вакуумі. До цього варто додати, що в Природі існують такі матеріальні об'єкти (наприклад, електромагнітні хвилі, фотони ) які у всіх ІСВ рухаються зі швидкістю світла у вакуумі відповідно до другого постулату СТВ (однак такі об'єкти не мають маси спокою, як ми переконаємося нижче, тому вони не можуть бути обрані як тіло відліку деякої ІСВ ). Таким чином, швидкість світла у вакуумі є гранична максимальна швидкість руху у всіх відомих матеріальних об'єктів.

Зауваження 1. В даний час фізики обговорюють гіпотезу про існування в Природі таких матеріальних об'єктів (їх називають тахіонами), швидкість руху яких у будь-яких ІСВ завжди , тобто, для яких швидкість світла у вакуумі є гранична мінімальна швидкість. Це гіпотеза не суперечить перетворенням Лоренца, тому що ці перетворення приводять тільки до висновку, що відомі матеріальні об'єкти не можна розігнати до швидкостей більше швидкості світла, тобто не можна перебороти "світловий бар'єр". Це, однак, не суперечить тому, що тахіони можуть існувати за "світловим бар'єром": тахіони, наприклад, можуть "народжуватися" у процесах взаємного перетворення мікрочастинок уже маючи швидкості, більші ніж "с" (ніякого подолання "світлового бар'єра" тут не відбувалося). Самий парадоксальний наслідок гіпотези існування тахіонов пов'язан з неминучим порушенням фізичного принципу причинності (див. про це нижче).

Зауваження 2.Швидкість "чого-небудь" може бути більше швидкості світла у вакуумі за умови, що це "що-небудь" не є матеріальне тіло. Наприклад, швидкість взаємного видалення космічних кораблів, що летять у протилежні сторони, обмірювана земним спостерігачем, може бути більше "с" (якщо стосовно Землі швидкість кожного корабля, наприклад, більше с/2), тому що тут мова йде про швидкість зміни відстані (тобто геометричної величини), а не про швидкість руху матеріального тіла. Але та ж сама швидкість, виміряна будь-яким космонавтом, буде менше "с" у відповідності з СТВ, тому що тут мова йде про швидкість руху матеріального тіла (корабля) у ІСВ, зв'язаної з іншим кораблем.

2) Відносність понять "одночасно", "раніш" і "пізніше" для двох подій. Принцип причинності в СТВ.

Нехай у системі 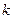відбулися дві події: перше – у момент у точці з координатами і друге – у момент у точці з координатами . Згідно (8.1) у системі ці події відбуваючись у момент часу:

,

Тому для проміжку часу між подіями в системі одержуємо вираз:

(9.2)

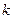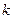З формули (9.2) випливає наступне: 1) якщо в системі ці події відбулися одночасно (тобто = ), але в різних точках простору (тобто ), то в системі маємо , тобто в цій системі події не будуть одночасними (за винятком часткового випадку "одномісних" подій, тобто коли ); 2) якщо в системі перша подія відбулася раніш другої (тобто < ), то згідно (9.2) для достатнього вилучених у просторі друг від друга подій ( ) одержуємо в системі результат , тобто в перша подія відбулася пізніше другої.

Таким чином, ми дійдемо висновку: у СТВ понять "одночасно", "раніш" і "пізніше" для двох подій відносні, тобто залежать від вибору ІСВ.

У зв'язку з цим виникає питання: чи не порушується при цьому принцип причинності, відповідно до якого подія - наслідок повинні завжди відбуватися пізніше події - причини (для двох подій, зв'язаних причинно - слідчим зв'язком)?

Для відповіді на це питання припустимо що формула (9.2) стосується до подій, зв'язаних причинно – слідчим зв'язком: нехай перша подія є причинною другої, тоді перша подія повинна зробити деякий фізичний (енергетичний) вплив, із-за якого відбудеться друга подія в точці . Але такий вплив може передатися тільки за допомогою деякого матеріального об'єкта (часток, полів і так далі), що (згідно 1) наслідку) не може рухатися швидше світла у вакуумі, тобто швидкість його . 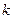Тоді в системі маємо (у припущенні сталості v) і формула (9.2) конкретизується так

(9.3)

Тому що згідно (9.1) V<c те , тому з (9.3) випливає, що при > і , тобто в системі часовий порядок наслідку цих подій не змінюється. Так як, принцип причинності в СТВ не порушується; цей принцип також підкоряється ПВЕ. Тому, зроблений вище висновок можна уточнити в таким чином: для двох подій, не зв'язаних між собою причинно - слідчим зв'язком, поняття "одночасно", "раніш" і "пізніше" будуть відносними; для подій же, зв'язаних причинно-наслідковим зв'язком, поняття "раніш" і "пізніше" маютьабсолютнийхарактер ( тобтоне залежатьвід вибору ІСВ ).

3)Уповільнення часу в ІСВ що рухається.

Нехай у системі в деякій фіксованій точці протікає деякий точковий фізичний процес, і нехай – момент початку цього процесу, а – момент його закінчення (ці моменти часу обмірювані годинником, нерухомим щодо точки, де відбувається процес). Час протікання (тривалість) процесу , обмірюваний нерухомим щодо процесу годинником, назвемо власним часом процесу. Тривалість цього процесу в системі 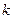позначимо через і назвемо координатним часом процесу (цей проміжок часу виміряється годинником, що рухається щодо процесу). Користаючись останнім співвідношенням з "зворотних" перетворень Лоренца (8.2), знаходимо зв'язокміж власним і координатним часом протікання процесу:

(9.4)

З цієї формули випливає, що проміжок (інтервал) часу є відносне поняття (що залежить від вибору ІСВ), причому , тобто тривалість процесу має найменше значення в тієї ІСВ, що нерухома (покоїться) відносно (точки), де цей процес відбувається (коротко: власний час процесу менше його координатного часу).

Отриманий результат можна переформулювати в інших термінах. Нехай ми знаходимося в системі k (яку умовно ми вважаємо нерухомою) і спостерігаємо за годинником системи , що рухаються щодо нас зі швидкістю V. Якщо годинник відраховує інтервал часу, наприклад , то згідно (9.4) годинник 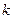(наш годинник) відраховують інтервал часу , тобто більший проміжок часу. А це означає, що годинник, що рухаються щодо нас, йдуть повільніше в порівнянні з нашими годинником. Іншими словами, у ІСВ що рухаються час сповільнюється стосовно умовно нерухомого ІСВ. Тому годинник системи йдуть повільніше по відношенню годин системи 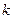, а по відношенню системи повільніше йдуть годинник системи 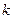, так вони рухаються в системі . І тут немає ніякого протиріччя, тому що в різних ІСВ годинник знаходяться в неоднакових станах руху. Залежність тимчасових характеристик (наприклад, тривалості) від стану руху фізичних об'єктів підтверджена експериментально з високою точністю (наприклад, час життя мюонів залежить від стану їхнього руху і відповідні виміри цілком підтверджують формулу (9.4))

4) Скорочення довжини тіла, що рухається, у напрямку його руху.

Розглянемо нерухомий щодо системи стрижень, розташований уздовж осі О^/Х^/. Стосовно системи 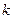цей стрижень рухається зі швидкістю V разом із системою . Позначимо довжину нерухомого стрижня (тобто довжину, обмірювану в системі ) через де і - координати початку і кінця стрижня в системі .

Довжину стрижня, що рухається, (тобто довжину, обмірювану в системі 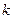) позначимо через , де і координати початку і кінця стрижня в системі 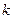, зафіксовані в той самий момент часу t (без одночасної фіксації початку і кінця довжину стрижня, що рухається, визначити неможливо). Відповідно до перетворень Лоренца (8.1), ці координати зв'язані співвідношеннями:

які дозволяють установити між l і l₀ наступний зв'язок:

(9.5)

З (9.5) видно, що l < l₀, тобто довжина тіла, що рухається, скорочується в напрямку його руху стосовно довжини того ж тіла, коли воно покоїться. Таким чином, поняття "довжина" (а разом з ним і поняття "об'єм") тіла є поняття відносне (залежне від вибору ІСВ). Формула (9.5) добре підтверджена відповідними експериментами.

5) Закон додавання швидкостей у СТВ.

Розглянемо рух матеріальної точки з погляду с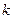истем і . Миттєву швидкість точки в системі 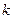позначимо через , а в системі - через .

Відповідно, для декартових компонент цих швидкостей маємо позначення:

(9.6)

Взявши тепер диференціали від лівих і правих частин перетворень Лоренца (8.2), одержуємо:

, , , (9.7)

Розділивши перші три співвідношення (9.7) на останнє, і маючи в увазі (9.6) одержимо закон додавання швидкостей:

(9.8)

В окремому випадку, коли матеріальна точка рухається уздовж осі O^/X^/ зі швидкістю в , з формул (9.8) одержимо:

(9.9)

При виконується (з непоганим ступенем точності) класичний закон додавання швидкостей (див. частина I, гл. 1, §5). Застосовуючи (9.9) до руху світла у вакуумі, тобто, вважаючи що з (9.9) одержуємо v=c , що погоджується (як і слідувало очікувати) з відповідним постулатом СТВ.

6) Абсолютні кінематичні величини в СТВ.

У СТВ, як ми переконалися вище, багато кінематичних (просторово-часових) величин (такі, наприклад, як відстань між точками , інтервал часу між двома подіями ) які є відносними (залежать від вибору ІСВ). Однак, у СТВ найважливіших значень мають і абсолютні (незалежні від вибору ІСВ) величини. Так, усвідомлення абсолютного характеру швидкості світла у вакуумі з'явилося "наріжним каменем" при побудові СТВ і склало зміст одного з вихідних її постулатів (принципів). Наслідком абсолютності швидкості світла у вакуумі є те, що в СТВ мається специфічна функція координат і часу,що також є абсолютною (тобто залишається незмінною при переході від однієї ІСВ до іншої).

Переходячи до побудови цієї функції, розглянемо дві довільні події, координати і час яких позначимо через і в системі 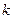й і в системі . У системах і 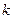складемо тепер функцію S₁₂ (відповідно S^/₁₂), квадрат якої визначимо в такий спосіб:

(9.10)

(9.11)

В окремому випадку, коли (тобто коли одне з подій відбувається в момент часу t = 0 на початку координат), позначаємо , , , , і записуємо (9.10) у вигляді:

(9.10^/)

Величина S₁₂ чи S називається просторово-часовим інтервалом. Її значення в СТВ визначається тим, що це є абсолютна величина. Дійсно, безпосереднім обчисленням за допомогою перетворень Лоренца можна переконатися в справедливості рівності:

(9.12)

яке є математичним записом інваріантості просторово-тимчасового інтервалу щодо перетворень Лоренца.

Записуючи квадрат інтервалу між двом нескінченно близькими подіям (ці події розділені нескінченними-малими проміжками часу dt і відстанню ) у вигляді:

(9.13)

виражаємо абсолютність dS рівністю:

чи (9.14)

Завдяки тому, що інтервал є інваріантна (абсолютна) величина, усі можливі інтервали між різними можливими подіями можна розділити також інваріантним образом на три класи (типу):

1) часоподібні інтервали, для яких виконується умова : у цьому випадку і події, що з'єднують цей інтервал, узагалі кажучи, можуть бути зв'язані між собою причинно-наслідковим зв'язком;

2) просторовоподібні інтервали, для яких виконується умова : у цьому випадку і тому одна подія не може бути причиною іншої, оскільки будь-який фізичний сигнал рухається зі швидкістю, що не перевищує швидкість світла, і не може зв'язати ці події;

3) нульові інтервали, для яких виконується умова : у цьому випадку і події можуть бути зв'язані причинно-наслідковим зв'язком, але тільки за допомогою світлових сигналів (чи таких сигналів, швидкість яких дорівнює швидкості світла у вакуумі, наприклад, гравітаційних).

З просторово-тимчасовим інтервалом зв'язана ще одна важлива абсолютна (інваріантна) величина - власний час процесу Dt. Повертаючись до позначень наслідку 3), обчислюємо квадрат інтервалу для процесу в системі , щодо якої процес протікає в одній точці (тобто ): маємо . Далі, користаючись рівністю (9.12), для інтервалу S₁₂ у системі маємо: , звідкіля випливає співвідношення між Dt і S₁₂ вигляду:

(9.15)

Так як праворуч у формулі (9.15) стоять абсолютні (інваріантні) величини, то власний час Dt є також абсолютна величина. Це, з іншого боку, ясно з операційного визначення власного часу процесу: Dt завжди виміряєтьсягодинником що покоїтьсящодо процесу, тому для всіх інших інерціальних спостерігачів є величини задана цим виміром.

Відзначимо тут для подальших посилань, що нескінченний-малий власний час dt зв'язано з координатним часом dt формулою:

(9.16)

де - миттєва швидкість тіла, що рухається з довільною змінною швидкістю . У зв'язку з формулою (9.16) необхідно пам'ятати, що вона справедлива для обчислення тільки нескінченно малих проміжків dt власного часу, так як тільки протягом нескінченно малого координатного часу dt можна зв'язати з тілом що нерівномірно рухається інерціальну систему . Для обчислення кінцевих проміжків власного часу процесів, зв'язаних з нерівномірно рухаючимся тілом, можна скористатися формулою:

(9.17)

яка одержується інтегруванням (9.16). Формулу ж (9.4) можна використовуватися тільки у випадку тіл що рівномірно рухаються, коли v=V=const

Формула (9.16) легко виводиться зі співвідношенням:

(9.18)

яке є аналог (9.15) для нескінченно малих dt і dS. Дійсно, згідно (9.18) маємо:

тобто формула (9.16) доведена.

На цьому ми закінчуємо виклад основних кінематичних наслідків з перетворення Лоренца. Подальший розвиток СТВ зв'язано з удосконаленням її математичного апарата.

§ 10. 4-мірний простір-час Минковского.

У попередніх параграфах ми коротко розглянули ті глибокі (корінні) зміни уявлень про фізичні властивості простору і часу, що досягнуті в рамках СТВ. Головне тут полягає у тому, що СТВ дозволяє усвідомити що:

1) мається глибокий зв'язок між властивостями простору і часу;

2) метричні властивості (такі як проміжки часу, лінійні розміри фізичних об'єктів) простору і часу в загальному випадку є відносними, тобто залежать від вибору ІСВ;

3) існують також просторово-часові характеристики (просторово-часовий інтервал, власний час, швидкість світла у вакуумі) фізичних процесів, що є абсолютними, тобто не залежать від вибору ІСВ.

Усі ці нові фізичні результати були сформульовані математичною мовою 3-мірного евклідового простору і 1-мірного часу, тобто з використання двох різних математичних просторів, ніяк спочатку (тобто до фізичної інтерпретації їх) між собою не зв'язаних. Це, однак, суперечить (не відповідає) самої суті отриманих фізичних результатів, перерахованих вище. Тому, усвідомивши зазначену невідповідність між фізичними властивостями П и Ч і використовуваним при цьому "3-мірним" математичним апаратом, австрійський фізик Герман Минковский у 1908 році поставив своєю метою розробити адекватний фізичним результатам СТВ математичний апарат. Для цього він ввів у розгляд 4-мірний математичний простір, декартові координати якого зв'язані взаємно однозначно з декартовими координатами x, y, z і часом t фізичної події наступними співвідношеннями:

(10.1)

де с – швидкість світла у вакуумі. Чотиривимірний простір, що поєднує фізичний тривимірний простір і час, називається простором-часом Минковского (П-Ч Минковского). Точки П-Ч Минковского називаються світовими точками, а лінії в ньому - світовими лініями. З (10.1) видно, що існує взаємно однозначна відповідність між світовими точками і подіями. Набір чисел (10.1) можна вважати декартовими координатами кінця 4-х-радіуса-вектора ; тут і нижче чотиривимірні вектора, тобто вектора П-Ч Минковского ми будемо позначати стрілкою внизу (наприклад , ). Геометричні (метричні) властивості П-Ч Минковского визначаються (постулюються) тим, що відстань між двома світовими точками визначається просторово-тимчасовим інтервалом (9.10): наприклад, для квадрата довжини чотиривимірного радіуса-вектора постулюється вираження квадрата інтервалу (9.10^/), тобто в позначеннях (10.1) визначаємо:

(10,2)

де - так називаний метричний тензор П-Ч Минковского, який визначений у такий спосіб:

(10.3)

П-Ч Минковского, у якому відстань визначена формулою (10.2) – (10.3), називається псевдоевклідовим простором (він був б евклідовим, якби замість (10.3) був = , де - чотиривимірний символ Кронекера), а система декартових координат у ньому називається евклідовою системою координат. З визначення (10.3) видно, що метричний тензор можна записати у формі матриці :

(10.3^/)

де перший індекс m нумерує рядки, а другий індекс n - стовпці матриці.

Так як S² і, отже, R² є інваріант перетворень Лоренца, те геометрично перетворення Лоренца (8.1) можна представити як перетворення координат П-Ч Минковского при поворотах евклідової системи координат у цьому просторі (у силу того, що при таких поворотах довжина 4-радіуса-вектора не змінюється). Дійсно, у позначеннях (10.1) перетворення Лоренца (8.1) записуються у вигляді:

(10.4)

Представляючи координати матеріальної точки у вигляді матриць з одним стовпцем:

(10.5)

можна переписати (10.4) у матричному вигляді:

, (10.4^/)

де - матриця Лоренца (індекс m нумерує її рядка, а індекс n - її стовпці), явний вид якої, згідно (10.4):

(10.6)

Матриця є псевдоортогональною матрицею, що описує поворот евклідової системи координат у площині . Таким чином, (10.4) є геометрична інтерпретація перетворень Лоренца (8.1) у вигляді перетворень координат матеріальніх точок у П-Ч Минковского при поворотах евклідової системи координат.

Геометрія П-Ч Минковского лежить в основі сучасного математичного апарата СТВ. У П-Ч Минковского можна розвити тензорну алгебру і тензорний аналіз. Ми приведемо тут деякі поняття 4-мірної тензорної алгебри, необхідні для подальшого розвитку СТВ.

4-скаляром у П-Ч Минковского називається така функція координат , що інваріантна щодо перетворень координат (10,4^/), тобто щодо перетворень Лоренца (8.1): . Прикладом 4-скалярів може бути: інтервал , власний час , швидкість світла у вакуумі з ( с - це постійний4-скаляр).

4-вектором уП-Ч Минковского називається набір чотирьох функцій , що при перетворенні координат (10.4^/) перетворяться так само, як і координати, тобто за правилом:

, (10.7)

Квадрат довжини 4-вектора визначається за аналогією з (10.2) :

(10.8)

Для зручності запису формул можна ввести інший "клас" компонентів чотирьох вектора , що позначаються індексом унизу (А_m) і визначаються через компоненти А^m за правилом:

(10.9)

Величини А^m називатися контраваріантними компонентами чотирьохвектора , а А_m - коваріантними компонентами чотирьохвектора . Використовуючи (10.9), квадрат 4-вектора (10.8) можна записати у вигляді:

(10.10)

За аналогією з (10.8) і (10.10) визначається скалярний добутокдвох чотирьохвекторів і :

(10.11)

З (10.3),(10.9),(10.11) видно, що "опускати" і "піднімати" індекси (тобто переходити від контраваріантних компонентів до коваріантного і навпаки) можна за допомогою метричного тензора по формулах:

(10.12)

якщо визначити контраваріантні компоненти метричного тензора так:

, (10.13)

Стосовно чисто просторових поворотів системи координат (не торкаються вісь часу ) три компоненти чотирьохвектора утворять тривимірний вектор , а тимчасовий компонент являє собою тривимірний скаляр. Тому, при перерахуванні компонентів ми будемо часто писати так:

(10.14)

де ми взяли до уваги (10.9). Відповідно, для квадрата чотирьохвектора (10.10) можна використовувати запис:

(10.15)

Наприклад, для компонента ; - радіуса-вектора можна писати:

(10.16)

де 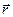– тривимірний радіус-вектор точки.

Далі, чотирьохтензором другого рангу називається сукупність 16 величин , що при перетвореннях координат (10.4^/) перетворяться як добутки компонентів двох чотирьохвекторов і , тобто за правилом:

, (10.17)

Виражаючи більш точно, є контраваріантні компоненти 4- тензора другого ранта. Можна також використовувати його змішані ( ) і коваріантні ( )компоненти , які можна одержати з послідовним "опусканням" індексів (див.(10.12)):

(10.18)

Звідси, приймаючи в увагу (10.3), маємо:

;

Стосовно чисто просторових поворотів компонента де утворять 3-мірний тензор другого рангу, компоненти і – це компонента тривимірних векторів і – тривимірний скаляр.

Тензор називається симетричним, якщо , і антисиметричним,якщо (діагональні компоненти антисиметричного тензора дорівнюють нулю; цей тензор має всього шість незалежних компонентів).

З компонентів тензора можна утворювати скаляр, якщо взяти наступну суму (див.(10.18)):

(10.19)

Ця сума називається слідом тензора а операція, за допомогою якої вона отримана, називається спрощенням тензора. Узагалі, спростити тензор

довільного рангу по індексах, α і μ наприклад, це значить – узяти суму ; у результаті виходить тензор, ранг якого на дві одиниці менше (спрощувати можна тільки по індексах, один із яких – верхній, а другий нижній).

Одиничним; 4-тензором називається тензор , що має властивість:

, (10.20)

де - довільний 4-вектор. З (10.20) видно, що:

(10.21)

отже .

На цьому тут ми обмежимося у викладі математичного апарата

П-Ч Минковского і приведемо кілька фізичних прикладів 4-векторів.

Чотирьохвектор швидкості (по аналоги з 3-вектором швидкості ) визначається так:

(10.22)

де . З (10.22) видно, що компоненти 4-швидкості є:

(10.23)

Компоненти 4-швидкості (на відміну від компонентів 3-швидкості) між собою залежні, тому що задовольняють додатковій умові:

, (10.24)

у справедливості якого легко переконатися або безпосереднім обчисленням, або розділивши на вираження для квадрата інтервалу. Співвідношення (10.24) означає, що квадрат чотирьохшвидкості є постійний чотирьохскаляр, тобто величина, однакова у всіх ІСВ.

Чотирьохвектор прискорення (за аналогією зі звичайним трьохвектором прискорення) визначається співвідношенням

(10.25)

Диференціюючи за власним часом ліву і праву частини співвідношення (10.24), одержуємо:

(10.26)

відкіля видно, що чотирьохвектор швидкості і чотирьохвектор прискорення перпендикулярні один одному в П-Ч Минковского.

Інші приклади чотирьохвекторів і чотирьохтензорів у П-Ч Минковского ми приведемо в наступних параграфах.

На закінчення цього параграфа зробимо одне дуже важливе зауваження, що переконливо демонструє переваги використання математичного апарата 4-мірного П-Ч Минковского при пошуку нових фізичних законів, що задовольняють принципам СТВ.

Представляючи фізичні величини у виді чотирьохвекторів П-Ч Минковского визначеного рангу, запишемо деякий фізичний закон у чотиривимірній формі:

, (10.27)

тобто у вигляді рівності двох чотирьох тензорів однаковогорангу з однаковим числом контраваріантних і коваріантних індексів. При поворотах евклідової системи координат у П-Ч Минковского (тобто, при переході від однієї ІСВ до іншої за допомогою перетворень Лоренца) ліва і права частини (10.27) будуть перетворюватися однаково, тобто вид рівняння (10.27) буде однаковим у всіх ІСВ. Таким чином, закони фізики, що записані в чотиривимірній формі (10.27), є релятивістськи інваріантними. Для перевірки релятивістської інваріантості законів фізики, записаних у тривимірній формі (наприклад, рівнянь Максвела), досить спробувати представити їх у чотиривимірній формі (10.27).

§11. Релятивістська динаміка.

Для знаходження рівняння руху матеріальної точки, на яку діє сила (основного закону динаміки СТВ), необхідно:

1) шукати (постулювати) його в чотиривимірній формі (див. зауваження наприкінці §10);

2) задовольняти при цьому принципу відповідності з динамікою Ньютона, тобто при з чотиривимірного закону динаміки повинний випливати другий закон Ньютона:

, (11.1)

Тому ми повинні попередньо визначити чотирьохвектор імпульсу і чотирьохвектор сили як природне 4-мірне узагальнення векторів і .

Чотирьохвектор імпульсу р^m визначений формулою:

, , (11.2)

де m₀ – так називана маса спокою (тобто маса матеріальної точки що покоїться). Компоненти р^m мають вигляд:

(11.3)

Тривимірний вектор:

(11.4)

називається релятивістським імпульсом. З (11.4) видно, що (як і нерелятивістський імпульс ) його можна представити як величину, пропорційну швидкості, якщо масу m матеріальної точки, що рухається, визначити співвідношенням:

(11.5)

тобто маса частки (тіла) росте зі збільшенням її швидкості. Це означає, що СТВ маса m залежить від вибору ІСВ, тобто не є абсолютною величиною (на противагу класичній механіці, де , тобто маса не залежить від вибору ІСВ). При малих швидкостях ( ) вираз (11.4) для релятивістського імпульсу переходить у визначення нерелятивістського імпульсу.

Вводячи тепер для чотирьохвектора сили (сили Минковского)позначення , постулюємо шуканий основний закон динаміки СТВ (4-мірне рівняння руху) у вигляді:

(11.6)

У компонентному вигляді ці чотири рівняння можна записати так:

(11.7)

(11.8)

З'ясуємо тепер зв'язок з звичайним вектором сили . Для цього перепишемо (11.8) у вигляді (з огляду на, що ):

(11.8^/)

Щоб задовольнити принципу відповідності з рівнянням (11.1) ми повинні прирівняти праву частину (11.8^/) вектору , тобто покласти:

(11.9)

Таким чином, вектор зв'язаний зі звичайною силою співвідношенням (11.9), тому (11.8) можна записати у вигляді:

(11.8^//)

де дається вираженням (11.4). Рівняння (11.8^//) є релятивістська форма запису другого закону Ньютона: це рівняння коректно описує динаміку релятивістської (тобто, що рухається з будь-якими швидкостями в інтервалі ) матеріальної точки в заданій ІСВ. Це рівняння тривимірне, тому неінваріантне щодо перетворень Лоренца.

Далі, підставляючи (11.2) у (11.6), перепишемо основний закон руху динаміки СТВ у вигляді:

(11.6^/)

де - чотирьохвектор прискорення (10, …)...Підставляючи (11.6^/) у співвідношення (10, …), маємо:

,

звідкіля, з огляду на (10,…)і (11.9), одержуємо для компонента вираз:

, (11.10)

тобто компонент зв'язаний з механічною потужністю (роботою в одиницю часу). Таким чином, вираз (11.9) і (11.10) дозволяє записати компоненти сили Минковского у вигляді:

(11.11)

З'ясувавши фізичний зміст компонентів чотирьохвектора сили і рівняння (11.8), перейдемо до з'ясування фізичного змісту рівняння (11.7). Приймаючи до уваги формули (11.3) і (11.10), перепишемо (11.7) у вигляді:

(11.7^/)

Так праворуч у (11.7^/) стоїть вираз для роботи в одиницю часу, що виконує сила , тобто ґрунтуючись на законі збереження і перетворення енергії (який виконується в СТВ в силу однорідності часу), ми можемо стверджувати, що ліворуч у рівності (11.7^/) стоїть вираз для зміни енергії матеріальної точки в одиницю часу. Отже, у дужках у лівій частині (11.7^/) стоїть вираз для енергії матеріальної точки, визначений з точністю до довільної постійної (можна однак показати, що ця постійна повинна бути обрана рівної нулю – у протилежному випадку буде протиріччя з законом додавання швидкостей у СТВ). У такий спосіб величина:

(11.12)

визначає енергію матеріальної точки (тіла), що рухається зі швидкістю v. При v=0 з (11.12) одержуємо:

(11.13)

так звану енергію спокою матеріальної точки (тобто її внутрішню енергію). Таким чином, з масою завжди зв'язана енергія (і навпаки), тому в релятивістській механіці не існує окремо законів збереження маси й енергії – вони поєднанні в єдиний закон збереження повної (тобто, що включає енергію спокою) енергії частки. Наближений їхній поділ можливий лише в класичній фізиці, коли і не відбувається перетворення одних часток в інші: при з (11.12) маємо:

(11.14)

При енергія масивної частки, згідно (11.12) збільшується нескінченно. Тому, приймаючи до уваги закон збереження енергії, дійдемо висновку: прискорити масивне тіло до неможливо, тому що для цього треба була б нескінченна енергія, що, в принципі, не здійсненно. Зі швидкістю світла у вакуумі можуть рухатися тільки "безмасові" тіла, для яких m₀ = 0 (наприклад, фотони).

З врахуванням (11.12), компоненти чотирьохвектора імпульсу р^m (11.3) можна представити у вигляді:

(11.15)

Тому вираз для квадрата 4-вектора імпульсу можна переписати так:

(11.16)

Співвідношення між енергією і релятивістським імпульсом (11.6) широко використовується в сучасній фізиці (нагадаємо, що в класичній механіці відповідне співвідношення мало вигляд ). Для часток з нульовою масою спокою з (11.16) випливає:

( 11.17)

Для вільної матеріальної точки замість (11.6) маємо:

чи (11.18)

тобто збереження 4-вектора імпульсу, що згідно (11.15) означає одночасне збереження й енергії ( ) і релятивістського імпульсу ( ).

Зауваження. У цьому параграфі ми побудували релятивістську динаміку однієї матеріальної точки, що рухається в деякім силовому полі. Шляхом очевидних узагальнень легко побудувати динаміку системи, що складається з багатьох матеріальних точок за умови, що ці точки між собою не взаємодіють.Для таких систем їхні повні характеристики, такі як повна енергія системи Е, релятивістський імпульс системи, чотирьохвектор імпульсу системи р^m, є аддитивними величинами:

, , ,

Однак при врахуванні взаємодії між матеріальними точками ситуація різко ускладнюється, тому що всі перераховані величини втрачають властивості аддитивності. Це зв'язано c тією обставиною, що при утворенні з вільних часток стійкої системи взаємодіючих часток виділяється надлишок енергії (рівний енергії зв'язку) DЕ, якому згідно (11.12) відповідає маса . . Тому повна маса системи менше суми мас її часток, що утворяться, на величину (так званий дефектмас), і згадані властивості аддитивності губляться. Унаслідок цього проблема побудови релятивістської динаміки систем взаємодіючих часток виявляється дуже складною і відповідної теорії в даний час не існує (маються тільки деякі наближені результати для випадку слабкої взаємодії між класичними частками).

Розділ 3. Релятивістська інваріантість законів електродинаміки вакууму.

У цій главі ми переконаємося в релятивістській інваріантності законів електродинаміки для зарядів і струмів у вакуумі (рівняння для електромагнітних потенціалів і рівнянь Максвела). Для цього, як ми покажемо в §12, необхідно записати ці закони в чотиривимірній формі, тобто у вигляді тензорних рівнянь у П-Ч Минковского.

§12 Релятивістська інваріантна форма рівнянь для електромагнітних потенціалів.

У §6 ми довели, що при виборі калібрування Лоренца (6.4^/):

(12.1)

рівняння (6.9^//) - (6.10^//) для електромагнітних потенціалів і мають вигляд: (12.2)

(12.3)

де

(12.4)

є оператор Даламбера. Запишемо рівняння (12.1) - (12.3) у 4-мірній формі. Використовуючи чотиривимірні позначення, запишемо оператор Даламбера (12.4) у наступному вигляді (див. §10): (12.5)

,

звідки видно, що оператор Даламбера є чотиривимірний скалярний диференціальний оператор, що, відповідно до визначення чотирьохскалярів (10,…),є інваріантним перетворенням Лоренца, тобто має однаковий вигляд у всіх ІСВ ( ) і, отже, не змінює трансформаційних властивостей тих функцій, на які він діє (тобто після дії цього оператора скаляр залишається скаляром, вектор – вектором, тензор – тензором).

Далі, переписавши рівняння (12.2) у вигляді:

ми бачимо, що рівняння (12.2) – (12.3) можна об'єднати і записати в чотиривимірнім вигляді:

(12.6)

чи , ,