Описание установки и вывод расчетной формулы. Установка, с помощью которой определяют отношение теплоемкостей воздуха по методу адиабатического расширения (Клемана-Дезорма)

Установка, с помощью которой определяют отношение теплоемкостей воздуха по методу адиабатического расширения (Клемана-Дезорма), изображена на рисунке 1.

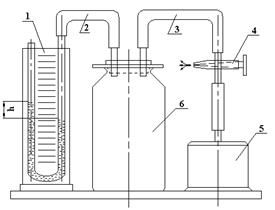
Рисунок 1 Схема лабораторной установки: 1 – манометр жидкостной; 2 и 3 - соединительные шланги; 4 – кран;

5- пневматический насос; 6 – баллон

Установка представляет собой баллон 6, соединенный трубкой 2 с водяным манометром 1. Кран 4 служит для соединения сосуда с насосом 5. С помощью насоса будем накачивать в сосуд воздух до тех пор, пока жидкость в правом колене манометра не достигнет некоторого значения шкалы.

При сжатии воздуха его температура сначала повысится, а через некоторое время, благодаря теплообмену с внешней средой, воздух в сосуде примет комнатную температуру. В период охлаждения воздуха в сосуде созданное там давление немного снизится и потом будет сохраняться неизменным (рисунок 2).

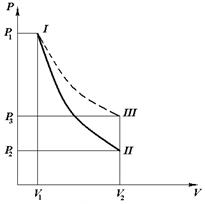
Рисунок 2 График процессов:

I – II адиабата; II-III изохора; I-III изотерма

При этом избыточное давление 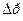, определяется по разности уровней жидкости 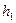, т.е. 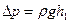. Абсолютная температура окружающего воздуха и воздуха в сосуде одинакова и равна 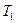. Полное давление в сосуде 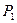равно сумме атмосферного 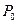и избыточного давлений, т. е.:

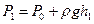. (5)

Два параметра 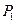и 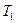характеризуют начальное состояние воздуха в сосуде, которое назовем первым состоянием (I-е состояние , ).

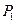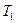Теперь откроем и быстро (через 1-2 с) закроем кран 4. За этот короткий промежуток времени воздух в сосуде будет расширяться адиабатически (без обмена теплом с окружающей средой), пока его давление не станет равным атмосферному, т. е. 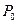. При адиабатическом расширении воздуха его температура понизится до некоторого значения 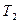. Следовательно, это состояние воздуха будет характеризоваться параметрам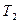и и 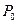(II-е состояние , ).

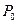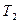После закрытия крана 4 имевшееся давление воздуха в сосуде 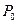будет повышаться, так как в результате теплообмена его температура будет возрастать до значения 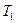, соответствующего температуре окружающего воздуха. Пусть при этом давление достигнет величины

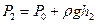, (6)

где 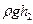— избыточное давление, показываемое манометром, Па.

Таким образом, третье состояние воздуха характеризуется параметрам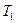и и (III-е состояние , ).

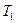Обозначим объем той массы воздуха, которая осталась в сосуде после удаления части воздуха (когда он был открыт), через 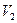. До открытия сосуда та же масса воздуха занимала меньший объем 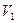. После открывания крана, когда установилась постоянная температура, также объем 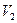. Сопоставляя первое и третье состояния, заметим, что температура воздуха одинаковая. Очевидно, здесь можно применить закон Бойля-Мариотта, т. е:

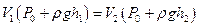
или

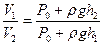. (7)

Сравнивая первое и второе состояния, отмечаем, что они имеют разные температуры, процесс расширения происходит адиабатически, т.е. здесь следует применить уравнение Пуассона:

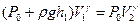. (8)

Отсюда находим

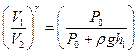. (9)

Возведем обе части равенства (7) в степень :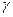

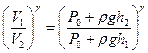. (10)

Сопоставив равенства (9) и (10), получим

.

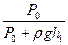
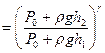После логарифмирования

.

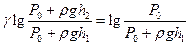Отсюда

.

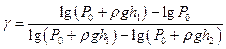Применяя математические преобразования, допустимые для приближенных вычислений, получим:

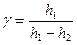. (11)

Таким образом, для определения отношения теплоемкостей 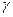достаточно на опыте измерить давления 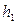и 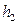.