Поле внутри плоской пластины

Рассмотрим поле, создаваемое в вакууме двумя бесконечными разноименно заряженными плоскостями. Обозначим напряженность поля 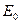, а электрическое смещение 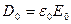. Внесем в это поле пластину из однородного диэлектрика. Под действием поля диэлектрик поляризуется и на его поверхностях появятся связанные заряды плотности 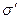. Эти заряды создадут внутри пластины однородное поле, напряженностью .

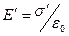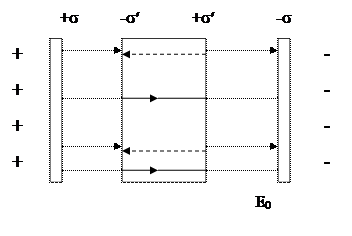
Рис. 14.4.

Вне диэлектрика в данном случае 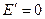. Напряженность поля 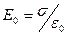. Оба поля направлены навстречу друг к другу, следовательно, внутри диэлектрика

.

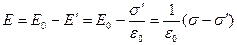Так как 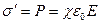, то получим

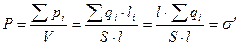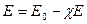, , откуда

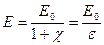, умножив на 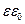, получаем электрическое смещение внутри пластины:

.

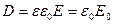Таким образом, внутри пластины электрическое смещение равно напряженности поля свободных зарядов, умноженной на 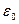, т.е. совпадает с электрическим смещением внешнего поля .

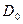Электроемкость

Сообщенный проводнику заряд q распределяется по его поверхности так, чтобы напряженность поля внутри проводника была равна нулю. Увеличение заряда приводит к увеличению напряженности поля в каждой точке окружающего проводник пространства. Следовательно, возрастет потенциал проводника. Таким образом, для уединенного проводника:

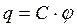. (14.16)

Коэффициент пропорциональности С между потенциалом и зарядом называется электроемкостью проводника. Из (14.16) следует, что:

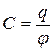. (14.17)

Электроемкость численно равна заряду, сообщение которого проводнику повышает его потенциал на единицу.

Вычислим потенциал заряженного шара радиуса R. Между разностью потенциалов и напряженностью поля существует соотношение:

.

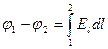Поэтому потенциал шара 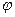можно найти, проинтегрировав выражение для напряженности вне сферы

,

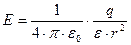по r от R до ¥ (потенциал на бесконечности полагаем равным нулю).

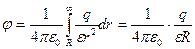. (14.18)

Сравнивая (14.18) с (14.17), находим, что емкость уединенного шара радиуса R, погруженного в однородный безграничный диэлектрик с относительной проницаемостью 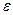, равна:

.

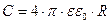За единицу емкости принимают емкость такого проводника, потенциал которого изменяется на 1В при сообщении ему заряда в 1К. Эта единица емкости называется фарадой (Ф). 1 Ф = .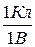

Конденсаторы

При поднесении к заряженному проводнику какого-либо тела потенциал проводника уменьшается по абсолютной величине, вследствие возникновения индуцированных (на проводнике) или связанных (на диэлектрике) зарядов. Согласно формуле (14.17) для емкости это означает увеличение емкости проводника. Это явление положено в основу устройств, называемых конденсаторами. Найдем формулу для емкости плоского конденсатора. Если площадь обкладки S, а заряд на ней q, то напряженность поля между обкладками равна:

.

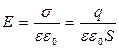Разность потенциалов между обкладками равна:

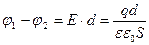, откуда для емкости плоского конденсатора получаем:

,

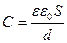где d – величина зазора между обкладками.

Энергия системы зарядов

Пусть имеются заряды q₁ и q₂, находящиеся на расстоянии r₁₂. Когда заряды удалены друг от друга на бесконечность, они не взаимодействуют. Положим в этом случае их энергию равной нулю. Сближение зарядов можно произвести приближая q₁ к q₂, либо наоборот. В обоих случаях совершается одинаковая работа. Работа переноса заряда q₁ из бесконечности в точку, удаленную от q₂ на r₁₂, равна:

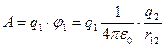, (14.19)

где 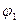- потенциал, создаваемый зарядом q₂ в той точке, в которую перемещается заряд q₁. Аналогично работа переноса заряда q₂ из бесконечности в точку, удаленную от q₁ на r₁₂, равна:

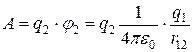, (14.20)

где 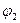- потенциал, создаваемый зарядом q₁ в той точке, в которую перемещается заряд q₂. Значения работ (14.19) и (14.20) одинаковы, и каждое из них выражает энергию системы:

.

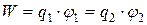Для того чтобы в выражении энергии системы оба заряда входили симметрично, напишем его следующим образом:

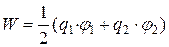. (14.21)

В случае N зарядов потенциальная энергия системы равна:

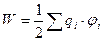, (14.22)

где 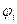- потенциал, создаваемый в той точке, где находится q_i, всеми зарядами, кроме i-го.