Мета роботи саме і полягає в якісній перевірці співвідношення (6) для фотонів
Лабораторна робота №5-12
З дисципліни: «Фізика»
На тему: «Дослідження співвідношення
невизначеностей Гейзенберга для фотонів»
Підготував: студент групи МІТ-11(б)
Сікорський Дмитро
Перевірили: к.ф.-м.н.,доц. Стасенко В.А.
пров.інж. Камінський О.С.
Вінниця 2012
Мета роботи:якісно експериментально перевірити справедливість співвідношень невизначеностей.
Прилади і матеріали:лазер ЛГН-105, щілина з мікрометричним гвинтом, екран, лінійка.

Теоретичні відомості
Спостереження, а також експериментальне і теоретичне дослідження дифракції, інтерференції, поляризації переконливо доводять хвильову природу світла. Однак закономірності ряду інших явищ, зокрема, фотоефекту, теплового випромінювання, ефекту Комптона можна пояснити, припустивши, що світло має корпускулярні властивості. Частинки світла, поняття про які ввів А.Ейнштейн (1905 p.), називаються фотонами. Таким чином, світло має одночасно як хвильові, так і корпускулярні властивості. Нові ідеї потрібні були і для розв'язання принципових труднощів класичної фізики при обґрунтовані стійкості атомів, лінійності спектрів випромінювання і поглинання. У цьому відношенні істинно революційною, як показав досвід створення квантової механіки, була гіпотеза Луї де Бройля (1924 p.), що мікрочастинки, поряд з корпускулярними, мають також хвильові властивості. Таким чином, матерія як у вигляді поля, так і у вигляді речовини має корпускулярні і хвильові властивості. У цій єдності полягає суть корпускулярно-хвильового дуалізму матерії. З корпускулярної точки зору динамічний стан частинки визначається її імпульсом р, в той час як хвильові властивості описуються довжиною хвилі λ. Єдність цих та інших властивостей виражається формулою де Бройля, яка пов'язує імпульс р ідовжину хвилі де Бройля λ :
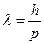 . (1)
. (1)
Корпускулярно-хвильовий дуалізм матерії накладає обмеження на можливість описування руху частинок за допомогою класичних понять, зокрема, понять траєкторії. Коли мова йде про траєкторію, припускається, що в довільний момент часу як завгодно точно одночасно визначені координати та імпульс частинки. Розглянемо з цієї точки зору вимірювання координати х частинки (наприклад, фотона), яка рухається з імпульсом р паралельно осі у. Длявизначення координати частинки перпендикулярно до осі у розташуємо діафрагму (щілину) шириною Δх і екран (рис. 1). Проходження частинки через щілину супроводжується появою свічення в якійсь точці екрана. Спостерігаючи свічення, можна стверджувати, що в момент проходження щілини координата частинки дорівнює х і визначена з похибкою ∆х. Для збільшення точності вимірювання потрібно зменшити ∆х. Якщо частинка має хвильові властивості, то при 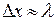 повинна спостерігатись дифракція. Розподіл дифракційних максимумів на екрані схематично показаний на рис.1. Корпускулярні властивості проявляються в тому, що частинка проходить через щілину і рухається до екрана як ціле, не розділяючись на будь-які частини.
повинна спостерігатись дифракція. Розподіл дифракційних максимумів на екрані схематично показаний на рис.1. Корпускулярні властивості проявляються в тому, що частинка проходить через щілину і рухається до екрана як ціле, не розділяючись на будь-які частини.
Хвильові властивості проявляються в тому, що частинка попадає переважно в ті точки екрана, для яких виконується умова максимуму для дифракції на щілині. Попадання частинки в точку екрана свідчить про те, що вона має складову Δpx, паралельну осі х. До щілини Δpx=0, тобто рх було відомо точно. Величина Δpx називається невизначеністю імпульсу. Оскільки кут φ, під яким частинка попадає в довільну точку екрана, що відповідає дифракційним максимумам вищих порядків, задовольняє умову
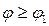 , (2)
, (2)
де φ1 визначає напрям на перший дифракційний мінімум, то як видно з рис.1:
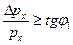 (3)
(3)
При малих кутах 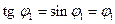 .Використовуючи умову спостереження першого дифракційного мінімуму
.Використовуючи умову спостереження першого дифракційного мінімуму
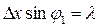 , (4)
, (4)
з формул (3) і (4) одержуємо:
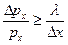 . (5)
. (5)
Виключивши з (1) і (5) довжину хвилі де Бройля λ, знаходимо:
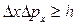 . (6)
. (6)
Нерівність (6) - співвідношення невизначеностей Гейзенберга. Згідно з співвідношенням (6) для як завгодно точного визначення координати і відповідної єдності корпускулярних і хвильових властивостей не існує точних значень спряжених координат і імпульсу. Отже, по суті співвідношення невизначеностей зводиться до неможливості описати рух частинок за допомогою поняття траєкторії.
Мета роботи саме і полягає в якісній перевірці співвідношення (6) для фотонів.
Фотони, які випромінюються лазером ЛГН-105, проходять через щілину, ширину якої Δх можна змінювати за допомогою мікрометричного гвинта. На екрані, розташованому на відстані L від щілини, спостерігається система дифракційних максимумів. Позначимо відстань між максимумами, які розташовані симетрично відносно головного максимуму, через d .
З рис. 1 маємо:
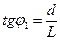 . (7)
. (7)
Тоді
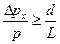 . (8)
. (8)
Отже
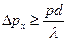 . (9)
. (9)
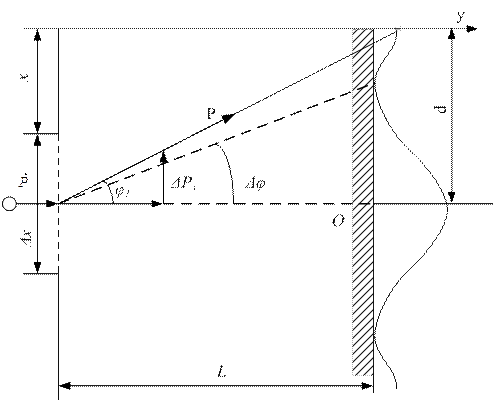
Рис. 1
Підставимо значення імпульсу з формули (1) і домножимо ліву і праву частину на Δх, одержимо
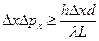 . (10)
. (10)
Зіставивши (10) з співвідношенням (6), переконуємося, що для виконання співвідношення невизначеностей необхідно, щоб виконувалась умова
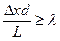 . (11)
. (11)
Таким чином, при виконанні умови (11) виконується також і умова (6). До перевірки нерівності (11) і зводиться дана робота.
Порядок виконання роботи
1. Розмістити щілину на осі пучка лазерного випромінювання.
2. Поставити перпендикулярно до пучка екран на відстані 0,4...0,5 м від щілини.
3. Змінюючи ширину щілини від 0,01 до 0,06 мм, виміряти значення d, що відповідають кожному значенню Δx.
4. Результати вимірювань занести в таблицю.
