Квантовый эффект Холла и новый эталон сопротивления

При изучении эффекта Холла в полевом транзисторе, помещенном в сильное магнитное поле, Клаус фон Клитцинг в 1980 г. обнаружил, что холловское сопротивление r_x = V_x/I_x, которое в условиях обычного эффекта Холла обратно пропорционально концентрации носителей заряда n, при изменении n то остается постоянным, то резко изменяется, переходя с одного уровня на другой [2]. Вместо монотонного убывания в зависимости r_x(n) наблюдались «ступеньки» — см. рис. 14.5.

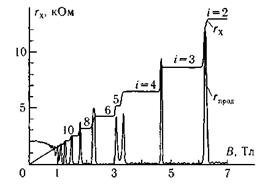
Рис. 14.5.

Холловское сопротивление на i-й ступеньке оказывается равным

r_x = h/(ie²), (14.11)

(i = 1, 2, 3, …- целое число), т. е. определяется такими фундаментальными константами, как постоянная Планка и заряд электрона, и не зависит от свойств вещества. Еще одним удивительным экспериментальным фактом оказалось практически полное исчезновение продольного сопротивления образца при тех же значениях внешнего магнитного поля, при котором r_x = соnst. Это новое физическое явление назвали квантовым эффектом Холла. На рис. 14.5, где изображен квантовый эффект Холла — плато в холловском сопротивлении, появляющиеся в сильных магнитных полях при низких температурах (~ 10 мК), — цифрами указаны номера уровней Ландау (о них речь ниже), на которых проявляется квантование. На этом же рисунке показано изменение продольного сопротивления с полем.

Рассмотрим качественно физическую картину квантового эффекта Холла. Прежде всего ознакомимся с устройством и принципом работы полевого транзистора [1].

Полевой транзистор — это транзистор, в котором управление протекающим через него током осуществляется электрическим полем, перпендикулярным направлению тока. Принцип работы полевого транзистора поясняется на рис. 14.6. Токовводы осуществляются через n-типа области на концах полупроводника с дырочным типом проводимости.

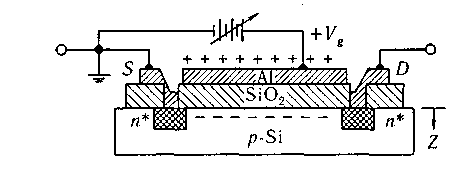
Рис. 14.6. Устройство полевого транзистора

Тонкая пластинка полупроводника (канал) снабжена двумя омическими электродами (истоком S и стоком D). Между истоком и стоком расположен третий электрод — затвор. Напряжение V_g, приложенное между затвором и любым из двух электродов, приводит к появлению «подзатворной» области канала электрического поля. Влияние этого поля приводит к изменению количества носителей заряда в канале вблизи затвора и, как следствие, изменяет сопротивление канала. Изготовляются полевые транзисторы главным образом из Si и GaAs. Как правило, в кремниевых полевых транзисторах монокристалл кремния, являющийся каналом транзистора, окисляется и образуется на его поверхности диэлектрический слой из SiO₂, на который наносится слой алюминия (затвор). Поэтому такие системы называются МДП-структурами (металл-диэлектрик-полупроводник). Область затвора представляет собой фактически конденсатор, в котором одной обкладкой служит металлический электрод затвора, а другой — канал полевого транзистора. Чем выше напряжение на затворе, тем более канал обогащается носителями тока. При этом электроны проводимости «поджимаются» полем затвора к границе раздела диэлектрик – полупроводник, образуя двумерное распределение электронного газа в приповерхностном слое полупроводника.

В поперечном к каналу направлении электроны двигаться практически не могут, они находятся в потенциальной яме, и их энергия может принимать только дискретные значения. При достаточно низкой температуре все они находятся на нижнем энергетическом уровне, что и приводит к строго двумерному электронному газу.

В плоскости канала энергия электронов не квантуется, однако при приложении перпендикулярно слою достаточно сильного внешнего магнитного поля электроны в плоскости начинают двигаться по круговым орбитам с циклотронной частотойD

w_c =еВ/m^*, (14.12)

где m^* - эффективная масса электрона.

Циклический характер движения электрона в магнитном поле является причиной того, что его энергия, связанная с движением в плоскости, перпендикулярной магнитному полю, становится дискретной величиной, или, как говорят, квантуется. Впервые это было показано Л.Д. Ландау в 1930 г. и поэтому называется квантованием Ландау. Круговое движение электронов подобно гармоническому осциллятору и поэтому энергия электронов может принимать лишь дискретные значения, определяемые, как известно, выражением

Е_n = (n + 1/2)ћw_c, (14.13)

где n – квантовое число; n = 0, 1, 2,….

Учет собственного магнитного момента электрона, связанного со спином для качественного рассмотрения эффекта не существеннен. Если температура образца достаточно низкая, т. е. расстояние между уровнями Ландау DE = ћw_c.>> k_БТ, то все электроны находятся в основном состоянии, соответствующем п = 0, и такое магнитное поле называется квантующим.

В квантующем поле все электроны оказываются в одном квантовом состоянии и поэтому, по принципу Паули, должны быть разнесены в пространстве, т. е. их орбиты не должны пересекаться. Это означает, что на каждом уровне Ландау может поместиться строго определенное число электронов.

Рассмотрим для простоты электроны на нулевом уровне Ландау. Радиусы орбит электронов можно определить, если учесть, что при круговом движении скорость электрона v = w_cr, и что его кинетическая энергия, как у любого гармонического осциллятора, равна половине полной энергии, т. е. тv²/2 = ћw_c/4. Из этих соотношений следует, что средний радиус кривизны траектории электрона в магнитном поле В равен

r = ћ/(2еВ), (14.14)

а соответствующая площадь орбиты

S = πr² = 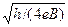. (14.15)

На самом деле у микроскопических объектов нет «точных» траекторий, волновая функция электрона «размазана» по пространству, и, как показывает точный расчет, эффективная площадь, соответствующая одному электрону, оказывается в 4 раза больше, т. е. электрон «заперт» на участке площадью S_эф= h/(еВ). Это означает, что на 1 см² поверхности можно разместить всего

N₀ = 1/S_эф = еВ/Н (14.16)

электронов в состоянии с n = 0, и, следовательно, при полностью заполненном нулевом уровне Ландау холловское сопротивление, согласно формуле (14.10), равно

r_H = U_H/I = B/(N₀e) = h/е² (14.17)

в полном соответствии с экспериментальными данными.

Из формулы (14.16) следует, что магнитный поток Ф, пронизывающий электронную орбиту, равен кванту магнитного потока Ф₀:

Ф = ВS = h/е = Ф₀. (14.18)

Другими словами, с каждым электроном связан точно один квант магнитного потока.

Существенной количественной характеристикой двумерной системы в магнитном поле является фактор заполнения ν, равный числу электронов в образце, деленному на число квантов магнитного потока, пронизывающих образец. Если ν равно целому числу i, то это означает, что i уровней Ландау полностью заполнены электронами, что и соответствует наличию плато в холловском сопротивлении.

Каждое заполненное состояние вносит вклад в проводимость, равный е²/h, и поэтому полная проводимость на i-м уровне оказывается равной iе²/h в полном согласии с экспериментом.

Для того чтобы понять, почему продольное сопротивление исчезает, вспомним, откуда оно вообще возникает. Причиной электрического сопротивления является рассеяние электронов на препятствиях — примесях, дефектах решетки. При рассеянии изменяется направление скорости электрона, т. е. изменяется его вклад в ток. Если на уровне Ландау есть свободные места, то такое рассеяние возможно. Другое дело, если уровень Ландау заполнен полностью. В этом случае все места на нем заняты и электрон не может изменить своего положения относительно других электронов. Единственная возможность изменить импульс в этом случае — это перейти на незаполненный следующий уровень Ландау, но это связано с существенным изменением энергии. Если ток идет по каналу, то ничто его не может затормозить, электроны перемещаются все вместе как единое целое, ни один электрон не может изменить свое состояние независимо от других, ему мешает это делать принцип Паули.

Остается понять, как формируются холловские плато, т. е. почему эти соотношения справедливы не только в выделенных точках, но и в некоей области значений В или N.

Пока мы показали лишь то, что при строго определенных соотношениях между концентрацией электронов n и величиной магнитного поля В становится равным нулю продольное сопротивление, и имеет строго определенное значение холловское сопротивление. Однако, как видно из рис. 5, экспериментально наблюдаются ступеньки (плато) в зависимости r_H(В), т. е. эти соотношения выполняются в конечном интервале значений В. Причиной появления плато является, как это ни кажется на первый взгляд парадоксальным, дефекты в МДП-структуре.

Дефекты приводят к изменению потенциального рельефа двумерного слоя, который становится похожим на пересеченную местность с впадинами, холмами и долинами. По долинам, соединяющим исток и сток, подобно реке, протекает ток, но многие эквипотенциали охватывают горы или ямы, и в них электроны застревают (становятся локализованными). При изменении магнитного поля, число электронов в дорожках увеличивается, но, как в реке, при этом расширяется поверхность токового канала, а концентрация электронов (их число на единицу поверхности) остается примерно неизменной. Этому постоянству плотности электронов способствует и локализация электронов в потенциальных ловушках. Дефекты создают для электронов резервуары, которые поддерживают постоянной плотность делокализованных электронов. Пока остается хотя бы одна дорожка, на которой концентрация точно равна i·n, весь ток будет течь по ней, т. к. ее сопротивление равно нулю и, следовательно, холловское напряжение меняться не будет. Но когда концентрация изменится, начнет заполняться следующий уровень Ландау и формироваться следующее холловское плато.

Квантованное холловское сопротивление h/е² сейчас измеряется с очень высокой точностью (до 10^―9), и равно 25812,806377 Ом. Эта точность оказалась выше, чем у эталонных сопротивлений. Поэтому с 1990 г. введена новая единица сопротивления — 1 клитцинг, определяемая как холловское сопротивление на четвертой ступеньке h/(4е²) = 6453,20159 Ом.

Итак, в квантовом эффекте Холла измеряется отношение двух фундаментальных констант — постоянной Планка и квадрата заряда электрона. Подобная комбинация входит в выражение для фундаментальной физической величины - постоянной тонкой структуры α = e²/(2e₀hc) = 1/137,0359895 (e₀ – электрическая постоянная в системе СИ) [3].

Тогда отношение h/е² можно записать в виде

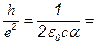×= 25812,8056(11) Ом. (14.19)

В последней формуле учтена экспериментальная погрешность в численном значении постоянной тонкой структуры. Мы видим, что измерение квантового холловского сопротивления действительно дает возможность с большой точностью определять значение постоянной тонкой структуры.

В 1985 г. Клаус Олаф фон Клитцинг (род. 1943 г.) получил Нобелевскую премию по физике за открытие квантового эффекта Холла. (О квантовом эффекте Холла см. книги [1—2] и нобелевскую лекцию К. фон Клитцинга [4].

В 1982 г. Д. Цуи, X. Штёрмер и А. Госсард обнаружили на кривой, изображающей зависимость холловского сопротивления от магнитного поля, при T = 0.5 К и В = 15 Тл новую ступеньку (плато) при i в формуле (14.11), равном 1/3. В дальнейшем наблюдались и другие плато при i = р/q при нечетных q (р, q - целые числа). Р. Лафлин нашел вариационные волновые функции многоэлектронных основного и возбужденного состояний, описывающие конденсацию электронного двухмерного газа в новое состояние вещества — двумерную электронную жидкость. Он предсказал существование возбуждений с дробными зарядами, подтвержденное впоследствии экспериментально. В 1998 г. Роберт Б. Лафлин (род. 1950 г.), Хорст Л. Штёрмер (род. 1949 г.) и Дэниэл Цуи (1939 г.) получили Нобелевскую премию по физике за открытие новой формы квантовой жидкости с дробно заряженными возбуждениями.

«Целочисленный квантовый эффект Холла» возникает как следствие замечательного проявления квантовой механики в условиях двухмерного пространства, в котором движутся электроны: плотность, с которой электроны заполняют двухмерную плоскость, может принимать только дискретные значения, пропорциональные величине магнитного поля, пронизывающего плоскость. Но оказалось, что заполнение с минимально возможной плотностью может быть не полным, например на 1/3. Это приводит к «дробному эффекту Холла». В экспериментах наблюдалось образование сгустков (или разреженностей) заряда в плоскости, заполненной на 1/3, которые проявляли себя как переносчики электрического заряда, равного 1/3 (или -1/3) заряда электрона. Возникновение «дробных» зарядов — это коллективный эффект, обязанный взаимодействию электронов друг с другом. «Расщепление электрона» [5], «Электрон разваливается на части» [6] — так назывались научно-популярные статьи о дробном квантовом эффекте Холла. Однако считать, что дробный квантовый эффект Холла означает, что электрон расщепляется, это примерно то же самое, что, основываясь на том, что человек живет в трехкомнатной квартире, утверждать, что в каждой комнате живет по одной трети человека, расщепленного на части. Оказалось, что возникновение дробных зарядов возможно и без дробления электронов. Появление квазичастиц с дробными зарядами — это удивительное и неожиданное следствие квантовой механики, описывающей поведение электронов в двухмерном пространстве. Исследования квантового эффекта Холла — замечательного макроскопического квантового явления — привели к более полному пониманию фундаментальных принципов квантовой теории. В своей нобелевской лекции [7] Р. Лафлин сказал, что открытие дробного квантового эффекта Холла — это глубокий и серьезный вызов привычному описанию Вселенной, редукционистскому сведению всего к «первым принципам», поскольку возможно, что все фундаментальные «выдающиеся проблемы в физике, включая квантовую, гравитацию, по сути, связаны именно с такими коллективными явлениями, которые нельзя вывести из свойств составляющих систему частей».

Контрольные вопросы

1. В чем заключается классический эффект Холла? Как он используется в измерительной практике?

2. Что такое квантовый эффект Холла?

3. Какие устройства используются для исследования и использования квантового эффекта Холла?

4. Как с помощью квантового эффекта Холла реализуется эталон электрического сопротивления? Чему равен один клитцинг?

5. Каков физический смысл постоянной тонкой структуры?

6. Что такое дробный квантовый эффект Холла?

Библиографический список

1. Курс физики: Учебник для вузов: В 2 т. Т. 1./ ред. В. Н. Лозовский. – СПб.: Лань, 2007. – § 2.41, 2.42.

2. Савельев, И.В. Курс общей физики в 3-х т. Т. 3 / И. В. Савельев. – М.: Наука, 2005. – § 79.

3. Трофимова, Т.И. Курс физики / Т.И. Трофимова. – М.: Высш. шк., 2001. – § 117.

4. Белонучкин, В.Е. Основы физики. Квантовая и статистическая физика. В 2 т. Т.2. / В.Е. Белонучкин, Д.А. Заикин, Ю.М. Ципенюк.– М.: ФИЗМАТЛИТ, 2001. – 504 с.

5. Квантовый эффект Холла. М.: Мир, 1989.

6. Фундаментальные проблемы теории точности / Под ред. В.П. Булатова, И.Г. Фридлендера. – СПб.: Наука, 2001. – 504 с.

7. Фон Клитцинг К. Квантовый эффект Холла // Успехи физических наук. 1986. Т. 150, вып. 1. С. 107—126.

8. Daviss B. Splitting the electron // New Scientist. 1998, 31 .January. Р. 36-40.

9. Anderson P.W. When the electron falls apart // Physics Today. 1997, October. Р. 42-47.

10. Лафлин Р. Б. Дробное квантование // Успехи физических наук. 2000, Т. 170, № 3. С. 292—301.