Описание установки и метода измерений. (вариант 2 –сравниваются теоретическое и экспериментальное значения момента инерции)

ИССЛЕДОВАНИЕ ОСНОВНОГО ЗАКОНА ДИНАМИКИ

ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ С ПОМОЩЬЮ МАЯТНИКА ОБЕРБЕКА

(вариант 2 –сравниваются теоретическое и экспериментальное значения момента инерции)

Цель работы: 1) определить момент инерции маятника эксперимен-тально; 2) рассчитать момент инерции маятника теоретически; 3) про-анализировать результат.

Приборы и принадлежности: маятник Обербека, набор грузов, секундо-мер, штангенциркуль, масштабная линейка.

Описание установки и метода измерений

Маятник Обербека, используемый в данной работе, изображен на рис. 5.1. Он состоит из двух шкивов различного радиуса R₁ и R₂, укрепленных на одной горизонтальной оси (на рисунке отмечена точкой), и четырех стержней, на которые надеваются одинаковые передвиж-ные грузы массой 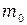.Грузы 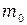могут быть закреплены на разных расстояниях 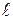от оси вращения маятника. На один из шкивов навивается нить, которая пере-брасывается через блок изменения направления движения нити. К свободному концу нити при-крепляется груз массой m, под действием которого маятник приво-дится во вращательное движение.

Рис. 5.1 Расстояние h, пройденное грузом за

время t,отмечается по вертикальной шкале.

Основной закон динамики вращательного движения в данной работе удобно записать в виде

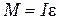, (5.1)

где 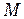– вращающий момент, действующий на маятник, 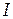– момент инерции маятника, 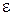– угловое ускорение маятника.

Формула (5.1) позволяет экспериментально найти момент инерции маятника. Для нахождения углового ускорения маятника будем считать, что нить нерастяжима, поэтому ускорение всех точек нити одинаково и равно ускорению любой точки поверхности шкива. Следовательно, угловое ускорение крестовины можно найти по формуле

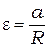, (5.2)

где 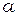– ускорение падающего груза, 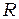– радиус шкива.

Ускорение груза можно найти, воспользовавшись уравнением равноускоренного движения

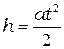, откуда 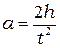. (5.3)

Вращение маятника происходит под действием моментов двух сил: силы натяжения нити и силы трения в подшипниках. Силу натяжения нити 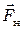находят, записав основной закон динамики для падающего груза (рис. 5.1):

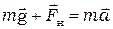
откуда, в скалярном виде ,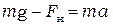

или 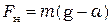. (5.4)

Если силой трения пренебречь и считать, что вращение крестовины происходит под действием только момента силы натяжения, то

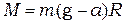, (5.5)

где 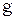– ускорение свободного падения.

Подставив в формулу (5.1) формулы (5.5) и (5.2), с учетом (5.3) получим выражение для расчета экспериментального значения момента инерции маятника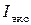

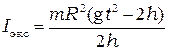. (5.6)

Теоретическое значение момента инерции маятника 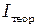рассчитывается как сумма моментов инерции составляющих его частей, то есть

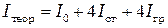, (5.7)

где 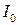– суммарный момент инерции двухступенчатого шкива и бобышки, на которой закреплены стержни, 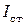– момент инерции одного стержня, 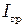– момент инерции подвижного груза.

Подставив в (5.7) выражения для 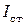и 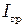, получим

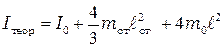, (5.8)

где 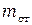– масса стержня, 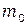– масса подвижного груза, 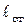– длина стержня, 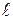– расстояние от центра масс грузов до оси вращения (так как размеры грузов малы по сравнению с расстоянием до оси вращения, их можно считать материальными точками).

Сравнив экспериментальное и теоретическое значения момента инерции маятника, делают вывод о выполнимости основного закона динамики вращательного движения. Для сравнения полученных значений необходимо рассчитать их погрешности.

Порядок выполнения работы

1. Закрепить грузы 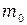на расстоянии 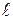от оси вращения маятника (указан-ном преподавателем), добившись его безразличного равновесия.

2. Определить пять раз время падения груза m.

3. Рассчитать экспериментальное и теоретическое значения момента инер-ции маятника при данном расположении грузов .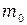

4. Результаты измерений и вычислений занести в таблицу

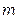№		R		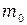	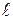t	< t>	h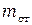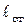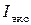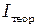

5. Рассчитать погрешности 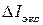по формуле (П.2), и 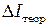– (П.7).

6. Убедиться в равенстве рассчитанных значений с учетом их погрешностей.

7. По предложению преподавателя повторить эксперимент, изменив массу груза 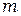или расстояние 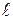, или то и другое одновременно.

Величины, считающиеся известными в данной работе:

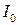= (0,0021 ± 0,0001) кгм², 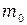= (200,0 ± 0,1) г,

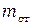= (62,0 ± 0,1) г, 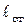= (27,0 ± 0,5) см.

Контрольные вопросы

1. Дайте определение момента инерции тела и поясните его физический смысл.

2. Дайте определение момента силы относительно оси.

3. Дайте определение угловой скорости, углового ускорения.

4. Поясните физический смысл векторных величин. Как они направлены? В каких единицах измеряются?

5. Сформулируйте теорему Штейнера. С ее помощью докажите, что в данной работе грузы 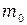можно считать материальными точками.

6. Запишите основной закон динамики вращательного движения в общем виде и для данной работы. Выведите формулу (5.6).

7. Выведите формулы для определения погрешностей рассчитанных значений.

Литература

1. Савельев И. В. Курс физики. Т. 1. – М.: Наука, 1989.– С. 94–116.

2. Трофимова Т. И. Курс физики. – М.: Высш. шк., 2001. С. 34–46.

3. Зисман Г. А., Тодес О. М. Курс обшей физики. Т.1. – М.: Наука,

1972. – С. 59–70.