Электропроводность твердых тел

Цель: экспериментально проверить закономерности изменения электропроводности в зависимости от температуры.

Теоретическая часть

Электрическое сопротивление. В 1827 г. Георг Ом исследовал зависимость силы тока в металлических проводах от приложенной разности потенциалов и установил их пропорциональность:

I = sU,

где I – сила тока, U – разность потенциалов между концами проводника, коэффициент пропорциональности s – проводимость проводника. На практике чаще пользуются обратной величиной 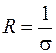, называемой сопротивлением проводника, и закон Ома записывается в виде:

.

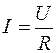В работах Ома было также выяснено, что сопротивление определяется геометрией проводника, его физико-химической природой и выражается формулой

,

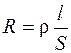где l – длина проводника, S – площадь сечения, r – удельное сопротивление, определяемое веществом проводника.

Природа электрического сопротивления. Для ее выяснения нам придется обратиться к микроскопической картине электрического тока, согласно которой ток представляет собой упорядоченное движение заряженных частиц – электронов и ионов, а сила тока определяется формулой

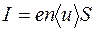, (64)

где е – заряд одного носителя, n – их концентрация, áuñ – средняя скорость их упорядоченного движения.

Для того чтобы в проводнике возник постоянный ток, необходимо создать в нем постоянное электрическое поле, т.е. приложить постоянную разность потенциалов (как следует из закона Ома). Носителями заряда в металлах и основными носителями в полупроводниках являются электроны. Постоянное электрическое поле будет действовать на них с постоянной силой F = eE и сообщать им постоянное ускорение 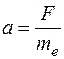(e и m_e – заряд и масса электрона). Тогда скорость электронов будет постоянно увеличиваться и через сечение проводника в единицу времени будет проходить всё большее число электронов, что означает увеличение силы тока. То есть мы пришли к противоречию с законом Ома. Следовательно, должен существовать какой-то механизм торможения, который объясняет наличие электрического сопротивления.

В классической электронной теории, предложенной Друде, считается, что электроны при своем движении сталкиваются с атомами (ионами) кристаллической решетки и при этом передают им всю кинетическую энергию упорядоченного движения. В промежутках между последовательными столкновениями электрон движется ускоренно, но после каждого столкновения скорость его упорядоченного движения равна нулю. В итоге такое скачкообразное движение можно рассматривать как равномерное со скоростью, равной средней скорости неравномерного. Разумеется, эти рассуждения являются достаточно упрощенными, но сущность их сохраняется во всех теоретических моделях: электрическое сопротивление обусловлено столкновениями носителей заряда с атомами решетки.

Отметим еще один важный момент. Атомы решетки при столкновении с электронами приобретают энергию, что соответствует повышению температуры кристалла. Иначе говоря, протекание тока в проводнике неизбежно сопровождается выделением тепла.

Температурный коэффициент сопротивления. Как показывает эксперимент, сопротивление металлов растет с повышением температуры. Вблизи комнатной температуры для большинства металлов и сплавов этот рост носит линейный характер:

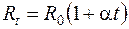, (65)

где t – температура по шкале Цельсия; R₀ и R_t – сопротивление при 0 °С и t °С; a – температурный коэффициент сопротивления. Для чистых металлов он оказался близок к 1/273 = 0,0367 град^-1.

У полупроводников сопротивление в области комнатных температур с увеличением температуры падает (в противоположность металлам) по экспоненциальному закону.

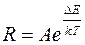, (66)

где А – некоторая константа; Т – абсолютная температура; k – постоянная Больцмана; DЕ называется энергией активации и представляет собой энергию, необходимую для перевода электрона из связанного состояния в свободное.

Выясним, почему сопротивление зависит от температуры. Начнем с металлов. С ростом температуры увеличиваются амплитуды колебаний атомов, в результате чего возрастает частота столкновений электронов с атомами решетки, а средняя скорость упорядоченного движения электронов падает. Тогда согласно (64) ток уменьшается, что означает увеличение сопротивления.

То же явление имеет место в полупроводниках, но в них с ростом температуры экспоненциально возрастает число свободных носителей заряда. Этот фактор превышает уменьшение средней скорости носителей, что обусловливает рост тока.

Экспериментальная часть

Схема установки представлена на рис. 40. Исследуемый образец 1 помещается в термостат 2. Температура в термостате измеряется термометром 3, задается положением реостата 5.

Сопротивление образца определяется прибором 4, в качестве которого могут использоваться: мост сопротивления МО-62, цифровой измеритель Р 5030, универсальный вольтметр В7-16 А или осциллограф мультиметр С1-112.

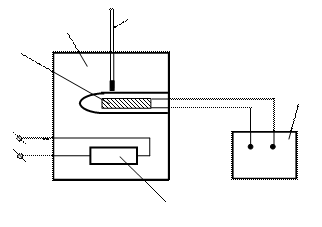Рис. 40

Порядок выполнения работы

Задание 1. Изучение зависимости сопротивления металлов от температуры.

1. Включить установку и произвести измерение сопротивления металлической проволоки через каждые пять градусов. Следует получить не менее десяти точек. Результаты измерения занести в табл. 14.

Таблица 14

t, °С	Т, К	1/Т, К-1	Сопротивление металла Rм Ом	Сопротивление полупроводника Rпп, Ом	ln Rпп

2. По полученным точкам построить зависимость R(t). Проверить, является ли она линейной. Результат проверки привести в выводе.

3. Как следует из (65), температурный коэффициент сопротивления вычисляется по формуле 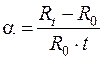. Вычислить a для трех значений температуры. Полученные значения усреднить, среднее сравнить с табличным. Результат сравнения описать в выводе.

4. Найти величину R₀ путем экстраполяции графика R(t) к 0 °С.

Результат привести в выводе.

Задание 2. Изучение зависимости сопротивления полупроводника.

Используется то же оборудование, что и в предыдущем эксперименте, только вместо металлической проволоки применяется термосопротивление. Измерения проводятся так же, как и в предыдущем опыте.

1. Построить зависимость R(t), начиная с самой низкой температуры, возможной в опыте.

2. Внести в таблицу значения lnR и 1/T.

3. Выбрать удобный масштаб и построить график lnR = f(1/T).

Примечание. Прологарифмировав (66), получим

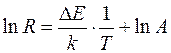. (67)

Отсюда видно, что зависимость 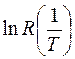является линейной. Поэтому, если полученный график – прямая, то результаты соответствуют формуле (66). Проанализировать полученный результат в выводе.

4. Определить энергию активации.

Примечание. Обозначив y = lnR и х = 1/Т, из (67) получим: dy/dx = DE/k. Следовательно, по известной dy/dx можно вычислить энергию активации DE. Поскольку график у(х) – прямая, то производную можно вычислить через конечные приращения по формуле j = Dу/Dх, т.е. DE= 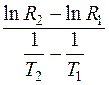, причем точки 1 и 2 выбираем по графику. Они должны лежать на прямой.

5. Сравнить полученное значение активации с табличными значениями для разных полупроводников. Результат сравнения привести в выводе.

Контрольные вопросы и задания

1. Запишите закон Ома. Поясните смысл входящих величин.

2. Какова природа электрического сопротивления?

3. Как сопротивление металла зависит от температуры?

4. Каковы основные положения классической теории электропроводности металлов?

5. Как проводимость полупроводников зависит от температуры?

Литература

1. Баулин В.И. Моделирование электростатических полей // Изучение некоторых тем в курсе физики: Сб. – Череповец, 1972.

2. Матвеев А.Н. Электричество и магнетизм: Учеб. для вузов. – М.: Наука, 1983.

3. Пичурин А.А. Методические рекомендации по выполнению лабораторных работ по электричеству: Учеб.-мет. пособие. – Череповец, 1991.

4. Калашников С.Г. Электричество: Учеб. для вузов. – М.: Наука, 1988.

5. Савельев И.В. Курс общей физики: Учеб. для вузов. – 3-е изд. – М.: Наука, 1988. – Т. 2–3.

6. Сивухин Д.В. Общий курс физики. Т. 3. Электричество: Учеб. для вузов. – М.: Наука, 1977.

7. Фриш С.Э., Тиморева А.В. Курс общей физики: Учеб. для вузов. – М.: Гос. изд-во физ-мат. литературы, 1962. – Т. ΙΙ.

8. Куликов К.А., Сидоренков Н.С. Планета Земля. – М.: Наука, 1972.

Оглавление

Введение ...................................................................................................... 3

Лабораторная работа 1. Исследование электростатического поля 3

Лабораторная работа 2. Определение емкости конденсатора методом мостика .......................................................................................................... 10

Лабораторная работа 3. Изучение закона Ома .................... 16

Лабораторная работа 4. Исследование работы источника постоянного тока ................................................................................................................ 25

Лабораторная работа 5. Измерение горизонтальной составляющей напряженности магнитного поля земли ...................................................... 31

Лабораторная работа 6. Измерение напряженности магнитного поля на оси катушки................................................................................................... 39

Лабораторная работа 7. Измерение индуктивности ............ 44

Лабораторная работа 8. Закон Ома для цепей переменного тока 50

Лабораторная работа 9. Измерение мощности в цепи переменного тока 61

Лабораторная работа 10. Изучение затухающих электромагнитных колебаний ............................................................................................................. 66

Лабораторная работа 11.Электропроводность твердых тел 72

Литература ................................................................................................ 78

Корректура: Г.В. Иванова

Изготовление оригинал-макета: М.Н. Авдюхова

Лицензия А № 165724 от 11.04.06 г.

Подписано к печати . Тир. .

Уч.-изд. л. 3,0. Усл. печ. л. 4,7. Формат 60 ´ 84 ¹/_16.

Гарнитура Таймс. Зак.

ФГБОУ ВПО «Череповецкий государственный университет»

162600, г. Череповец, пр. Луначарского, д. 5.