Матрица плотности

Если нет полной информации о системе, то она не имеет волновой функции и описывается матрицей плотности, введенной Ландау и Нейманом в 1927 г.

Лев Давидович Ландау Джон фон Нейман

(1908–1968) (1903–1957)

Чистое и смешанное состояния. Волновой функцией описывается чистое состояние. Для смешанного состояния известна лишь вероятность того, что состояние описывается одной из возможных волновых функций . Между этими функциями не определены фазовые соотношения и отсутствует интерференция. Например, если параметр системы измерен не точно, то состояние смешанное и является вероятностью i-ого значения параметра. Так, если в атоме водорода положение протона не фиксировано, то электрон находится в смешанном состоянии. Если протон неподвижен или его движение упорядочено, то состояние электрона чистое. Чистое состояние разлагается по ортонормированному базису с коэффициентами, которые могут регулярно изменяться. Если коэффициенты изменяются беспорядочно, то состояние смешанное. Чистое состояние переходит в смешанное в процессе декогеренциисистемы, когда она взаимодействует с объектом, испытывающим хаотические изменения, например, с макроскопическим телом. Декогеренция ускоряется с увеличением размеров квантовой системы, с ростом числа ее частиц, с увеличением температуры. Система в чистом состоянии должна быть изолирована от окружающих тел и хаотически меняющихся полей путем охлаждения, вакуумирования и экранирования. Уменьшение декогеренции необходимо для квантового компьютера, квантовой криптографии, квантовых коммуникаций. Смешанное состояние описывается матрицей плотности, чистое состояние – как волновой функцией, так и матрицей плотности.

Матрица плотности чистого состояния. Состояние 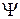разлагаем по собственным функциям некоторого эрмитового оператора 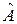с дискретным спектром

.

Состояние описываем набором коэффициентов . Для среднего значения величины a получаем

, (2.76)

где – матричный элемент оператора 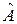между состояниями n и m.

Определяем матрицу плотности r с элементами

, (2.77)

тогда

, (2.78)

где

– шпур (от нем. die Spur – «след») – сумма диагональных элементов матрицы;

является вероятностью обнаружения состояния n в состоянии .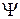

Пример. При общем количестве состояний

,

,

где

;

;

– вероятность результата .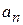

Наличие интерференционного слагаемого означает, что y₁ и y₂ в составе чистого состояния взаимно согласованы по фазе, т. е. когерентны, и их интерференция влияет на результат.

Матрица плотности смешанного состояния. Для смешанного состояния коэффициенты разложения зависят от не полностью определенного параметра состояния j, принимающего ряд значений. В (2.76) появляется дополнительное усреднение по j

,

где – вероятность j-ого значения. Определяем матрицу плотности в виде среднего по j

. (2.79)

Диагональный элемент матрицы плотности дает вероятность состояния

,

где является вероятностью состояния в компоненте j смешанного состояния. Недиагональные элементы (2.79) характеризуют корреляцию состояний m и n. Среднее значение (2.78) получает вид

.

При росте декогеренции и хаотизации фаз состояний происходит ослабление корреляции, недиагональные элементы матрицы плотности исчезают. Диагональные элементы переходят в распределение Больцмана по энергии.

Пример. При ,

.

Интерференционный член отсутствует, поэтому волновые функции компонент и смешанного состоянияне когерентные.

Свойства матрицы плотности. Выполняются:

Условие нормировки

. (2.80)

Условие эрмитовости

. (2.81)

Признак чистого состояния

. (2.82)

При нарушении (2.82) состояние смешанное.

Уравнение фон Неймана

(2.83)

является аналогом уравнения Шредингера для смешанного состояния.

Рассмотрим физические особенности поведения квантовой частицы, отличающие ее от классической частицы.