Свободные колебания в реальном контуре

Рассмотрим физические процессы в реальном контуре, состоящем из последовательно соединенных катушки индуктивности, конденсатора и некоторого активного сопротивления потерь 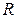. Сопротивление 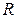эквивалентно омическому сопротивлению катушки индуктивности и сопротивлению потерь электрической энергии в конденсаторе.

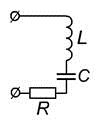
Рис. 3.11. Последовательный колебательный контур

Если зарядить однократно от внешней батареи конденсатор, то в контуре возникнет колебательный процесс. На основе второго закона Кирхгофа можно записать:

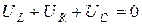. (3.55)

Или:

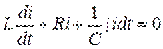(3.56)

Продифференцируем все слагаемые уравнения (2.55) по времени и разделим на :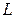

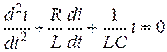(3.57)

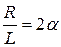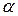Обозначим ,Где - коэффициент затухания.

Учитывая, что 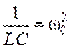, перепишем уравнение в следующем виде:

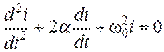(3.58)

Ищем решение этого уравнения в виде: .

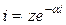Подставим это решение в уравнение:

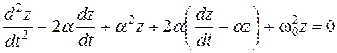(3.59)

Или:

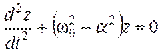,(3.60)

Где: .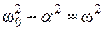

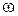- резонансная частота реального контура.

Решение последнего уравнения имеет вид:

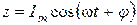(3.61)

Отсюда ток в контуре равен:

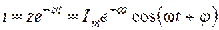.(3.62)

Полагая начальную фазу j=0, ток в контуре будет равен:

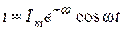(3.63)

Если a=0, то колебания не затухают. При этом:

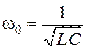(3.64)

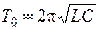(3.65)

В реальном контуре 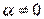, поэтому колебания на частоте 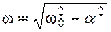Будут затухающими.

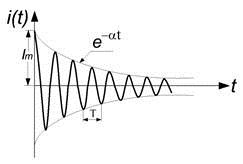
Рис. 3.12. Затухающие колебания в контуре с потерями

Период колебаний реального контура:

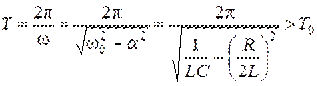(3.66)

Если 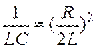, то период колебаний 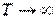. При этом колебательный процесс невозможен, а имеет место апериодический разряд конденсатора через катушку индуктивности и сопротивление потерь.

Колебательный процесс возможен только, когда 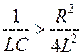или .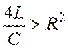

Отсюда: 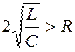или .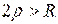

У радиотехнических контуров волновое сопротивление .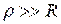

Поэтому с большой степенью точности можно считать, что период колебаний и резонансная частота в реальном контуре определяются следующими выражениями:

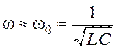(3.67)

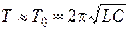(3.68)

По степени затухания колебательного процесса можно судить о качестве контура, которое оценивается добротностью:

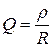(3.69)

Для радиотехнических контуров добротность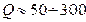

Добротность контура равна отношению напряжения на индуктивности 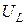или на емкости 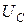к напряжению на активном сопротивлении при резонансе:

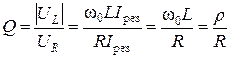(3.70)

В этом выражении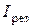 -Ток в контуре на резонансной частоте.

Умножим числитель и знаменатель на :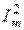

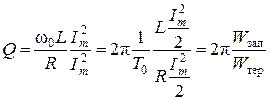. (3.71)

Добротность равна умноженному на 2 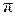отношению энергии, запасенной в контуре, к энергии, теряемой за один период колебаний.

Величина обратная добротности называется затуханием контура:

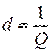. (3.72)

1. Фотоэлектрический эффект, законы внешнего фотоэффекта, уравнение Эйнштейна

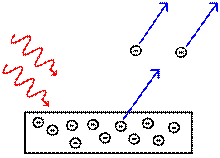
Фотоэффектом (или внешним фотоэффектом) называют испускание электронов поверхностью твёрдых или жидких тел под действием света. Фотоэффект, открытый немецким физиком Г. Герцем, можно наблюдать с помощью установки, показанной на рис. 30а. В стеклянную колбу Кпомещают два электрода (1 и 2) и создают вакуум, при этом через окошко О колбы на электрод 1 падает поток света. Свет, падающий на электрод 1, вырывает из его поверхности электроны (фотоэлектроны), движение которых зависит от электрического поля между электродами. Если напряжение U между электродами 1 и 2 (отсчитываемое от потенциала электрода 1) положительно, то фотоэлектроны полетят к электроду2, образуя ток (фототок), регистрируемый гальванометром Г.

Зависимость силы фототока I от напряжения U между электродами (см. чёрную кривую на рис. 30б) показывает, что при росте U сила фототока сначала увеличивается, а потом, достигая максимума, перестаёт расти. Максимальное значение силы фототока называют током насыщения I_н. Измеряя ток насыщения, можно вычислить, сколько фотоэлектронов каждую секунду вырываются из освещаемого электрода. При отрицательных U сила фототока уменьшается, т.к. электрическое поле тормозит фотоэлектроны, и до электрода 2 долетают только те, кинетическая энергия которых больше 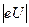. На рис.30б видно, что при напряжении, меньшем U_з, фототок отсутствует. U_З называютзапирающим (или задерживающим) напряжением и его величина следующим образом связана с максимальной кинетической энергией Е_максфотоэлектронов:

Е_макс = 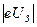. (30.1)

В опытах были установлены три закона фотоэффекта:

1. Сила фототока прямо пропорциональна плотности светового потока. Для сравнения на рис. 30б синей кривой показана зависимость фототока от напряжения для большей плотности светового потока.

2. Максимальная кинетическая энергия фотоэлектронов линейно растёт с частотой света (см. рис. 30в) и не зависит от плотности светового потока.

3. Для каждого вещества существует наименьшая частота света n_мин, ниже которой фотоэффект не происходит (см. n_минна рис. 30в), называемая красной границей фотоэффекта.

Законы фотоэффекта не удаётся объяснить с помощью законов классической физики, которую мы изучали до сих пор. Для их объяснения А. Эйнштейн в 1905 использовал идею, высказанную ранее немецким физиком М. Планком, согласно которой свет – поток частиц, фотонов. При этом энергия E каждого фотона, называемая квантом, равна:

E=hn, (30.2)

где n- частота света, а h – коэффициент, названный постоянной Планка и равный 6,63^.10^-34 Дж^.с.

Эйнштейн предположил, что фотон может выбить с поверхности только один электрон, а электрону, чтобы вырваться из вещества, необходимо совершить работу выхода А_вых. Тогда из закона сохранения энергии следовало, что при фотоэффекте энергия фотона hn должна быть равна сумме работы выхода А_вых и кинетической энергии фотоэлектрона со скоростью v и массой m:

В частности, максимальная начальная скорость электронов определяется из соотношения 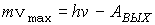, т.е зависит только от частоты v и материала катода (А_ВЫХ).

Красная граница v₀ соответствует v_max=0

hv₀=A_ВЫХ,v₀=A_ВЫХ/h (8)

При v>v₀ (или при l<l₀) фотоэффект наблюдается, при v<v₀ (или при l>l₀) - фотоэффект не наблюдается.