Вивчення руху мікрочастинки в потенціальній
Ямі КІНЦЕВОЇ глибини
16.1 Мета роботи
Дослідити рух мікрочастинки в потенціальній ямі кінцевої глибини, визначити власні значення енергії, власні хвильові функції мікрочастинки та ймовірність її знаходження в будь-якому інтервалі значень координат в потенціальної ямі та за її межами. Вивчити вплив обмеженості та асиметрії потенціальних бар’єрів на зазначені величини.
16.2 Вказівки з організації самостійної роботи
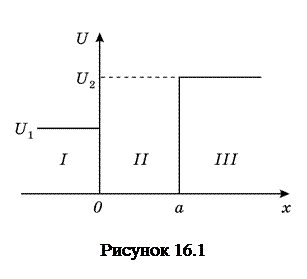
Потенціальна яма – це обмежена область простору, що визначається фізичною природою взаємодії частинок , в якій потенціальна енергія частинки менша, ніж за її межами (рис.16.1).
 Одновимірний рух частинки в стаціонарному силовому полі, яке характеризується потенціальною енергією U визначається стаціонарним рівнянням Шредінгера
Одновимірний рух частинки в стаціонарному силовому полі, яке характеризується потенціальною енергією U визначається стаціонарним рівнянням Шредінгера
|
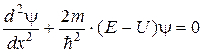 , (16.1)
, (16.1)
де m – маса частинки;
E – повна енергія частинки;
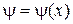 – псі-функція;
– псі-функція;
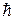 – стала Планка,
– стала Планка, 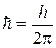 .
.
Для несиметричної одновимірної ями (рис.16.1) в області І ( 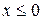 ) в рівнянні (16.1) необхідно покласти
) в рівнянні (16.1) необхідно покласти 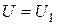 , в ІІІ (
, в ІІІ ( 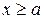 )
) 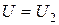 , та в області ІІ (
, та в області ІІ ( 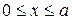 ) , для вільного руху U=0.
) , для вільного руху U=0.
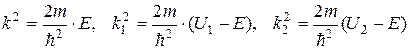 . (16.2)
. (16.2)
Вводячи позначення (для різних областей), отримуємо з рівняння (16.1) відповідно для областей І, ІІ, ІІІ рівняння:
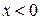 ,
, 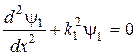 ; (16.3)
; (16.3)
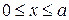 ,
, 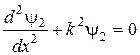 ; (16.4)
; (16.4)
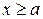 ,
, 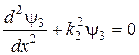 . (16.5)
. (16.5)
Розв’язок рівнянь (16.3), (16.4), (16.5) можна записати у вигляді
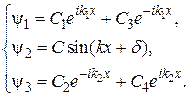 (16.6)
(16.6)
Всередині ями y-функція змінюється періодично (осцилює). За її межами, коли 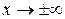 , щоб задовольнити умовам на нескінченності, необхідно покласти
, щоб задовольнити умовам на нескінченності, необхідно покласти 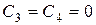 , бо нас цікавить випадок, коли частинка рухатиметься в межах ями. А це буде тоді, коли
, бо нас цікавить випадок, коли частинка рухатиметься в межах ями. А це буде тоді, коли 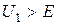 ,
, 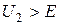 . За цих умов величини
. За цих умов величини 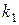 ,
, 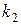 будуть уявними:
будуть уявними: 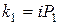
 ,
, 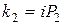 , і експоненти при коефіцієнтах наближатимуться до нескінченності (
, і експоненти при коефіцієнтах наближатимуться до нескінченності ( 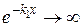 , коли
, коли 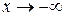 ;
; 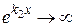 , коли
, коли 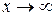 ).
).
На межах ями (х=0, х=а) y-функції та їх похідні мають задовольняти таким граничним умовам:
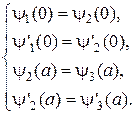 (16.7)
(16.7)
Якщо тепер підставити вирази y-функцій (16.6) (поклавши в них С3=С4=0) в граничні умови (16.7), можна отримати однорідну систему рівнянь, сумісний розв’язок якої врешті решт призведе до трансцендентного рівняння відносно хвильового числа k
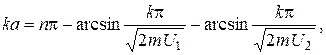 (16.8)
(16.8)
де п=1,2,3…,
а значення аrсsіn взято як головні значення. Корені рівняння (16.8) визначають дискретні рівні енергії 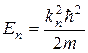 .
.
Для кожного значення n є один корінь, значення n нумерують корені в порядку їх зростання.
Обчислення коренів здійснюється за методом Ньютона. Припустимо, 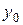 є наближене значення кореня рівняння
є наближене значення кореня рівняння 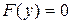 , тоді, як більш точне наближене значення таке:
, тоді, як більш точне наближене значення таке:
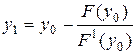 ,
, 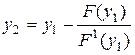 і т.д.
і т.д.
Як нульове наближення вибираємо значення в рівнянні (16.8) 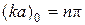 , що відповідає кореням рівняння для ями з нескінченно високими бар’єрами.
, що відповідає кореням рівняння для ями з нескінченно високими бар’єрами.
16.3 Опис комп’ютерної програми
Інтерфейс програми зображено на рис. 16.2. Програма видає на екран монітора: схему енергетичних рівнів електрона в несиметричній ямі, тобто в ямі, обмеженій потенціальними стінками різної “висоти” 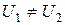 (в частинно-му випадку в симетричній ямі
(в частинно-му випадку в симетричній ямі 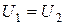 ); графік
); графік 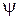 -функції, квадрата модуля
-функції, квадрата модуля 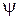 -функції
-функції 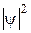 , ймовірність Р знаходження мікрочастинки в будь-якій області всередині ями та за її межами. Отримати відповідну інформацію можна, натиснувши мишкою на кнопки:
, ймовірність Р знаходження мікрочастинки в будь-якій області всередині ями та за її межами. Отримати відповідну інформацію можна, натиснувши мишкою на кнопки: 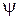 ,
, 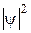 ,
, 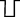 або Р. У відповідних вікнах можна змінювати значення
або Р. У відповідних вікнах можна змінювати значення 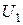 і
і 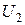 , ширини ями а, маси частинки m. За допомогою курсора можна встановлювати дві позначки в вибраних точках і обчислювати ймовірність Р знаходження частинки в області між цими точками. Змінюючи номер n
, ширини ями а, маси частинки m. За допомогою курсора можна встановлювати дві позначки в вибраних точках і обчислювати ймовірність Р знаходження частинки в області між цими точками. Змінюючи номер n 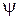 -функції можна отримувати графіки
-функції можна отримувати графіки 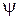 ,
, 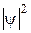 та значення Р для будь-якого значення n від 1 до
та значення Р для будь-якого значення n від 1 до 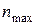 . Програма дає можливість проводити обчислення в широких межах зміни параметрів.
. Програма дає можливість проводити обчислення в широких межах зміни параметрів.
16.4 Інструкція користувачу
1. Задати значення а, 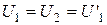 згідно з таблицею. Отримати на екрані схему рівнів енергії (синім кольором позначені рівні
згідно з таблицею. Отримати на екрані схему рівнів енергії (синім кольором позначені рівні 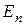 для ями з кінцевими бар’єрами, коричневим – рівні
для ями з кінцевими бар’єрами, коричневим – рівні 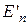 для ями з нескінченно високими бар’єрами). Збільшуючи U вдвічі, потім втричі, прослідкувати за зміною різниці
для ями з нескінченно високими бар’єрами). Збільшуючи U вдвічі, потім втричі, прослідкувати за зміною різниці 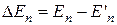 . Зробити висновок.
. Зробити висновок.
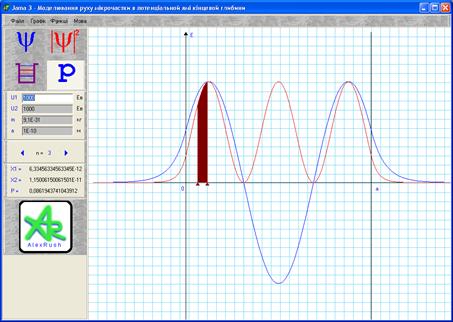
Рисунок 16.2
2. Для табличного значення 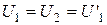 отримати на екрані графіки
отримати на екрані графіки 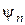 ,
, 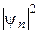 для значень п =1, 2, 3. Зарисувати ці графіки. Визначити формулу залежності кількості вузлів (нулів)
для значень п =1, 2, 3. Зарисувати ці графіки. Визначити формулу залежності кількості вузлів (нулів) 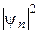 від номера п .
від номера п .
3. Збільшуючи U вдвічі, потім втричі (і більше) визначити ймовірність знаходження частинки в межах ями для п =1, 2, 3.
4. Задати значення 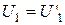 ,
, 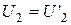 згідно з таблицею. Отримати та зарисувати графіки функцій
згідно з таблицею. Отримати та зарисувати графіки функцій 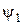 ,
, 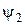 ,
, 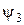 ,
, 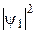 ,
, 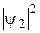 ,
, 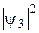 . Обчислити ймовірність знаходження частинки зліва та справа за межами ями. Змінюючи висоту одного з бар’єрів вдвічі, потім втричі, повторити обчислення ймовірностей для п=1, 2, 3. Зробити висновок, як впливає асиметрія ями на ймовірність проникнення частинки в бар’єр.
. Обчислити ймовірність знаходження частинки зліва та справа за межами ями. Змінюючи висоту одного з бар’єрів вдвічі, потім втричі, повторити обчислення ймовірностей для п=1, 2, 3. Зробити висновок, як впливає асиметрія ями на ймовірність проникнення частинки в бар’єр.
5. Встановити висоту бар’єрів 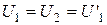 згідно з таблицею. Змінюючи масу частинки (
згідно з таблицею. Змінюючи масу частинки ( 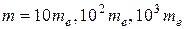 ), прослідкувати, як вона впливає на значення енергії
), прослідкувати, як вона впливає на значення енергії 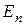 та різницю сусідніх значень
та різницю сусідніх значень 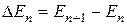 .
.
6. Повторити завдання (п=5), відновивши 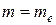 , змінюючи a в два, а потім у три рази.
, змінюючи a в два, а потім у три рази.
16.5 Зміст звіту
Звіт має містити: мету роботи, результати обчислення значень енергії
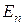 ,
, 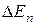 , ймовірностей (у вигляді таблиці), зарисовані графіки
, ймовірностей (у вигляді таблиці), зарисовані графіки 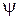 ,
, 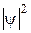 та висновки за пунктами роботи.
та висновки за пунктами роботи.
Таблиця 16.1 – Вихідні дані
| Номер вар. | 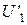 , eВ , eВ | а ∙10-10, м | 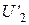 , eВ , eВ | Номер вар. | 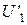 , eВ , eВ | а ∙10-10, м | 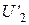 , eВ , eВ |
16.6 Контрольні запитання і завдання
1. Запишіть одновимірне стаціонарне рівняння Шредінгера, яке описує рух мікрочастинки в потенціальному полі.
2. Отримайте одновимірне стаціонарне рівняння Шредінгера для вільної частинки з рівняння (16.1).
3. Як запишеться стала розповсюдження k в різних областях простору та який вигляд відповідно прийме рівняння Шредінгера в цих областях?
4. Який вигляд має розв’язок ( 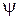 -функція) в різних областях?
-функція) в різних областях?
5. Як вестимуть себе 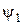 ,
, 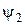 ,
, 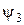 в ямі та за її межами у випадку, коли енергія частинки
в ямі та за її межами у випадку, коли енергія частинки 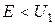 ,
, 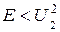 , наростатиме, загасатиме, осцилюватиме?
, наростатиме, загасатиме, осцилюватиме?
6. Яким граничним умовам має задовольняти ψ-функція та її похідна на межах ями?
7. Якого вигляду рівняння отримуємо для обчислення власних значень сталої розповсюдження k?
8. Який метод застосовується для розв’язання трансцедентного рівняння?
9. Як із рівняння (16.8) отримати відповідне рівняння для ями з нескінченно високими стінками?
10. Дайте визначення потенціальної ями.
11. Який фізичний зміст має 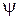 -функція (згідно з Бором)?
-функція (згідно з Бором)?
