Характеристики дискретного канала с помехами

При наличии помех в канале передачи информации нарушается однозначное соответствие между входными и выходными сигналами.

При передаче сигнала 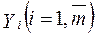возможен с различными вероятностями любой сигнал .

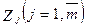Вероятностный характер связи между входными и выходными сигналами устанавливается матрицей переходных вероятностей

P₁₁ P₁₂......P_1m

P₂₁ P₂₂......P_2m

.............................

P_m1 P_m2.....P_mn ,

где P_ij - условная вероятность перехода i-ого символа входного алфавита в j-й символ выходного сигнала, при этом справедливо равенство .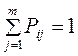

Дискретный канал, по которому передаются элементы, которые могут принимать только два значения (m=2) , называется бинарным (двоичным) дискретным каналом.

Матрица переходных вероятностей такого канала имеет вид:

P₁₁ P₁₂

P₂₁ P₂₂ .

Если вероятности правильной передачи различных элементов равны между собой P₁₁=P₂₂=p, а так же равны вероятности искажений P₁₂=P₂₁=q, то канал называется симметричным.

Дискретный симметричный канал (ДСК) имеет следующую матрицу переходных вероятностей

p q

p p.

В соответствии с (2.18) количество информации в условиях помех (когда передавался сигнал Y, а получен сигнал Z) определяется 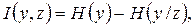или 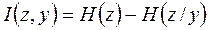, а скорость передачи информации будет

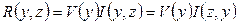. (3.7)

Максимальное значение R(y,z) определяет пропускную способность дискретного канала с помехами

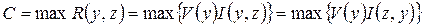. (3.8)

В данном случае максимальное значение R(y,z) зависит как от распределения вероятностей элементов, так и от величины помех в канале.

Определим пропускную способность дискретного симметричного канала ДСК. Для этого найдем составляющие выражения

.

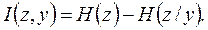Определим H(z) и H(z/y):

.

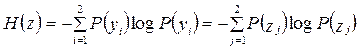Максимального значения эта величина достигает при равенстве вероятностей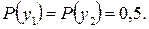

Тогда 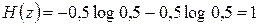[ дв.ед]

.

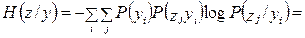
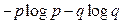В результате будем иметь

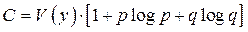. (3.9)

Это выражение для пропускной способности ДСК. Из выражения следует, что если элементы искажаются с вероятностью q=0.5, то пропускная способность равна 0. При q=0 (отсутствие ошибок в канале) C=V(y), т.е. пропускная способность будет определяться полосой пропускания канала.

Для дискретного канала с помехами доказана теорема Шеннона, в соответствии с которой вероятность искажения сообщений можно сделать сколь угодно малой при условии передачи сообщений со скоростями, не превышающими пропускной способности канала связи R<C .

Это достигается специальными методами помехоустойчивого кодирования сообщений, увеличивающими длительность блоков сообщений.

Обратное утверждение: если R>C, то передача со сколь угодно малой вероятностью ошибки невозможна.