Характеристики непрерывного канала с помехами

Под непрерывным каналом передачи информации принято понимать совокупность средств, обеспечивающих передачу непрерывных сигналов.

Однако определение скорости передачи информации и пропускной способности для данных каналов удобнее выполнить путем передачи дискретных отчетов по Котельникову.

В этом случае исходный сигнал y(t) будет иметь n=2F_kT отсчетов. После передачи отсчеты характеризуют сигнал Z(t), так как были подвергнуты искажениям.

В результате количество переданной информации на один отсчет определяется выражением (2.23) и может быть записано в следующей форме:

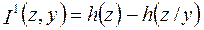. (3.10)

Общее количество (полное) информации будет

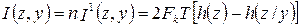. (3.11)

Тогда скорость передачи информации будет

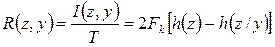. (3.12)

А пропускная способность непрерывного канала с помехами будет равна

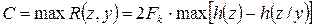(3.13)

Если в канале действует аддитивная помеха типа гауссова шума, то

пропускная способность канала определится выражением

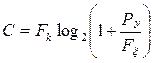, (3.14)

Р_y –средняя мощность сигнала,

Р_ξ – средняя мощность помехи.

Так как спектр помехи равномерен, то Р_ξ=Р₀ F_k.

Определим предел 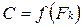при

.

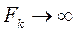
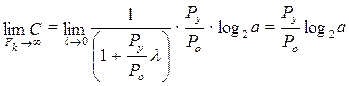Имеет смысл увеличивать F_k до величины порядка 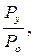так как далее сказывается насыщение.

Контрольные вопросы

1.Дать определение скорости передачи информации.

2.Дать определение пропускной способности ДСК без памяти.

3.Характеристики ДСК с помехами.

4.Сущность теоремы Шеннона для дискретного канала с помехами.

Эффективное кодирование информации

Понятие о кодировании

Коды появились в глубокой древности в виде, когда ими пользовались для засекречивания важного сообщения. В наше время коды приобрели иное значение, являясь, прежде всего, средством для экономной, удобной и практически безошибочной передачи сообщений. Новое применение кодов сложилось в результате бурного развития средств связи, неизмеримо возросшего объема передаваемой информации. Решать возникшие в связи с этим задачи было бы невозможно без привлечения самых разнообразных математических методов. Неслучайно поэтому теория кодирования считается сейчас одним из наиболее важных разделов прикладной математики.

Как известно, передача информации от источника к получателю производится посредством сигналов. Для того чтобы сигналы были однозначно поняты, их необходимо составлять по правилу, которое строго фиксировано в течение всего времени передачи данной группы сообщений. Правило, устанавливающее каждому конкретному сообщению строго определенную комбинацию различных символов, называется кодом, а процесс преобразования сообщения в комбинацию различных символов или соответствующих им сигналов - кодированием. Процесс восстановления содержания сообщения по данному коду называется декодированием.

Последовательность символов, которая в процессе кодирования присваивается каждому из множеств передаваемых сообщений, называется кодовым словом. Символы, с помощью которых записано передаваемое сообщение, составляют первичный алфавит, а символы, с помощью которых сообщение трансформируется в код - вторичный алфавит.

Исторически первый код, предназначенный для передачи сообщений, связан с именем изобретателя телеграфного аппарата Сэмюэля Морзе и известен всем как азбука Морзе. Другим кодом, столь же широко распространенным в телеграфии, является код Бодо. Оба они используют два различных элементарных сигнала. Такие коды принято называть двоичными.

Коды, в которых сообщения представлены комбинациями с неравным количеством символов, называются неравномерными, или некомплектными. Коды, в которых сообщения представлены комбинациями с равным количеством символов, называется равномерными, или комплектными.

Примером неравномерного кода может служить азбука Морзе, а равномерного - пятизначный код Бодо.

Коды могут быть представлены формулой, геометрической фигурой, таблицей, графом, многочленом, матрицей и.т.д.

Представление кода числа А в виде многочлена для любой позиционной системы счисления есть сумма произведений коэффициента а_i и веса x_i i-го разряда кода: .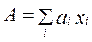

В качестве коэффициента 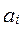используют целое неотрицательное число, причем 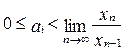,где 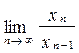- основание системы счисления.

Представление кода в виде геометрической модели возможно благодаря тому, что кодовые комбинации n-значного кода могут рассматриваться как определенные точки n-мерного пространства. Так, геометрическая модель двузначного кода представляет собой квадрат - фигуру двумерного пространства; трехзначного - куб (фигуру трехмерного пространства).