Систематический код Хемминга

Соотношение между числом информационных символов 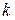, числом исправляемых ошибок 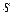и числом символов кодовой комбинации отображается неравенством (5.6). Хемминг предложил использовать знак равенства

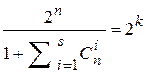. (5.15)

Таблица 5.2*
n
k
r
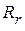	0.4286	0.2667	0.1613	0.0952	0.0551	0.0314

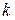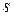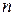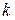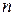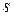Это предложение выполняется только для определённых соотношений , и . В таблице 5.2 приведены решения уравнения (5.15) для целых , и =1.

Коды 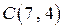имеют минимальное кодовое расстояние 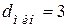и позволяют исправить одиночную ошибку. Коды 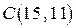имеют минимальное кодовое расстояние 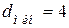, обнаруживают двукратную ошибку и позволяют исправить одиночную ошибку.

Второе предложение Хемминга касается построения проверочной матрицы [Березюк Справочник]. Проверочная матрица должна состоять из столбцов, являющихся кодом номера столбца в двоичном представлении. Например, для кода 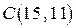проверочная матрица будет иметь вид

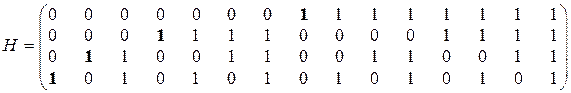В отличие от проверочной матрицы 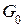, в которой проверочные символы занимают позиции после информационных символов, проверочные символы в матрице 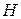занимают позиции кратные степени два 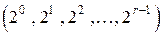и обозначены жирными единицами. Уравнения для определения проверочных символов получаются из матрицы 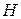, умножением его на вектор 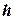, 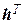=(h₁ ,h₂ , …, h₁₅ ):

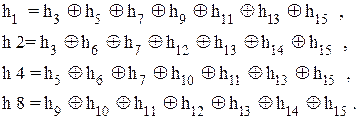(5.16)

Синдром ошибки составляется из проверочных символов и указывает номер позиции символа, в которой произошла ошибка. Если задана информационная часть кода 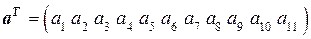, необходимо определить значения проверочных символов на 1-ой, 2-ой, 4-ой и 8-ой позициях пятнадцатиразрядного кода .

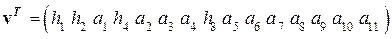Пример 5.3 Используем код 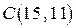с информационной частью

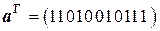. Составим таблицу 5.3, в первой строке – номера символов (разрядов) в кодовой комбинации, во второй – позиции проверочных и значения информационных символов.

Таблица 5.3

Номер символа

символы

h1

h 2

h 4

h 8

Подставим значения символов согласно таблице 5.3 в систему равенств (5.16) и получим значения проверочных символов h₁, h ₂ , h ₄, h ₈ .

h₁ = h₃ Å h₅ Å h₇ Å h₉ Å h₁₁ Å h₁₃ Å h₁₅ = 1 Å 1 Å 1 Å 0 Å 1 Å 1 Å 1 =0,

h ₂= h₃ Å h₆ Å h₇ Å h₁₂ Å h₁₃ Å h₁₄ Å h₁₅ = 1Å 0 Å 1 Å 0 Å 1 Å 1 Å 1 =1,

h ₄ = h ₅ Å h₆ Å h₇ Å h₁₀ Å h₁₁ Å h₁₃ Å h₁₅ = 1 Å 0 Å 1 Å 0 Å 1 Å 1 Å 1 =1,

h ₈ = h ₉ Å h ₁₀ Å h₁₁ Å h ₁₂ Å h₁₃ Å h ₁₄ Å h₁₅ = 0 Å 0 Å 1 Å 0 Å 1 Å 1 Å 1 = 0,

Кодер канала выдает последовательность символов

.

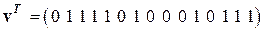Проверка правильности вычислений – произведение 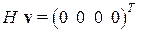. Если произошла однократная ошибка, скажем в третьем разряде, декодер выдает двоичный код ошибки 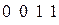, если ошибка в десятом разряде вектора, код ошибки равен .

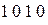Циклические коды

Циклические коды являются разновидностью систематических кодов. Они получили широкое распространение из-за простоты кодирования и декодирования. Все разрешённые кодовые комбинации производящей матрицы могут быть получены циклическим сдвигом одной разрешённой комбинации, называемой образующей для данного кода.

Любой 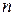-разрядный код можно представить в виде полинома степени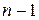

,

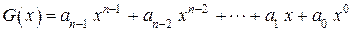где 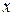- основание счисления,

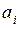- коэффициенты, принимающие значения «0» или «1», если .

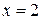Например, комбинацию 110101 можно записать как

.

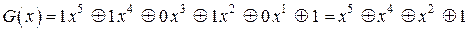Циклический сдвиг эквивалентен умножению многочле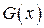на на .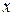

Действительно,

.

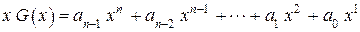Но в кодовой комбинации должно быть всего 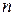членов, причём степень полинома не должна превышать 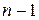. Чтобы удовлетворить этому условию, положим 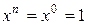. Тогда получим

,

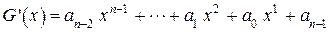т.е. получили циклический сдвиг. Если код, выраженный в виде полинома, принадлежит разрешённой кодовой комбинации, то кодовая комбинация, полученная циклическим сдвигом, также принадлежит разрешённой кодовой комбинации. Из условия того, что 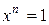имеем

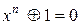. (5.16)

Пусть имеется полином 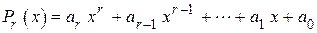степени 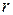. Среди полиномов 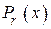выделим полиномы, которые делятся только лишь на самого себя и на 1. Такие полиномы называются простыми или неприводимыми.

Рассмотрим неприводимый полином 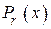и различные кодовые комбинации, выраженные в виде полиномов 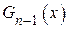степени 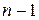. Из всей совокупности полиномов 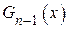к числу разрешённых кодовых комбинаций отнесём только те, которые делятся без остатка на полином 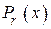. Определённый таким образом полином 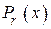степени 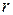называется образующим.

Циклическими 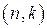кодами называются коды, каждая кодовая комбинация которых, выраженная в виде полинома, имеет степень, не превышающую 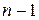, и нацело делится на образующий полином 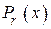степени .

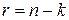Ввиду того, что циклические коды относятся к группе систематических кодов, то можно построить производящую матрицу.

Каноническая форма производящей матрицы 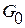размерности 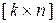(5.10) состоит из зеркального отражения единичной подматрицы размерности 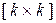, ( матрица отражения [Марпл]), и проверочной подматрицы размерности .

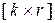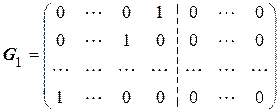. (5.23)

Каждую строку матрицы 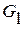разделим на неприводимый полином 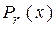, дающий n остатков, и заменим нули в соответствующей строке проверочной части матрицы на остаток 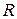. Результирующая матрица 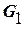будет производящей матрицей циклического кода .

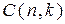Пример 5.5. Пусть n = 7, k = 4, r = 3. Первоначальное значение производящей матрицы имеет вид

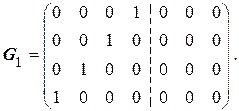Выберем образующий полином

Таблица 5.6
Номер строки
Код остатка

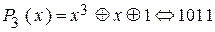, который дает 7 остатков при делении кода ошибки на образующий полином. Разделим коды строк производящей матрицы 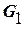на код образующего полинома 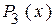. В результате имеем четыре остатка, значения которых приведены в таблице 5.6. После замены нулей в проверочной части матрицы соответствующими кодами остатков получим каноническую форму производящей матрицы

.

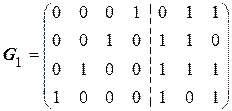Полученная производящая матрица состоит из четырёх строк (кодов). Все остальные 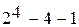=11 кодов, кроме кода 0000000, могут быть получены линейной комбинацией строк производящей матрицы .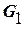