Элементы физики атомного ядра и ядерной физики 3 страница

3.54. Ток силой 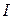= 50 А течет по проводнику, согнутому под прямым углом. Найти напряженность Н магнитного поля в точке, лежащей на биссектрисе этого угла на расстоянии 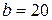см. Считать, что оба конца проводника находятся очень далеко от вершины угла.

3.55. По контуру в виде равностороннего треугольника течет ток силой 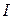= 50 А. Сторона треугольника 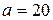см. Определить магнитную индукцию В в точке пересечения высот.

3.56. По двум параллельным проводам длиной 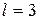мм каждый текут одинаковые токи силой 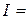500 А. Расстояние между проводниками 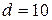см. Определить силу F взаимодействия проводников.

3.57. Бесконечно длинный прямой провод согнут под прямым углом. По проводу течет ток силой 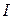= 100 А. Вычислить магнитную индукцию В в точках, лежащих на биссектрисе угла и удаленных от вершины угла на 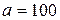см.

3.58. По бесконечно длинному прямому проводу, согнутому под углом 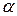= 120°, течет ток силой 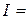50 А. Найти магнитную индукцию В в точках, лежащих на биссектрисе угла и удаленных от вершины его на расстояние 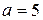см.

3.59. По контуру в виде квадрата идет ток силой 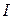= 50 А. Длина 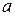стороны квадрата равна 20 см. Определить магнитную индукцию 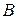в точке пересечения диагоналей.

3.60. По двум параллельным проводам длиной 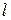=1 м каждый текут токи одинаковой силы. Расстояние d между проводами равно
1 см. Токи взаимодействуют с силой 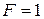мА. Найти силу тока 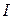в проводах.

3.61. По медному стержню массой т = 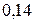кг, лежащему поперек двух рельсов, расположенных друг от друга на расстоянии 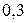м, проходит ток 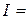50 А. Коэффициент трения скольжения по рельсам 0,6. Определить минимальную индукцию магнитного поля, при которой проводник начнет скользить по рельсам.

3.62. Проволочная прямоугольная рамка с током закреплена так, что может свободно вращаться вокруг горизонтально расположенной стороны а. Рамка находится в вертикальном однородном магнитном поле с индукцией В. Определить ток в рамке, если угол наклона рамки к горизонту 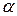. Масса провода а равна 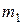, провода b - .

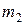3.63. Электрон движется в однородном магнитном поле с индукцией 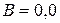1 Тл по окружности. Определить угловую скорость вращения электрона.

3.64. Электрон, обладая скоростью v = 10 Мм/с, влетел в однородное магнитное поле перпендикулярно линиям магнитной индукции. Индукция магнитного поля 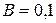Тл. Определить нормальное и тангенциальное ускорения электрона.

3.65. Протон, ускоренный разностью потенциалов 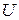= 0,5 кВ, влетая в однородное магнитное поле с магнитной индукцией 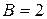мТл, движется по окружности. Определить радиус этой окружности.

3.66. Электрон, влетев в однородное магнитное поле с магнитной индукцией 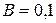мТл, движется по круговой орбите радиусом 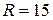см. Определить магнитный момент 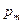эквивалентного кругового тока.

3.67. Электрон, обладая скоростью v = 1 Мм/с, влетает в однородное магнитное поле под углом 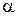= 60° к направлению поля и начинает двигаться по спирали. Напряженность магнитного поля
Н = 1,5 кА/м. Определить: 1) шаг спирали; 2) радиус витка спирали.

3.68. Кольцо из алюминиевого провода ( 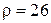нОм∙м) помещено в магнитное поле перпендикулярно линиям магнитной индукции. Диаметр кольца 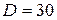см, диаметр провода 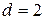мм. Определить скорость изменения магнитного поля, если ток в кольце 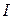= 1 А.

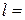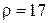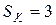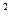3.69. В катушке длинной 0,5 м, диаметром d = 5 см и числом витков N = 1500 ток равномерно увеличивается на 0,2 А за одну секунду. На катушку надето кольцо из медной проволоки ( нОм∙м) площадью сечения мм . Определить силу тока в кольце.

3.70. В однородном магнитном поле ( 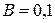Тл) вращается с постоянной угловой скоростью 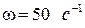вокруг вертикальной оси стержень длиной 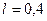м. Определить э.д.с. индукции, возникающей в стержне, если ось вращения проходит через конец стержня параллельно линиям магнитной индукции.

3.71. В однородном магнитном поле 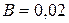Тл равномерно вращается вокруг вертикальной оси горизонтальный стержень длиной 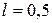м. Ось вращения проходит через конец стержня параллельно линиям магнитной индукции. Определить число оборотов в секунду, при котором на концах стержня возникает разность потенциало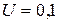в В.

3.72. Определить, сколько витков проволоки, вплотную прилегающихдруг кдругу, диаметром 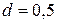мм с изоляцией ничтожной толщины надо намотать на картонный цилиндр диаметром 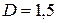см, чтобы получить однослойную катушку индуктивностью L = 100 мкГн?

3.73. Индуктивность соленоида при длине 1 м и площади поперечного сечения 20 см 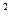равна 0,4 мГн. Определить силу тока в соленоиде, при которой объемная плотность энергии магнитного поля внутри соленоида равна 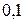Дж/м³.

3.74. Соленоид без сердечника с однослойной обмоткой из проволоки диаметром 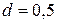мм имеет дайну 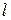= 0,4 и поперечное сечение 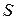= 50 см². Какой ток течет по обмотке при напряжении 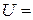10 Вт, если за время 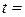0,5 мс в обмотке выделяется количество теплоты, равное энергии поля внутри соленоида? Поле считать однородным.

3.75. Обмотка электромагнита, находясь под постоянным напряжением, имеет сопротивление R = 15 Ом и индуктивность 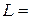0,3 Гн. Определить время, за которое в обмотке выделится количество теплоты, равное энергии магнитного поля в сердечнике.

3.76. Соленоид содержит 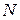= 1000 витков. Сила тока 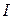в его обмотке равна 1 А, магнитный поток Fчерез поперечное сечение соленоида равен 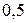мВб. Вычислить энергию 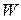магнитного поля.

3.77. На железное кольцо намотано в один слой 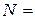200 витков. Определить энергию W магнитного поля, если при токе силы 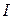=2,5 А магнитный поток Fв железе равен 0,5 мВб.

3.78. Обмотка тороида с немагнитным сердечником имеет 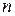= 10 витков на каждый сантиметр длины. Определить плотность энергии 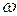поля, если по обмотке течет ток силой 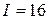А.

3.79. Сила тока 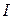в обмотке соленоида, содержащего 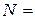1500 витков, равна 5 А. Магнитный поток Fчерез поперечное сечение соленоида составляет 200 мкВб. Определить энергию магнитного поля в соленоиде.

3.80. В соленоиде сечением 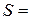5 см² создан магнитный поток F = 20 мкВб. Определить объемную плотность w энергии магнитного поля соленоида. Сердечник отсутствует. Магнитное поле во всем объеме соленоида считать однородном.

4.1. На мачте высотой h = 8 м висит лампа силой света 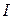= 1 кд. Принимая лампу за точечный источник света, определить, на каком расстоянии 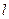от основания мачты освещенность Е поверхности земли равна 1 лк.

4.2. Над центром круглой площадки висит лампа. Освещенность 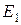в центре площадки равна 40 лк, Е₂на краю площадки равна 5 лк. Под каким углом i падают лучи на край площадки?

4.3. Вогнутое сферическое зеркало дает на экране изображение предмета, увеличенное в Г = 4 раза. Расстояние а от предмета до зеркала равно 25 см. Определить радиус R кривизны зеркала.

4.4. Фокусное расстояние F вогнутого зеркала равно 15 см. Зеркало дает действительное изображение предмета, уменьшенное в 3 раза. Определить расстояние а от предмета до зеркала.

4.5. Луч света падает на грань стеклянной призмы перпендикулярно ее поверхности и выходит из противоположной грани, отклонившись на угол 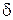= 25° от первоначально направления. Определить преломляющий угол 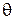призмы.

4.6. Пучок параллельных лучей падает на толстую стеклянную пластину под углом 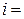60° и, преломляясь, переходит в стекло. Ширина а пучка в воздухе равна 10 см. Определить ширину b пучка в стекле.

4.7. Плосковыпуклая линза имеет оптическую силу 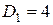дптр. Выпуклую поверхность линзы посеребрили. Найти оптическую силу D₂ такого сферического зеркала.

4.8. На горизонтальном дне бассейна глубиной 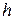= 1,5 м лежит плоское зеркало. Луч света входит в воду под углом 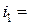45°. Определить расстояние s от места вхождения луча в воду до места выхода его на поверхность воды после отражения от зеркала. Показатель преломления воды 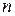= 1,33.

4.9. Двояковыпуклая линза с показателем преломления 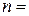1,5 имеет одинаковые радиусы кривизны поверхностей, равные 10 см. Изображение предмета с помощью этой линзы оказывается в 5 раз больше предмета. Определить расстояние от предмета до изображения.

4.10. Необходимо изготовить плосковыпуклую линзу с оптической силой D = 4 дптр. Определить радиус кривизны выпуклой поверхности линзы, если показатель преломления материала линзы равен 1,6.

4.11. Между стеклянной пластинкой и лежащей на ней плосковыпуклой линзой находится жидкость. Найти показатель преломления жидкости, если радиус 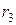третьего темного кольца Ньютона при наблюдении в отраженном свете с длиной волны 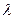= 0,6 мкм равен 0,82 мм. Радиус кривизны линзы 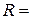0,5 м.

4.12. На тонкую пленку в направлении нормали к ее поверхности падает монохроматический свет с длиной волны 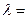500 нм. Отраженный от нее свет максимально усилен вследствие интерференции. Определить минимальную толщину 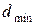пленки, если показатель преломления материала пленки п = 1,4.

4.13. На стеклянную пластинку положена выпуклой стороной плосковыпуклая линза. Сверху линза освещена монохроматическим светом длиной волны 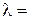500 нм. Найти радиус R линзы, если радиус четвертого кольца Ньютона в отраженном свете 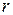= 2 мм.

4.14. На тонкий стеклянный клин падает нормально пучок лучей с длиной волны 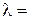500 нм. Расстояние между соседними темными интерференционными полосами в отраженном свете 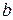= 0,5 мм. Определить угол aмежду поверхностями клина. Показатель преломления стекла, из которого изготовлен клин, п = 1,6.

4.15. Расстояние между двумя щелями в опыте Юнга 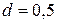мм ( 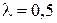мкм). Определить расстояние 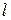от щелей до экрана, если ширина 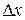интерференционных полос равна 1,2 мм.

4.16. На стеклянный клин (п = 1,5) нормально падает монохроматический свет ( 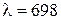нм). Определить угол между поверхностями клина, если расстояние между двумя соседними интерференционными максимумами в отраженном свете равно 0,2 мм.

4.17. На стеклянный клин ( 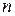= 1,5) нормально падает монохроматический свет. Угол клина равен 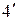. Определить длину световой волны, если расстояние между двумя соседними интерференционными максимумами в отраженном свете равно 0,2 мм.

4.18. На тонкую мыльную пленку ( 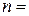1,33) под углом 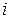= 30° падает монохроматический свет с длиной волны 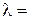0,6 мкм. Определить угол между поверхностями пленки, если расстояние b между интерференционными полосами в отраженном свете равно 4 мм.

4.19. Плосковыпуклая линза радиусом кривизны 4 м выпуклой стороной лежит на стеклянной пластинке. Определить длину волны падающего монохроматического света, если радиус пятого светлого кольца в отраженном свете равен 3 мм.

4.20. Плосковыпуклая линза с показателем преломления 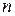= 1,6 выпуклой стороной лежит на стеклянной пластинке. Радиус третьего светлого кольца в отраженном свете ( 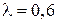мкм) равен 0,9 мм. Определить фокусное расстояние линзы.

4.21. Постоянная дифракционной решетки в п = 4 раза больше длины световой волны монохроматического света, нормально падающего на ее поверхность. Определить угол 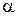между двумя первыми симметричными дифракционными максимумами.

4.22. На дифракционную решетку падает нормально параллельный пучок лучей белого света. Спектры третьего и четвертого порядков частично накладываются друг на друга. На какую длину волны в спектре четвертого порядка накладывается граница ( 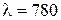нм) спектра третьего порядка?

4.23. На дифракционную решетку, содержащую 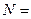600 штрихов на миллиметр, падает нормально белый свет. Спектр проектируется помещенной вблизи решетки линзой на экран. Определить длину 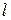спектра первого порядка на экране, если расстояние от линзы до экрана 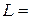12 м. Границы видимого света: 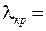780 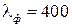нм, нм.

4.24. На грань кристалла каменной соли падает параллельный пучок рентгеновских лучей. Расстояние между атомными плоскостями кристалла 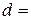280 пм. Под углом 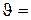65° к плоскости грани наблюдается дифракционный максимум первого порядка. Определить длину волны 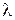рентгеновских лучей.

4.25. Определить радиус четвертой зоны Френеля, если радиус второй зоны Френеля для плоского волнового фронта равен 2 мм.

4.26. На щель шириной 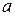= 0,1мм падает нормально монохроматический свет ( 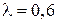мкм). Экран, на котором наблюдается дифракционная картина, расположен параллельно щели на расстоянии 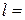1м. Определить расстояние 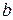между первыми дифракционными минимумами, расположенными по обе стороны центрального фраунгоферова максимума.

4.27. На щель шириной 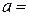0,1 мм падает нормально монохроматический свет с длиной волны 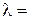0,5 мкм. Дифракционная картина наблюдается на экране, расположенном параллельно щели. Определить расстояние 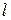от щели до экрана, если ширина центрального дифракционного максимума 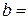1см.

4.28. На дифракционную решетку нормально падает монохроматический свет с длиной волны 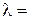0,5 мкм. На экран, находящийся от решетки на расстоянии 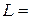1 м, с помощью линзы, расположенной вблизи решетки, проецируется дифракционная картина, причем первый главный максимум наблюдается на расстоянии 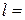15 см от центрального. Определить число штрихов на 1 см дифракционной решетки.

4.29.Узкий параллельный пучок рентгеновского излучения с длиной волны 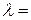245 пм падает на естественную грань монокристалла каменной соли. Определить расстояние d между атомными плоскостями монокристалла, если дифракционный максимум второго порядка наблюдается при падении излучения к поверхности монокристалла под углом скольжения.

4.30. Узкий параллельный пучок монохроматического рентгеновского излучения падает на грань кристалла с расстоянием d между его атомными плоскостями 0,3 нм. Определить длину волны рентгеновского излучения, если под углом 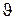= 30° к плоскости грани наблюдается дифракционный максимум первого порядка.

4.31. Луч света проходит через два николя, плоскости пропускания которых образуют между собой угол 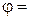40°. Принимая, что коэффициент поглощения 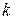каждого николя равен 0,15, найти, во сколько раз луч, выходящий из второго николя, ослаблен по сравнению с лучом, падающим на первый николь.

4.32. Угол падения 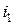луча на поверхность стекла равен 60°. При этом отраженный луч оказался максимально поляризованным. Определить угол i₂ преломления луча.

4.33. Угол 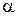между плоскостями пропускания поляроидов равен 50°. Естественный свет, проходя через такую систему, ослабляется 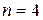раза. Пренебрегая потерей света при отражении, определить коэффициент поглощения 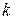света в поляроидах.

4.34. Луч света идущий в стеклянном сосуде с глицерином, отражается от дна сосуда. При каком угле падения 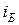отраженный луч максимально поляризован?

4.35. Пластинку кварца толщиной 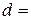2 мм поместили между параллельными николями, в результате чего плоскость поляризации монохроматического света повернулась на угол 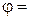53°. Какой наименьшей толщиной 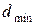следует взять пластинку, чтобы поле зрения поляриметра стало совершенно темным?

4.36. Определить, во сколько раз ослабится интенсивность света, прошедшего через два николя, расположенные так, что угол между их главными плоскостями 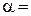60°, а в каждом из николей теряется 8% интенсивности падающего на него света.

4.37. Степень поляризации частично поляризованного света составляет 0,75. Определить отношение максимальной интенсивности света, пропускаемого анализатором, к минимальной интенсивности.

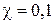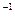4.38. Коэффициент поглощения некоторого вещества для монохроматического света определенной длины волны см . Определить толщину слоя вещества, которая необходима для ослабления света: 1) в 2 раза, 2) в 5 раз. Потери на отражение света не учитывать.

4.39. Определить концентрацию свободных электронов ионосферы, если для радиоволн с частотой 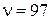МГц ее показатель преломления 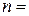0,91.

4.40. При прохождении в некотором веществе пути х интенсивность света уменьшилась в 3 раза. Определить, во сколько раз уменьшится интенсивность света при прохождении пути .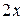

4.41. Температура абсолютно черного тела 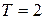кК. Определить длину волны 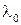, на которую приходится максимум энергии излучения, и спектральную плотность энергетической светимости (излучательности) 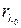для этой длины волны.

4.42. Определять температуру Т и энергетическую светимость (излучательность) 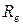абсолютно черного тела, если максимум энергии излучения приходится на длину волны 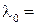600 нм.

4.43. Из смотрового окошечка печи излучается поток Ф_е=4 кДж/мин. Определить температуру 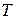печи, если площадь окошечка 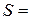8 см .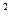

4.44. Поток излучения абсолютно черного тела Ф_е = 10 кВт, максимум энергии излучения приходится на длину волны 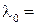0,8 мкм. Определить площадь S излучающей поверхности.

4.45. «Красная граница» фотоэффекта для цинка 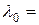310 нм. Определить максимальную кинетическую энергию 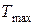фотоэлектронов в электрон-вольтах, если на цинк падают лучи с длиной волны 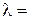200 нм.