Создание квантовой механики
Перед физикой стояла задача нахождения новых путей развития теории атомных явлений. Эти пути потребовали отказа от целого ряда понятий и давно установленных принципов.
Молодой немецкий ученый Гейзенберг установил основы так называемой матричной механики; французский физик де Бройль, а за ним австрийский физик Шредингер разработали волновую механику. Как вскоре оказалось, и матричная механика, и волновая механика — различные формы общей теории, получившей название квантовой механики.
К созданию матричной механики – одной из форм квантовой механики на первом этапе ее развития – Гейзенберг (1901—1975) пришел в результате исследований спектральных закономерностей, а также теории дисперсии. Квантовая теория дисперсии, развитая на основании теории Бора, уже не опиралась на модельные представления о строении атома. Если и можно говорить о модели атома в этой теории, то только лишь как о символической математической модели. В этой модели атом представлялся как совокупность виртуальных гармонических осцилляторов. Представления же об атоме как о системе, состоящей из ядра и вращающихся вокруг него электронов, которые обладают определенной массой, движутся с определенной скоростью по определенной траектории, нужно понимать лишь как аналогию для установления соответствующей математической модели. При этом особую роль играл принцип соответствия как принцип аналогии между классическим и квантовым рассмотрениями.
Указанный метод исследования развил Гейзенберг, распространив его вообще на теорию атомных явлений. Еще в 1923 году Гейзенберг принял точку зрения, согласно которой «модельные представления принципиально имеют только символический смысл, они являются классическими аналогами «дискретной» квантовой теории». Именно таким путем Гейзенберг рассчитывал преодолеть трудности, возникшие перед полуклассической теорией Бора. Теория атомных явлений, по Гейзенбергу, должна ограничиваться установлением соотношений между «наблюдаемыми» величинами, которые непосредственно измеряются в экспериментальных исследованиях – частотой излучения спектральных линий, их интенсивностью, поляризацией. «Ненаблюдаемые» же величины, такие, как координаты электрона, его скорость, траектория, по которой он движется, не должны использоваться в теории атома.
Однако в согласии с принципом соответствия новая теория должна определенным образом соответствовать классическим теориям. Конкретно это должно выражаться в том, что соотношения новой теории должны находиться в отношении аналогии с соотношениями классических величин. При этом каждой классической величине нужно найти соответствующую ей квантовую величину и, пользуясь классическими соотношениями, составить соответствующие им соотношения между найденными квантовыми величинами. Заменяя в уравнениях движения классические величины их квантовыми аналогами и используя квантовый аналог условия квантования, Гейзенберг получил уравнения, позволяющие определить излучаемые частоты и их интенсивности.
В 1925 году немецкие физики Борн и Иордан придали идеям Гейзенберга более строгую математическую форму. Они показали, что те величины, которые Гейзенберг поставил в соответствие классическим величинам, являются матрицами. В последующей работе совместно с Гейзенбергом, Борн и Иордан развивают математический аппарат матричной механики, применив его для решения ряда задач.
Независимо от Гейзенберга, Борна и Иордана английский физик Поль Антуан Морис Дирак (1902), познакомившись с теорией Гейзенберга, разработал для новой теории несколько иной математический аппарат. Дирак вводит в квантовую механику вместо матриц линейные дифференциальные операторы.
 Другое направление в развитии теории атома, основанное на других принципах, нежели те, на которые опирались Гейзенберг, Борн, Дирак и др., начало развиваться в работах французского физика Луи де Бройля (1892–1987), первые из которых были опубликованы в 1923 году. В них была высказана идея о волновой природе материальных частиц. Дальнейшее развитие эта идея получила в последующих работах де Бройля
Другое направление в развитии теории атома, основанное на других принципах, нежели те, на которые опирались Гейзенберг, Борн, Дирак и др., начало развиваться в работах французского физика Луи де Бройля (1892–1987), первые из которых были опубликованы в 1923 году. В них была высказана идея о волновой природе материальных частиц. Дальнейшее развитие эта идея получила в последующих работах де Бройля
На основании уже установленного факта наличия у света одновременно и корпускулярных и волновых свойств, а также оптико-механической аналогии у де Бройля возникла идея о существовании волновых свойств у частиц. Основные идеи де Бройля, высказанные им в его работах, сводятся к следующему. Так же как фотон, материальные частицы обладают корпускулярными и волновыми свойствами. Со всякой материальной частицей связан волновой процесс с частотой, которая определяется из соотношения Планка, а энергия частицы из соотношения Эйнштейна. Для длины волны получается выражение h/p, известное соотношение де Бройля.
Полученные для свободной частицы результаты де Бройль считает возможным распространить и на более общий случай движения частицы с переменной скоростью, т. е. на частицу, находящуюся в силовом поле. Теория де Бройля объясняет квантовые условия устойчивости круговых орбит, установленные Бором. Движение электрона по круговой орбите устойчиво только тогда, когда длина волны укладывается целое число раз на окружности, описываемой электроном.
Введя представление о волнах, связанных с движущейся частицей (они получили название волн де Бройля), де Бройль не дает определенного ответа на вопрос, что представляют собой эти волны, какова их природа? Он только подчеркивает, что это не обычные материальные волны, несущие энергию. Это следует из того, что их скорость больше скорости света, следовательно, их распространение не может быть распространением энергии того или иного вида. Сам де Бройль называет эти волны «фазовыми волнами».
Первые работы де Бройля, в которых высказывалась идея волн, связанных с материальными частицами, не обратили на себя серьезного, внимания со стороны большинства физиков-теоретиков. Интерес к идеям де Бройля проявил только Эйнштейн, который уже в 1925 году использовал результаты теории де Бройля в статической физике при построении статистик Бозе–Эйнштейна. Особенно сильное влияние идеи де Бройля оказали на австрийского физика Эрвина Шрёдингера (1887–1961), который увидел в них источник для создания новой атомной механики.
В 1926 году последовали работы Шрёдингера, в которых он, развивая идеи де Бройля, построил так называемую волновую механику. В первом сообщении Шрёдингера постановка вопроса носит довольно формальный характер. Он хочет заменить непонятные постулаты Бора о дискретных состояниях атома и правила квантования некоторыми положениями, в которых целочисленность получается естественным образом сама собой подобно тому, как сама по себе получается целочисленность числа узлов при рассмотрении колеблющейся струны. Исходя из известного в механике уравнения Гамильтона–Якоби и рассматривая некоторую вариационную задачу, он получает для атома водорода уравнение
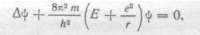
Оказывается, что это уравнение для случая Е < 0 имеет конечные, непрерывные и равные нулю на бесконечности решения только при определенных значениях. Таким образом, автоматически получается хорошо известное выражение для энергии дозволенных орбит, найденное Бором на основе выдвинутых им постулатов. Обсуждая полученные результаты, Шрёдингер подчеркивает, что пришел к ним под влиянием исследований де Бройля. Он указывает, что волновая функция естественным образом связана с неким колебательным процессом в атоме.
В следующем сообщении Шрёдингер уже не ограничивается формальной постановкой вопроса, а приводит рассуждения, оправдывающие полученное им уравнение. Возможно, что обычная механика является приближенной, справедливой только для обычных макропроцессов, и должна быть заменена для микропроцессов более точной механикой. В этом случае, распространяя оптико-механическую аналогию и опираясь на идеи де Бройля, можно предположить, что механика для микропроцессов должна иметь волновой характер. Продолжая рассуждать таким образом, Шрёдингер приходит к мысли, что механические процессы следует понимать или изображать как некие волновые процессы, характеризуемые волновой функцией. Тогда образ материальной точки, занимающей, например, определенное место в пространстве, строго говоря, является приближенным и может быть сохранен только при рассмотрении макропроцессов, подобно току, как мы пользуемся представлением о световом луче, которое теряет смысл, если рассматривать явления дифракции и интерференции.
Таким образом, получено уже известное из предыдущей статьи волновое уравнение Шрёдингера в общем виде. Шрёдингер ставит вопрос о связи его теории с теорией Гейзенберга, Борна и Иордана. Он высказывает мысль, что, несмотря на то что обе теории основываются на совершенно различных принципах, тем не менее между ними должно существовать связующее звено. В том же году в работе «О соотношении квантовой механики Гейзенберга, Борна, Иордана и моей» Шрёдингер впервые установил связь между квантовой и волновой механикой, которую уточнил в последующих работах. Он показал, что при всем различии исходных физических положений они математически эквивалентны. в последующих работах. Он показал, что при всем различии исходных физических положений они математически эквивалентны.
Успехи теории Шрёдингера сделали эту теорию весьма популярной. С одной стороны, с точки зрения математического формализма она была более удобна, нежели матричная механика. С другой стороны, казалось, во всяком случае сначала, что она дает возможность интерпретировать с понятной точки зрения закономерности атомной физики (без непонятных квантовых скачков, без отказа от наглядных представлений и т. д.). Однако многие теоретики и, прежде всего, Бор и основоположник матричной механики Гейзенберг, а также Дирак, возражали против шредингеровской интерпретации волновой функции.
Но если не принимать шредингеровскую интерпретацию волновой функции, то что следует понимать под этой функцией, какой физический смысл нужно ей придать, – на этот вопрос по-новому ответил Борн в 1926 году, предложив вероятностной толкование этой функции. По мнению Борна, волновая функция не представляет собой никакого реального физического поля, а имеет вероятностный смысл, подобно функции распределения, применяемой в статистической физике. К этой идее Борн пришел под влиянием замечания Эйнштейна о том, что двойственная природа света может быть просто понята, если принять, что амплитуда световых волн, а значит, и плотность энергии определяются средней плотностью фотонов в данной точке пространства. Распространяя эту идею на квантовую механику, Борн и предположил, что волновая функция также может иметь только статистический, вероятностный смысл. Статистическая интерпретация волновой функции, предложенная Борном, получила вскоре широкое признание и стала в основном общепринятой.
В 1927 году волновая механика получила новое прямое экспериментальное подтверждение. В этом году Дэвиссоном и Джермером было обнаружено явление дифракции электронов. Еще в 1921 году Рамзауер заметил, что при рассеянии электронов в газах наблюдается отклонение от результатов, предсказываемых классической теорией рассеяния частиц силовым центром. Дэвиссоном и Кунсменом в 1923 году было отмечено, что при рассеянии электронов на поверхности металла кривая рассеяния электронов по углам иногда имеет несколько более или менее выраженных максимумов, что не соответствовало теории. В 1925 году, после работ де Бройля, Эльзассер высказал мысль, что наблюдаемая аномалия является результатом волновой природы электрона и подтверждает гипотезу де Бройля. Однако к этой идее многие отнеслись прохладно, в том числе и сам Дэвиссон.
В 1927 году Дэвиссон совместно с Джермером производили новые опыты по рассеянию электронов на поверхности металлов. Для исправления случайной поломки им пришлось сильно прокалить установку. Произошла перекристаллизация, и вместо множества мелких кристаллов металла, от поверхности которых наблюдалось рассеяние электронов, образовалось несколько больших, и картина распределения рассеянных электронов по углам изменилась. Теперь уже не могло быть сомнений, что наблюдается явление дифракции электронов от кристаллической решетки, подобно дифракции рентгеновских лучей.
Вскоре явление дифракции электронов было обнаружено и исследовано рядом других физиков. Таким образом, гипотеза де Бройля получила прямое экспериментальное подтверждение, оказалось правильным и найденное им количественное соотношение для длин волн де Бройля. Кроме оправдания квантовой механики непосредственным подтверждением волновой природы электрона с помощью этой теории удалось построить более совершенную теорию твердого тела, теорию электропроводности, термоэлектрических явлений, теорию магнетизма и многое другое.
