Сформулируйте 2-ой закон Вина (дайте определение и запишите формулу)

Второй закон Вина: Максимальное значение спектральной плотности энергетической светимости абсолютно чёрного тела прямо пропорционально пятой степени абсолютной температуры.

r_max=С₂·Т⁵, где С₂ = 1,29·10^-5 Вт/м²·мК⁵

11. Запишите уравнение Эйнштейна для фотоэффекта

ε = hν = ħω = A_вых + Т_max

ε = A_вых +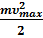

12. Сформулируйте гипотезу Планка (дайте определение и запишите формулу)

Атомы излучают энергию в виде порций – квантов, т.е. излучение носит дискретный характер.

Е = h 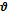= ħω

h = 6,62·10^-34 Дж·с, ħ = 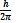- постоянная Планка

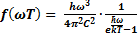– формула Планка.

13. Запишите выражение для энергии фотона

Е= hυ = ħω – энергия фотона.

14. Запишите выражение для импульса фотона

Р=(m 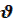)=E/C – импульс фотона.

15. Запишите закон сохранения энергии для эффекта Комптона

E + mc² = E^’+ mc² + T

16. Запишите закон сохранения импульса для эффекта Комптона

ħk = ħk^’ + p_e

17. Запишите выражение для длины волны смещённой компоненты излучения в эффекте Комптона

λ – λ₀ = λ_C(1-cosθ) = 2λ_Csin²(θ/2)

λ₀ - длина волны падающего излучения, λ - длина волны рассеянного излучения, λ_C - комптоновская длина волны, θ - угол рассеяния.

λ_C =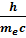

18. Сформулируйте корпускулярно-волновой дуализм

1) Почти монохроматическое излучение с частотой ω, испускаемое источником света, можно представить себе состоящим из «пакетов излучения», которые мы называем фотонами.

2) Распространение фотонов в пространстве правильно описывается классическими уравнениями Максвелла, при этом каждый фотон считается

классическим цугом волн, определённым двумя векторными полями E(r,t) и B(r,t).

3). Неправильно интерпретировать сумму квадратов амплитуд E и B как плотность энергии в пространстве, в котором движется фотон; вместо этого каждую величину, квадратично зависящую от амплитуды волны, следует интерпретировать как величину, пропорциональную вероятности какого-либо процесса.

4). Энергия, переданная в каком-либо месте пространства фотоном, всегда равна ħω. Тем самым

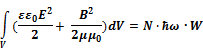
где W — вероятность нахождения фотона в данной области, а N — число фотонов.

19. Запишите выражение для спектрального терма водородоподобного атома

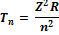
где R — постоянная Ридберга, а зарядовое число Z ядра введено ради удобства. Целое число n называется главным квантовым числом.

20. Запишите выражение для спектрального терма щелочных металлов

T(n) =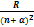

21. Запишите формулу Ридберга

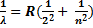, где R=1,1·10⁷

22. Запишите выражение для длины волны в серии Бальмера

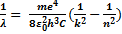, при k>2, n=3,4,..

np → 2s, ns → 2p, nd → 2p – серия Бальмера

23. Сформулируйте 1-й постулат Бора (дайте определение и запишите формулу)

Электрон в атоме водорода движется по круговым стационарным орбитам с постоянной скоростью под действием кулоновской силы в соответствии со вторым законом Ньютона. Разрешенными являются только те орбиты, на которых момент импульса электрона кратен ħ – постоянная Планка.

m 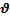r = nħ, n= 1,2,3…

24. Сформулируйте 2-й постулат Бора (дайте определение и запишите формулу)

Вращаясь по стационарным орбитам, электрон в атоме не излучает и не поглощает энергию, а излучает или поглощает энергию при переходе с одной стационарной орбиты на другую. Энергия излучения: hυ = E_n – E_m.

Если Е_m < E_n - то поглощает; Е_m > E_n – то излучает.

25. Запишите условие квантования Бора

L_n = mυr = nħ, n = 1,2,3…

26. Сформулируйте гипотезу де Бройля

Каждой движущейся частице, обладающей энергией Е и импульсом р, можно сопоставить волновой процесс, частота которого υ = Е/h, λ = h/p

а) Классический случай : 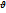<<C,T<<E₀, где Т – кинетическая энергия частицы. Тогда

Р = m 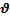, T = p²/2m → P =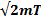

б) Если частица релятивистская: 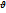~ С, Т ~ Е₀, где ~ - соизмерима, то

Р = m₀/( 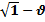²/C²)·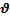

27. Запишите выражение для длины волны де Бройля нерелятивистской частицы

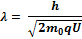
28. Запишите выражение для длины волны де Бройля релятивистской частицы

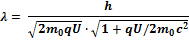
29. Запишите уравнение волны де Бройля

ψ(x,t)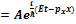

ψ(x,t) = Ae^-i/h(ωt-kr)

30. Сформулируйте физический смысл ψ-функции

Физический смысл волновой функции: Квадрат модуля волновой функции дает плотность вероятности обнаружить микрочастицу в данной точке пространства в данный момент времени.

ρ = 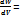|ψ|²

31. Сформулируйте основные свойства ψ-функции

1) Вероятностная интерпретация волновой функции |ψ(r)|² dV

2) Свойство непрерывности, однозначности и конечности ψ-функции

3) Условие нормировки ∫ψ² dV = 1

4) Ортогональность собственных функций

[E_n - E_m]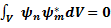

32. Сформулируйте условие нормировки для ψ-функции

Условие нормировки ∫ψ*ψ dV = 1

33. Запишите два соотношения неопределённостей Гейзенберга

Δx · Δp_x ≥ ħ – Произведение неопределенности координаты на неопределенность проекции соответствующего импульса не может быть меньше постоянной Планка с чертой.

ΔE · Δt ≥ ħ – Произведение неопределенности энергии микрочастицы на время пребывания микро частицы в данной квантовом соотношении не может быть меньше постоянной Планка с чертой.

34. Запишите уравнение Шрёдингера для частицы в одномерной потенциальной яме

ψ(x) =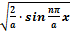

35. Запишите уравнение Шрёдингера для частицы в трёхмерной потенциальной яме

ψ(x,y,z,t) = A·sin 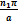x·B·sin 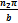y·C·sin 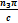z·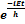

36. Запишите уравнение Шрёдингера для одномерного осциллятора

37. Запишите уравнение Шрёдингера для трёхмерного осциллятора

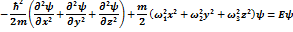
38. Запишите уравнение Шрёдингера для электрона в водородоподобном атоме

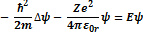
39. Сформулируйте принцип суперпозиции для квантовых состояний

ψ = a₁ψ₁ + a₂ψ_{2 ,} вероятность: |а₁|²,|а₂|²